Стационарное и равновесное состояния
Дав определения, связанные с понятием системы, перейдем к определению некоторых ее состояний, а именно — стационарного и равновесного.
Стационарным состоянием называется такое состояние системы, которое не изменяется во времени.
 |
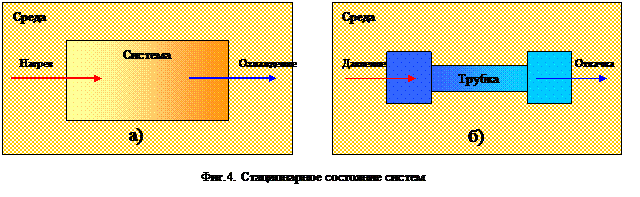Термодинамически равновесным, или просто равновесным, называется такое состояние, которое не изменяется во времени, причем эта неизменность не обусловлена протеканием какого-либо внешнего по отношению к системе процесса (равновесное состояние является частным случаем стационарного состояния той или иной системы). При стационарном состоянии температура и давление сохраняют постоянное значение. При равновесном состоянии эти величины не только постоянны, но одинаковы во всех точках системы. Сказанное поясним примером. Представим в качестве системы некий объем вещества (фиг. 4а), с одной стороны который мы нагреваем до определенной температуры, а с другой — охлаждаем, также до определенной температуры. В какой-то момент времени противоположные процессы (нагревание одного конца и охлаждение другого) приведут к установлению стационарного состояния, но не равновесного, так как постоянство параметров системы в каждой точке в данном случае поддерживается внешним по отношению к нашей системе процессом.
Система окажется в равновесном состоянии только тогда, когда во всех точках системы будет одна и та же температура и если такова же будет температура в окружающей среде (фиг.5). То же касается и давления. В равновесном состоянии система имеет наиболее низкий энергетический уровень.
|
|
|
Термодинамическому равновесию можно дать и несколько иное определение. Вообразим стержень с концами, нагретыми до определенных, но разных температур. В любой точке этого стержня температура будет иметь вполне определенное и постоянное значение. Однако тепловое состояние этого стержня характеризуется не одной температурой, а, строго говоря, бесконечным числом температур, так как каждая точка стержня будет иметь свою температуру, промежуточную между температурами его концов. Другой пример: вообразим трубку (фиг.4б), соединяющую два резервуара с одним и тем же газом, причем в этих резервуарах давление газа различное; постоянство давления в каждом резервуаре поддерживается работой насоса. В этом случае по трубке будет протекать газ. Здесь, как и в первом примере, нельзя говорить о равновесии, хотя можно говорить о стационарном состоянии, так как состояние системы может сохраняться сколь угодно долго, но это постоянство поддерживается в первом примере нагреванием и охлаждением концов, во втором — работой насосов. В последнем примере состояние системы характеризуется не одним давлением, а бесконечным числом давлений: двумя крайними в концах трубки и всеми промежуточными, причем в каждой точке давление остается постоянным.
|
|
|
Приведенные выше примеры ясно показывают, какие дополнительные требования надо предъявить к стационарному состоянию, чтобы его можно было считать равновесным. Стационарное состояние может характеризоваться бесконечным числом температур или давлений, лишь бы в каждой точке они оставались постоянными. При равновесном же состоянии системы температура и давление не только остаются постоянными в любой точке системы, но и должны быть одними и теми же для всех точек системы.
Выше были приведены примеры простейших систем, состояние которых характеризуется температурой и давлением. В более сложных системах приходится учитывать значения еще некоторых величин. Например, если мы имеем дело с растворами, то для определения их состояния необходимо, кроме температуры и давления, указать еще концентрации растворенных веществ. Все эти величины, характеризующие состояние системы, называются параметрами состояния. Теперь можем определить равновесное состояние как состояние, определяющееся конечным числом остающихся постоянными во времени параметров. При стационарном состоянии системы число таких параметров может быть, вообще говоря, бесконечным (бесконечное число давлений, температур и т. д.).
|
|
|
Нередко в системе устанавливается равновесное состояние в результате того, что скорости двух идущих в ней противоположных процессов становятся равными друг другу. Или в общей форме: характер одновременно протекающих процессов таков, что в конечном результате они компенсируют друг друга и скорость суммарного процесса оказывается равной нулю. Такое равновесие носит название динамического, или подвижного.
Системы подразделяются на стабильные (устойчивые), метастабильные и нестабильные (неустойчивые). Стабильная, или устойчивая, система—это система, находящаяся в равновесии, в то время как метастабильная система может казаться равновесной, но в действительности она не отвечает своему наиболее низкому энергетическому уровню. Большинство из наиболее плотных минералов, таких, как алмаз, кианит, жадеит, коусит, действительно стабильны только при высоких давлениях, однако они существуют метастабильно при низких давлениях и температурах в условиях земной поверхности, так как скорости реакций в этих условиях чрезвычайно малы. Подобным же образом многие минералы, образованные при высоких температурах, например санидин или кристобалит, метастабильны при комнатной температуре. Нестабильный минерал или минеральная ассоциация находятся в процессе перехода в более стабильное состояние.
Принцип Ле-Шателье
Дата добавления: 2018-08-06; просмотров: 3629; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!