МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (БИСЕКЦИИ) ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Дано уравнение

f(x) = 0,

где f(x) определена и непрерывна в некотором конечном или бесконечном интервале a≤x≤b. 

Пусть требуется найти корень уравнения (1) с заданной точностью ε > 0. Отрезок локализации [a, b], содержащий только один корень, будем считать заданным. Предположим, что f(x) непрерывна на [a, b] и f(x)f(x) < 0.

Разделим отрезок [a, b] пополам точкой с = (a + b)/2. Если f(c) ≠ 0, то возможны два случая:

1) функция f(x) меняет знак на отрезке [a, c];

2) функция f(x) меняет знак на отрезке [c, b].

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

На практике процесс прекращается, когда длина отрезка L = (b – a), полученная на очередной итерации, становится меньше заданной погрешности ε:

L ≤ ε.

В качестве корня берется величина

х = (b+a)/2.

Положительные стороны метода:

· всегда сходится («абсолютно застрахован от неудачи»).

Отрицательные стороны метода:

· довольно медленный;

· не обобщается на системы уравнений.

МЕТОД СЕКУЩИХ ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В ГРАФИЧЕСКОЙ ИНТЕРПРЕТАЦИИ

Если итерации x_n и x_n_-1 расположены достаточно близко друг к другу, то производную f’(x_n) в алгоритме Ньютона можно заменить ее приближенным значением

Таким образом, из формулы метода Ньютона получим формулу секущих

Геометрический смысл такого изменения алгоритма Ньютона состоит в том, что от аппроксимации f(x_n) касательной мы переходим к секущей – прямой, проходящей через 2 точки.

Замечание 1.Здесь в начале итерационного процесса задаются две точки x₁ и x₀.

Замечание 2.Условия сходимости метода и критерий окончания итерационного процесса те же, что и в методе Ньютона.

Замечание 3.Метод секущих также уступает методу Ньютона в скорости сходимости, однако не требует вычисления производной.

МЕТОД КАСАТЕЛЬНЫХ (НЬЮТОНА) ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В ГРАФИЧЕСКОЙ ИНТЕРПРЕТАЦИИ

Предположим, на отрезке [a, b] расположен один корень, который необходимо уточнить с точностью ε.

Пусть задано начальное приближение х₀ Є [a, b]. Расчетная формула метода Ньютона:

Если

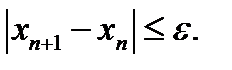
то значение х_n₊₁ считается приближенным значением корня уравнения.

Выражение для метода Ньютона получается из разложения функции f(x) в ряд Тейлора в окрестности точки х_n. Ограничиваясь двумя членами ряда, получим

Отсюда, полагая f(x) = 0 и решая полученное уравнение относительно x, получим

При замене х на х_n получается расчетная формула для метода Ньютона.

Геометрическая иллюстрация

Уравнение касательной к кривой в точке {x_n, f(x_n)}

Полагая, {у = 0, х = x_n₊₁}, получаем расчетную формулу.

Теорема 2.Если f(a) f(b) < 0, причем f’(x) и f’’(x) отличны от нуля и не меняют знак на отрезке [a, b], то при любом начальном приближении х₀ Є [a, b], удовлетворяющем условию  f(x₀) f’’(x₀) > 0, (т.е. знаки функции и второй производной в точке х₀ совпадают на интервале [a, b]) итерационный процесс сходится к корню уравнения f(x) = 0 с любой заданной точностью.

Замечание 1.Формула для метода касательных справедлива и для комплексных корней.

Замечание 2.Скорость сходимости выше, чем у других методов.

Замечание 3.В общем случае критерий окончания итерационного процесса не гарантирует, что с той же точностью совпадет x_n и x*. Поэтому целесообразно дополнительно проверять также условие | f(x_n) | < ε_f.

Дата добавления: 2018-08-06; просмотров: 300; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 9 Следующая ⇒

Мы поможем в написании ваших работ!