ОСНОВНЫЕ ДЕЙСТВИЯ С МАТРИЦАМИ

ВВЕДЕНИЕ В КУРС «МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭЛЕКТРОЭНЕРГЕТИКИ»

В настоящее время практически любой процесс может быть описан математическими соотношениями, в том числе и процессы, происходящие в электроэнергетических системах. Принимая некоторые допущения, можно сформировать математическую модель электрической системы любой сложности. При этом результаты расчетов таких моделей получаются достаточно точными.

Чтобы дать математическое описание электрической системы, надо в виде математической модели представить все связи между переменными величинами процессов. Изучение этих процессов, включая их математическую интерпретацию, направленно на обеспечение лучшей работы этой системы, основная задача которой – выработка электроэнергии.

Электроэнергия – это количественный показатель работы энергосистемы. Качество электроэнергии в основном характеризуется величинами напряжения и частоты у потребителя. Режим системы – это ее состояние в любой момент времени или на определенном интервале времени. Параметры режима – показатели, зависящие от изменения режима: напряжение; частота; токи; мощности и т.д.

При анализе и составлении математического описания различают три основных вида режимов электрических систем:

· нормальный установившийся режим, применительно к которому проектируется электрическая система и определяются технико-экономические характеристики;

· послеаварийный установившийся режим, наступающий после аварийного отключения какого-либо элемента или ряда элементов системы;

· переходный режим, во время которого система переходит от одного состояния к другому.

Связи между параметрами как нормального, так и послеаварийного установившихся режимов представляются алгебраическими уравнениями, т.к. параметры в таких режимах не изменяются. Для переходных режимов характерно изменение всех параметров режима, поэтому их необходимо описывать, используя дифференциальные уравнения.

Далее рассмотрим подробнее способы описания моделей и проведение математических расчетов применительно к электроэнергетическим системам. Но для начала вспомним из курса математики теорию матричного исчисления.

ФОРМЫ ЗАПИСИ СИСТЕМЫ ЛИНЕЙНЫЙ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)

В электроэнергетике основные расчеты режимов производят по первому и второму законам Кирхгофа, которые представляются в виде системы линейных алгебраических уравнений (СЛАУ). СЛАУ можно представить следующим образом

1) в развернутой форме

2) в компонентной форме

3) в матричной форме

ТИПЫ МАТРИЦ

Матрица – это прямоугольная таблица, имеющая определенное количество строк и столбцов. Строки нумеруются сверху вниз, столбцы – справа налево. На пересечении i-той строки и j-того столбца стоят элементы матрицы. Элементы матрицы могут быть представлены действительными или комплексными числами, символьными переменными, функциями времени, другой матрицей.

Различают следующиевиды матриц:

1. Прямоугольная матрица – количество строк и столбцов матрицы не совпадает (i ≠ j).

2. Квадратная матрица – частный случай прямоугольной матрицы, количество строк и столбцов матрицы одинаково (i = j).

3. Матрица (вектор) строка – количество строк матрицы равно единице, количество столбцов больше единицы (i = 1, j >1).

4. Матрица (вектор) столбец – количество столбцов матрицы равно единице, количество строк больше единицы (i > 1, j =1).

5. Нулевая матрица – все элементы матрицы равны нулю.

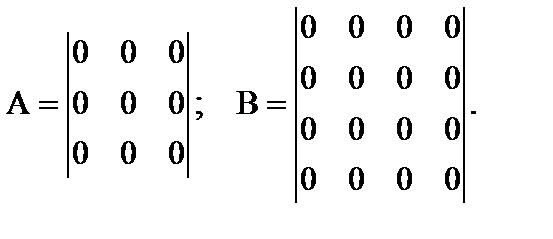
6. Единичная матрица – элементы главной диагонали матрицы равны единице, остальные элементы равны нулю.

7. Симметричная матрица – элементы матрицы сверху и снизу от главной диагонали имеют одинаковые значения (а₁₂ = а₂₁, а₁₃ = а₃₁ и т.д.).

8. Действительная матрица – все элементы матрицы представлены действительными числами.

9. Комплексная матрица – некоторые или все элементы матриц представляются комплексными числами.

10. Символьная матрица – в качестве элементов матрицы используются символьные переменные или выражения.

11. Блочная матрица – элементы матрицы представлены другими матрицами

Матрицы могут иметь различную структуру (портрет) – графическое изображение элементов матриц отличных от нуля:

1. Верхняя треугольная матрица

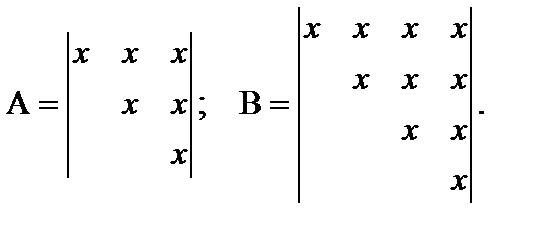
2. Нижняя треугольная матрица

3. Диагональная матрица

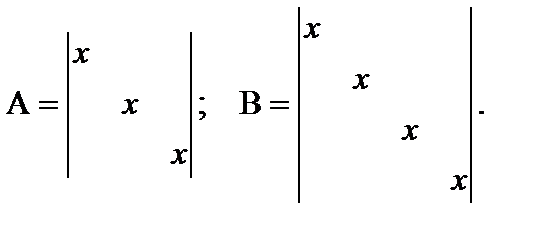
4. Ленточная матрица

5. Блочно-диагональная матрица

Различают также плотные и разреженные матрицы. Плотными можно считать такие матрицы, у которых большинство элементов ненулевые, в противном случае матрица считается разреженной (это понятие весьма условно):

а) плотная матрица б) разреженная матрица

ОСНОВНЫЕ ДЕЙСТВИЯ С МАТРИЦАМИ

1. Сложение (вычитание) матриц.Суммой (разностью) двух матриц А = (а_ij) и B = (b_ij), имеющих одинаковое количество строк и столбцов, называется матрица С = (с_ij), элементы которой равны суммам (разностям) соответствующих элементов матриц А и В (с_ij = а_ij ± b_ij).

2. Умножение матрицы на скалярную величину. Произведением матрицы А = (а_ij) на число α называется матрица, элементы которой получены из элементов матрицы А умножением на число α.

3. Умножение матриц А и В возможно только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом элементы матрицы произведения С = А×В определяются следующим образом: элемент с_ij i-той строки и j-того столбца матрицы С равен сумме произведений элементов i-той строки матрицы А на соответствующие элементы j-того столбца матрицы В.

При

А = (а_ij), i = 1, 2, ..., n; j = 1, 2, ..., m;

B = (b_ij), i = 1, 2, ..., р; j = 1, 2, ..., q;

получим

С = А×В = (с_ij), i = 1, 2, ..., n; j = 1, 2, ..., q, где

4. Транспонирование матрицы.При транспонировании матрицы строки становятся столбцами, а столбцы строками.

5. Обращение матрицы.Данная операция относится к квадратичным матрицам при условии, что определитель матрицы отличен от нуля (|А| ≠ 0).

Обратной матрицей по отношению к исходной называется матрица, которая, будучи умноженной как справа, так и слева на исходную матрицу дает единичную матрицу:

А×А^-1 = А^-1×А = 1.

Для обращения матриц небольшой размерности используют метод присоединения матрицы. Согласно этому методу обратная матрица вычисляется по выражению:

где |А| – определитель исходной матрицы, С^Т – транспонированная матрица алгебраических дополнений исходной матрицы:

МАТРИЧНЫЕ ПРЕОБРАЗОВАНИЯ

Матричные преобразования интерпретируются через действия над матрицами (чаще всего через умножение).

К элементарным матричным преобразованиям относятся:

1. Перестановка строк (столбцов) матрицы.

2. Умножение строки (столбца) на постоянную величину не равную нулю.

3. Многократное прибавление к какой-либо строке (какому-либо столбцу) другой строки (другого столбца).

Рассмотрим подробнее указанные выше матричные преобразования:

1.Перестановка произвольных двух строк матрицы выполняется левым умножением на перестановочную матрицу. Перестановочная матрица образуется из единичной матрицы путем перестановки элементов соответствующих строк следующим образом:

2.Перестановка произвольных двух столбцов матрицы выполняется правым умножением на перестановочную матрицу.

3.Умножение строки на постоянную величину отличную от нуля выполняется левым умножением на преобразователь. Преобразователь образуется из единичной матрицы путем замены элемента главной диагонали соответствующей строки на коэффициент следующим образом:

4.Умножение столбца на постоянную величину отличную от нуля выполняется правым умножением на преобразователь.

5.Многократное прибавление к какой-либо строке другой строки выполняется левым умножением на преобразователь. Преобразователь образуется из единичной матрицы путем замены нулевого элемента Е_i_,_j на коэффициент, где i – преобразуемая строка, j – строка преобразователь:

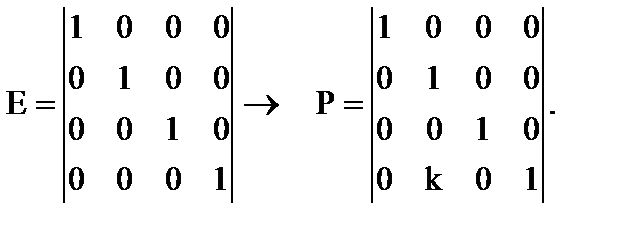
6.Многократное прибавление к какому-либо столбцу другого столбца выполняется правым умножением на преобразователь. Преобразователь образуется из единичной матрицы путем замены нулевого элемента Е_i_,_j на коэффициент, где i – столбец преобразователь, j – преобразуемый столбец:

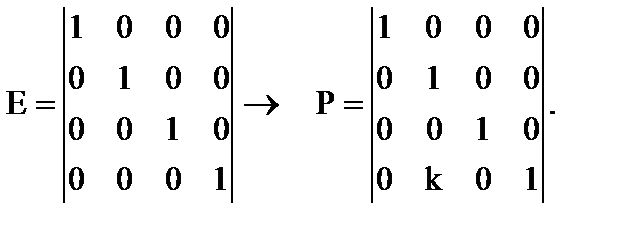
АЛГОРИТМ МЕТОДА ГАУССА

Решение системы n линейных алгебраических уравнений вида А∙х = bпо этому алгоритму состоит из двух этапов.

На первом этапе (прямой ход) исходная система за n однотипных шагов преобразуется таким образом, что матрица коэффициентов преобразованной системы становится верхней треугольной, т. е. все элементы, расположенные ниже ее главной диагонали, равны нулю.

На втором этапе (обратный ход) последовательно определяются значения неизвестных от х_n до x₁.

Последовательность операций, выполняемых при прямом ходе:

На первом шаге в исходной системе уравнений

a₁₁х₁ + а₁₂х₂ + … + а₁_nx_n = b₁

a₂₁х₁ + а₂₂х₂ + … + а₂_nx_n = b₂

……………………………..

a_n₁х₁ + а_n₂х₂ + … + а_nnx_n = b_n

первое уравнение делится на a₁₁. Далее х₁ исключается из всех последующих уравнений (i = 2, ..., n) путем умножения первого уравнения каждый раз на а_i₁ и вычитания из i-гo уравнения. В результате этих операций получается система уравнений с матрицей коэффициентов А⁽¹⁾:

х₁ + а₁₂⁽¹⁾х₂ + … + а₁_n⁽¹⁾x_n = b₁⁽¹⁾

0 + а₂₂⁽¹⁾х₂ + … + а₂_n⁽¹⁾x_n = b₂⁽¹⁾

……………………………..

0 + а_n₂⁽¹⁾х₂ + … + а_nn⁽¹⁾x_n = b_n⁽¹⁾

где

где i, j = 2, …, n.

Выполнение операций первого шага требует, чтобы элемент а₁₁, называемый ведущим, был отличен от нуля.

Второй шаг состоит в исключении x₂ из уравнений 3, ..., n, полученной на первом шаге системы путем выполнения аналогичных операций при использовании в качестве ведущего элемента а₂₂⁽¹⁾ В результате система приводится к виду А⁽²⁾∙х = b⁽²⁾.

Третий и последующий шаги выполняются аналогично.

На k-м шаге элементы матрицы A⁽^k⁾ и столбца b⁽^k⁾ определяются по выражениям:

i, j = k + 1, …, n.

При прямом ходе ведущими элементами последовательно выступают а₁₁, а₂₂⁽¹⁾, а₃₃⁽²⁾, …, а_nn⁽ⁿ^-1) и их отличие от нуля является условием осуществимости процесса вычислений.

В результате выполнения n шагов образуется система уравнений вида

х₁ + а₁₂⁽¹⁾х₂ +…+ а₁₍_n_-2)⁽¹⁾х_n_-2 + а₁₍_n_-1)⁽¹⁾х_n_-1 + а₁_n⁽¹⁾х_n = b₁⁽¹⁾

х₂ +…+ а₁₍_n_-2)⁽²⁾х_n_-2 + а₁₍_n_-1)⁽²⁾х_n_-1 + а₁_n⁽²⁾х_n = b₁⁽²⁾

………………………………………………………….

х_n_-2 + а₍_n_-2)(_n_-1)⁽ⁿ^-2)х_n_-1 + а₍_n_-2)_n⁽ⁿ^-2)х_n = b_n_-2⁽ⁿ^-2)

х_n_-1 + а₍_n_-1)_n⁽ⁿ^-1)х_n = b_n_-1⁽ⁿ^-1)

х_n = b_n⁽ⁿ⁾

На этапе обратного хода определяются искомые неизвестные от х_n до х₁.

Дата добавления: 2018-08-06; просмотров: 276; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!