ПРИМЕНЕНИЕ МЕТОДА НЬЮТОНА ПРИ РЕШЕНИИ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ ЗАДАЧ
Метод Ньютона является одним из наиболее эффективных методов решения самых разных нелинейных задач.
Пусть дана исходная система нелинейных уравнений:
(1)
Чтобы привести расчетную формулу метода Ньютона, через 
обозначим матрицу Якоби:
(2)
Итерационная формула метода Ньютона для вычисления корней нелинейной системы уравнений (1) имеет вид:
(3)
Формула (3) предполагает использование трудоемкой операции обращения матрицы, поэтому непосредственное ее использование для вычисления 
не всегда целесообразно. Преобразуем (3) следующим образом. Перенося 
влево и умножая результат на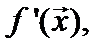 
получаем эквивалентную системе (2) систему линейных алгебраических уравнений
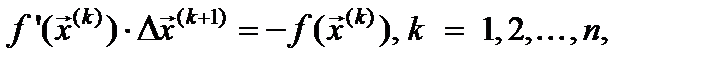(4)
относительно разности 
Решив систему линейных алгебраических уравнений (4) каким-либо приемлемым методом, вычисляем очередное приближение к корню
(5)
Если 
в достаточно малой окрестности корня системы (1), то в этой окрестности метод Ньютона сходится, причем с квадратичной скоростью, т.е. если 
то 
Квадратичная скорость сходимости метода Ньютона позволяет использовать простой практический критерий окончания итерационного процесса
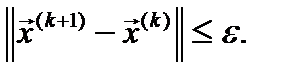(6)
|
|
|
Если начальное приближение выбрано удачно, то метод Ньютона сходится очень быстро.
ВЫРОЖДЕННОСТЬ МАТРИЦЫ, РАНГ И ДЕФЕКТ МАТРИЦЫ
Вырожденной называется квадратная матрица, определитель которой равен нулю.
Ранг матрицы – наивысший из порядков всевозможных ненулевых миноров этой матрицы.
Дефектом матрицы называется разность min (m, n) – r, где m – количество столбцов, n – количество строк, r – ранг матрицы. Если дефект матрицы равен нулю, то матрица имеет максимально возможный ранг.
Эквивалентные условия вырожденности:
· строки и столбцы матрицы линейно зависимы. Иными словами в вырожденной матрице существует как минимум две строки (или два столбца) хi и хj, отвечающие условию ахi = хj, где а – скаляр. В частности вырождена любая квадратная матрица, содержащая нулевой столбец или строку.
· Квадратная матрица А вырождена тогда и только тогда, когда существует ненулевой вектор х, такой что Ах = 0. Иными словами линейный оператор, соответствующий матрице в стандартном базисе, имеет ненулевое ядро. (линейный оператор – обобщение линейной числовой функции на случай более общего множества аргументов и значений; ядро – подмножество, которое отображается в нуль)
· Квадратная матрица вырождена тогда и только тогда, когда у нее есть хотя бы одно нулевое собственное значение.
|
|
|
Свойства:
· У вырожденной матрицы нет стандартной обратной матрицы.
· Ранг вырожденной матрицы меньше ее размера числа строк.
· Произведение вырожденной матрицы и любой квадратной матрицы дает вырожденную матрицу.
· Транспонирование вырожденной матрицы оставляет ее вырожденной.
· Умножение вырожденной матрицы на скаляр оставляет ее вырожденной.
· Треугольная (и, в частности, диагональная) матрица вырождена тогда и только тогда, когда хотя бы один из ее элементов на главной диагонали нулевой.
· Если матрица А вырождена, то система уравнений Ах = 0имеет ненулевые решения.
· Перестановка строк или столбцов вырожденной матрицы дает вырожденную матрицу.
· Вырожденная матрица, рассматриваемая как линейный оператор, отображает векторное пространство в его подпространство меньшей размерности.
Дата добавления: 2018-08-06; просмотров: 337; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!