Задачи на работу и производительность
Данный тип задач решается по аналогии с простыми текстовыми задачами на производительность: всю работу принято считать равной 1, искомую величину обозначают за х. При этом 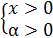 .
.
Задача 8:
Мастер и подмастерье вместе выполняют заказ за t часов. За какое время всю работу выполнит каждый, если мастер на выполнение работы тратит на 6 часов меньше, чем подмастерье? При условии, что tне превосходит 20 часов.
Решение:
Задача решается при помощи уравнения, роль параметра играет время совместной работы.
Примем за xч время работы мастера; так как он тратит на 6 часов меньше, то время работы подмастерья – х+6 часов. Учитываем, что х>0 и 0<t≤20.
Примем всю выполненную работу за 1, тогда  –общая скорость выполнения работы мастера и подмастерья. Эта величина равна сумме скоростей выполнения работ мастера и подмастерья:
–общая скорость выполнения работы мастера и подмастерья. Эта величина равна сумме скоростей выполнения работ мастера и подмастерья: 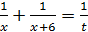 . Решим данное уравнение.
. Решим данное уравнение.
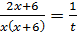 ;
;  ;
; 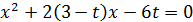
Данное уравнение может быть только квадратным, так как параметр t не входит в состав коэффициента а. Следовательно, нужно найти значение D и рассмотреть его значения.
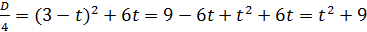 .
.
1) 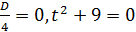 , то есть
, то есть  . Так как t –число положительное, корнем является только t=3.
. Так как t –число положительное, корнем является только t=3.
Подставляем найденное значение t в исходное уравнение: 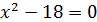 , то есть
, то есть 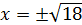 . Но значение х может быть только положительным, поэтому
. Но значение х может быть только положительным, поэтому  – время работы мастера, а время работы подмастерья –
– время работы мастера, а время работы подмастерья –  .
.
2) 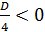 , то есть
, то есть 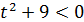 . Решение данного неравенства изображено на рисунке 12:
. Решение данного неравенства изображено на рисунке 12:
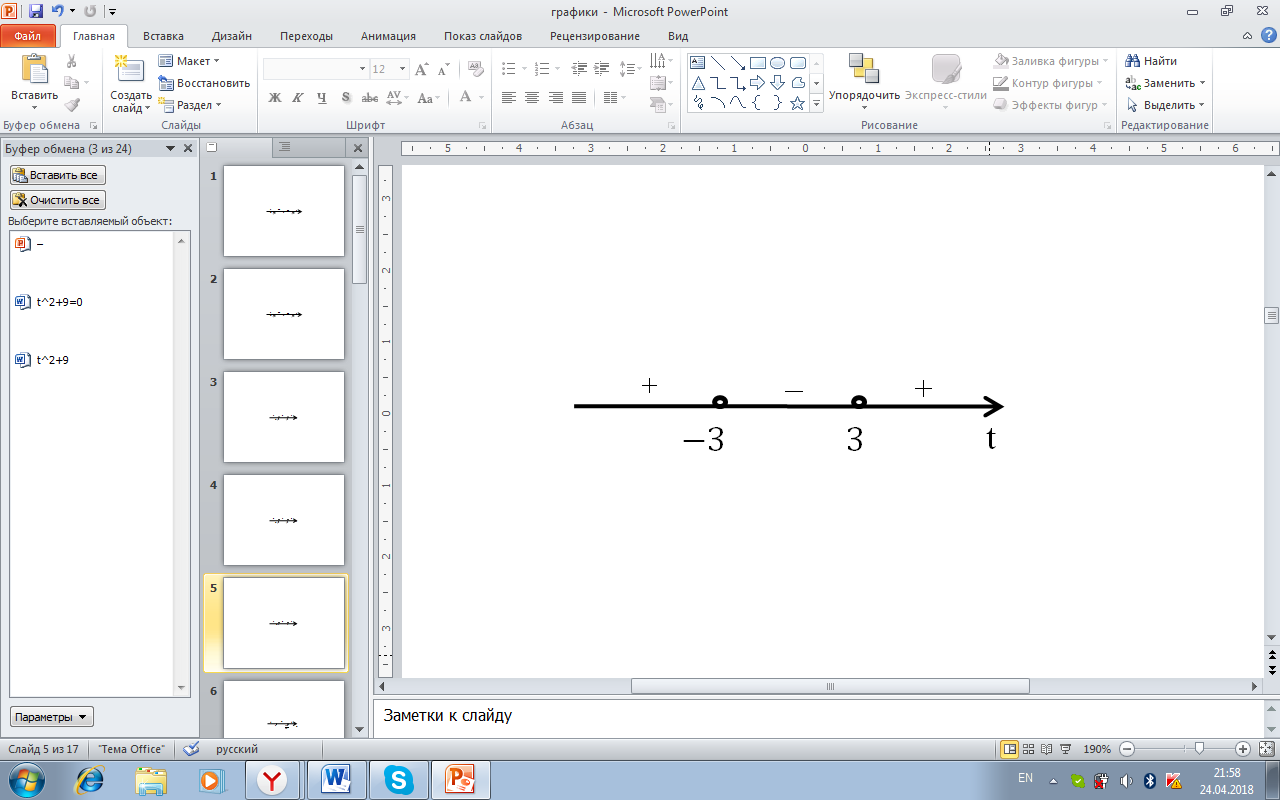
Рисунок 12. Решение неравенства 
Условиям удовлетворяет 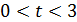 .
.
|
|
|
Когда дискриминант отрицательный, уравнение 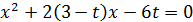 не имеет корней, а так как a>0, то ветви параболы направлены вверх иx всегда будет положительным: x>0 –время работы мастера, x>6 – время работы подмастерья.
не имеет корней, а так как a>0, то ветви параболы направлены вверх иx всегда будет положительным: x>0 –время работы мастера, x>6 – время работы подмастерья.
3) 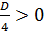 , то есть
, то есть 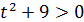 . Решение данного неравенства изображено на рисунке 13:
. Решение данного неравенства изображено на рисунке 13:

Рисунок 13. Решение неравенства 
Учитывая, что 0<t≤20, условию удовлетворяет интервал (3;20].
При положительном дискриминанте уравнение 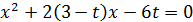 имеет два корня:
имеет два корня:
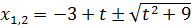 .
.
Рассмотрим каждый корень в отдельности, учитывая, что x>0:
I. 
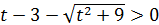 ;
; 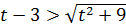 ;
; 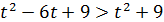 ;
;
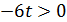 ;
;  . Следовательно,
. Следовательно,  – не корень.
– не корень.
II. 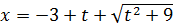
 ;
;  ;
; 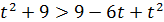 ;
; 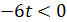 ;
; 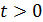 . Следовательно, время работы мастера
. Следовательно, время работы мастера 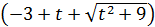 ч, а подмастерья: 6
ч, а подмастерья: 6 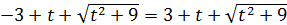 часов.
часов.
Ответ: 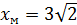 ,
, 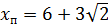 приt=3;
приt=3; 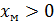 и
и  при
при 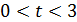 ;
;
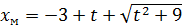 и
и  при 3<t≤20.
при 3<t≤20.
Задача 9:
За время t первый столяр сделал на 6 заготовок больше, чем второй. Потом второй столяр увеличил производительность на 0,4 детали и за целое число минут догнал и обогнал первого столяра на 4 детали. При каком наибольшем возможном времени t это возможно?
Решение:
Для решения данной задачи нужно ввести две переменных: x– начальная производительность первого столяра, а y – производительность второго. Сделано заготовок за время t: xt=yt+6. Позже второй увеличил производительность на 0,4 детали, то есть его производительность стала (y+0,4) деталей. Через целое число минут m второй столяр обогнал первого на 4 детали, то есть за время m он сделал на 6+4=10 деталей больше, чем первый. То есть (y+0,4)m=xm+10 деталей. Составим из полученных уравнений систему:
|
|
|
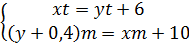 , учитывая, что
, учитывая, что 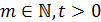 .
.
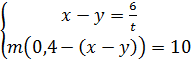 ;
;  ;
; 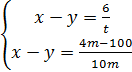 ;
;
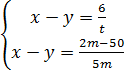 .
.
Очевидно, что при равенстве левых частей равны и правые части:
 ;
; 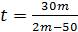 ;
; 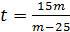 .
.
Рассмотрим выражение 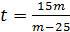 : так как t>0
: так как t>0 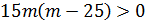 . Решением данного неравенства являются m=0 и m=25, значениями неравенства являются промежутки
. Решением данного неравенства являются m=0 и m=25, значениями неравенства являются промежутки 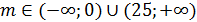 . Условиям задачи удовлетворяет только m>25.
. Условиям задачи удовлетворяет только m>25.
В задаче требуется найти наибольшее возможное t. Очевидно, что дробь 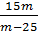 принимает наибольшее значение, когда знаменатель является наименьшим. Учитывая, что m>25 и
принимает наибольшее значение, когда знаменатель является наименьшим. Учитывая, что m>25 и 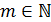 , m=26. Подставим данное число в выражение для t:
, m=26. Подставим данное число в выражение для t:
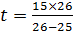 =390 (мин) – данное значение является ответом на вопрос задачи.
=390 (мин) – данное значение является ответом на вопрос задачи.
Ответ: 390 минут.
Задача 10:
В бассейн проведены три насоса. Первыйоткачивает 60 м3 в час, второй откачивает на 4v м3 в час меньше, чем первый (0<v<30), а третий – на 22vм3больше, чем первый. Работая вместе, первый и второй насос выкачивают  заполненного на весь объём бассейна, а потом все три насоса вместе выкачиваютоставшуюся воду из бассейна. При каком значении v бассейн опустеет быстрее всего?
заполненного на весь объём бассейна, а потом все три насоса вместе выкачиваютоставшуюся воду из бассейна. При каком значении v бассейн опустеет быстрее всего?
Решение:
Задача решается при помощи уравнения, роль параметра играет производительность труб.
|
|
|
Так как скорость первого насоса 60 м3, тогда скорость второго –(60–4v) м3, а третьего – (60+22v)м3. Одновременная работа первого и второго длилась время t1: 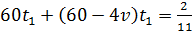 (1). А совместная работа трёх насосов длилась
(1). А совместная работа трёх насосов длилась  :
: 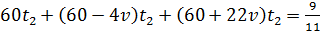 (2). Всё время работы равно
(2). Всё время работы равно 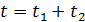 . Выразим из уравнений (1) и (2)
. Выразим из уравнений (1) и (2)  и
и  , чтобы найти t.
, чтобы найти t.
1) Рассмотрим уравнение 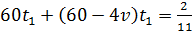 .
.
 ;
; 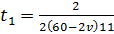 ;
; 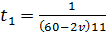 .
.
2) Рассмотрим уравнение 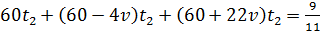 .
.
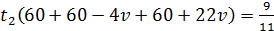 ;
;  ;
; 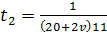 .
.
3) 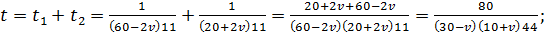
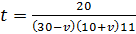 .
.
Бассейн опустеет быстрее, чем меньше пройдёт времени, то есть когда знаменатель дроби  будет наибольшим, учитывая, что 0<v<30.
будет наибольшим, учитывая, что 0<v<30.
Рассмотрим значения числителя при  .Так как во всех выражениях числителя будет присутствовать множитель 11, его можно не учитывать, а рассматривать наибольшее возможное
.Так как во всех выражениях числителя будет присутствовать множитель 11, его можно не учитывать, а рассматривать наибольшее возможное 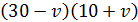 .
.
Пусть 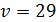 , тогда
, тогда 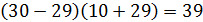 .
.
Пусть  , тогда
, тогда 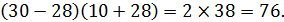
Повторяем данную процедуру, пока не получим число, которое будет меньше предыдущего.
Пусть 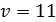 , тогда
, тогда  .
.
Пусть  , тогда
, тогда 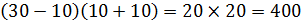 .
.
Пусть 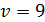 , тогда
, тогда 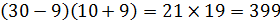 .
.
Очевидно, что числа дальше будут лишь уменьшаться, поэтому наибольшее значение выражение 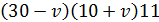 примет при v=10, тогда данное число и есть ответ на вопрос задачи.
примет при v=10, тогда данное число и есть ответ на вопрос задачи.
Ответ: 10 м3
Геометрические задачи
Такие задачи встречаются редко, поэтому решение производится по общему алгоритму: «вопрос задачи» обозначают за х, составляют уравнение с параметром на основе условия задачи, преобразуют его, рассматривают значения параметра и чему при этих значениях равен х. Не забывая, что длина – величина всегда положительная, поэтому х и параметр α будут больше 0.
|
|
|
Задача11:
Дан квадрат со стороной, длина которогоk м. От его вершин в направлении обхода по часовой стрелке проведены равные отрезки с концами в точках a, b, c и d, которые в свою очередь соединены прямыми. Площадь квадрата abcd равна S м2. Определите длину отрезка между вершиной первоначального квадрата и точкой a в направлении по часовой стрелке.
Решение:
Данная задача является задачей на поиск длины, она решается через уравнение, роль параметра играет длина стороны k.
Для решения данной задачи необходимо построить чертёж [рис. 14]:
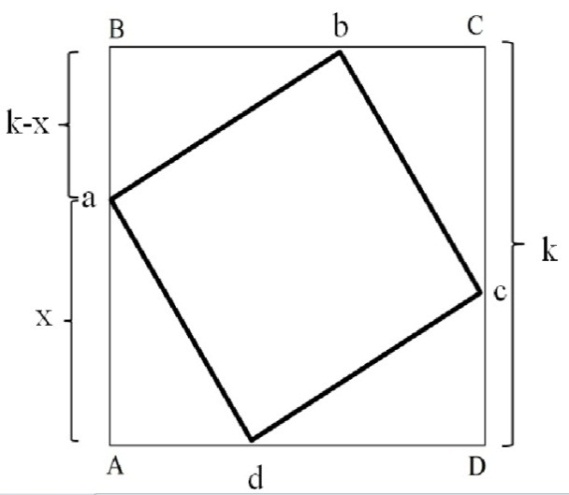
Рисунок 14. Квадраты ABCD и abcd
Примем длину отрезка Aa за х (х>0), тогда длины aB=bC=cD=dA=k-x. Сторона квадрата abcd в квадрате, по т. Пифагора, равна 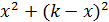 . При этом нам сказано, что площадь abcd равна S. Площадь квадрата равна квадрату его стороны, то есть
. При этом нам сказано, что площадь abcd равна S. Площадь квадрата равна квадрату его стороны, то есть 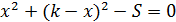 . Преобразуем полученное уравнение:
. Преобразуем полученное уравнение:
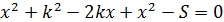 ;
; 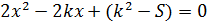
Найдём значение дискриминанта данного уравнения, воспользовавшись формулой  :
:
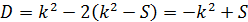
Рассмотрим значение дискриминанта. Возможны три случая.
1) Если D<0, то 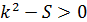 , то есть
, то есть 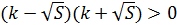 . Корнями данного неравенства являются числа
. Корнями данного неравенства являются числа 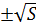 . Нанесём их на координатную прямую, изображённую на рисунке 15:
. Нанесём их на координатную прямую, изображённую на рисунке 15:
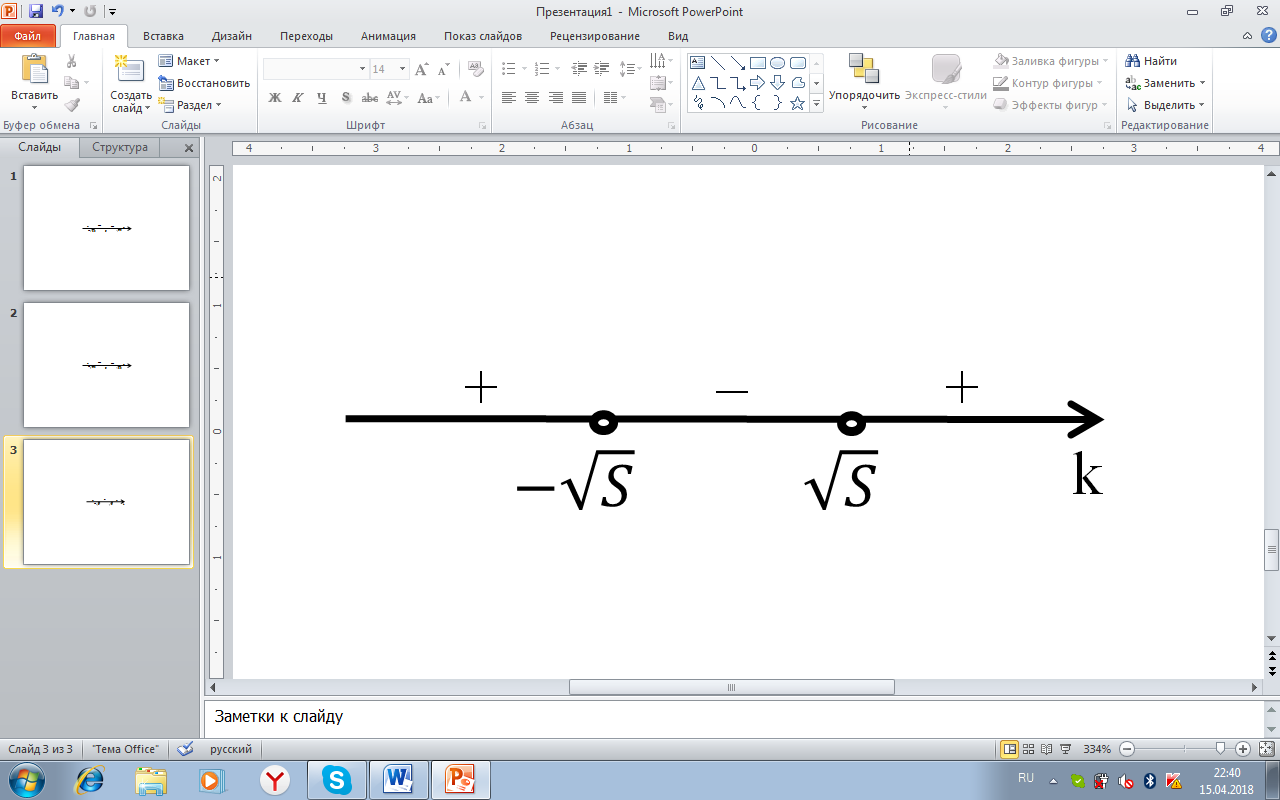
Рисунок15. Решение неравенства (k-√S)(k+√S)>0 при D<0
Условию удовлетворяют интервалы  ) и (
) и ( 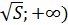 .Так как k – величина положительная, возьмём только второй интервал, то есть k>
.Так как k – величина положительная, возьмём только второй интервал, то есть k> 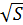 .
.
Учитывая, что при D<0 корней у уравнения 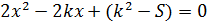 нет, а ветви параболы направлены вверх, то при данном значении k решением может являться любое положительное число х.
нет, а ветви параболы направлены вверх, то при данном значении k решением может являться любое положительное число х.
2) Если D=0, то есть 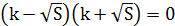 → k=
→ k= 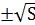 , то уравнение
, то уравнение 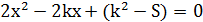 будет иметь один корень. Причём k=
будет иметь один корень. Причём k= 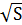 >0.Найдём х:
>0.Найдём х:
 →
→ 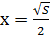 .
.
3) Если D>0, тогда уравнение 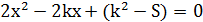 имеет решения при
имеет решения при 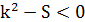 , они изображены на рисунке 16.
, они изображены на рисунке 16.
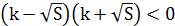 → k=
→ k= 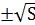
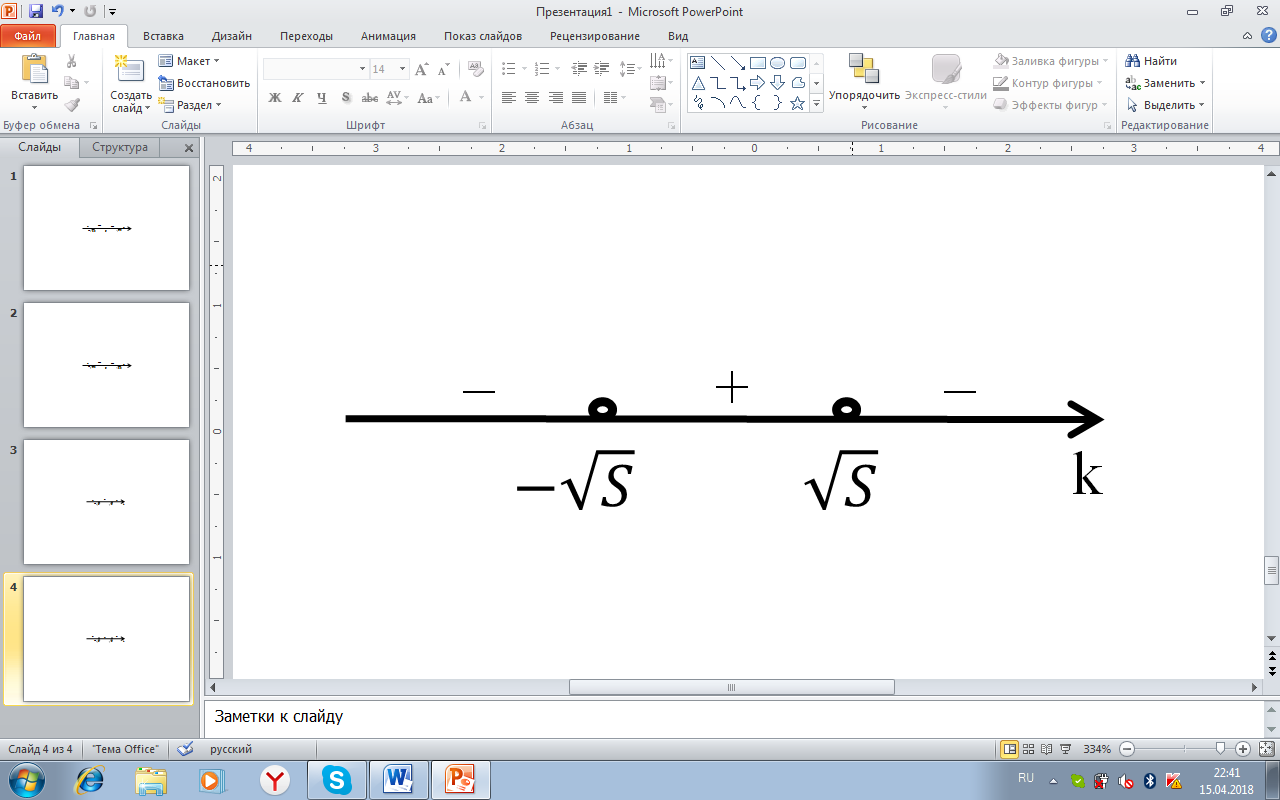
Рисунок16. Решение уравнения 2x2-2kx+(k2-S)=0 при D>0
Условию k>0 удовлетворяет интервал 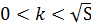 .
.
Тогда  ,
,
Ответ:х – любое положительное число, если k> 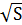 ;
; 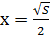 , если k=
, если k= 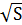 ;
;
 , если
, если 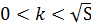 .
.
Задача 12:
Дан конус. Его осевое сечение является правильным треугольником с площадью S. Какие значения может принимать радиус основания конуса, если площадь его осевого сечения менее 9 см2?
Решение:
В роли параметра в этой задаче выступает площадь сечения S.
Для начала решения рассмотрим чертёж [рис.17]:

Рисунок 17. Осевое сечение конуса  ABS'
ABS'
Радиусом конуса является отрезок ОВ; так как треугольник правильный, то радиус основания конуса равен половине стороны треугольника а. Формула площади равностороннего треугольника вычисляется по формуле 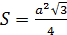 , где a=2r, то есть
, где a=2r, то есть 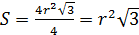 .
.
Из условия задачи ясно, что 0<S<9, поэтому мы можем составить следующее двойное неравенство: 0< 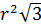 <9. Учитывая, что
<9. Учитывая, что 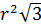 всегда больше нуля, можем решить неравенство
всегда больше нуля, можем решить неравенство 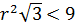 и взять только ту часть, где r>0.
и взять только ту часть, где r>0.
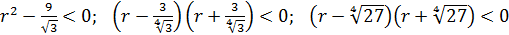 .
.
Решением данного неравенства служит интервал 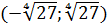 , а учитывая, что r– длина, величина всегда положительная, то
, а учитывая, что r– длина, величина всегда положительная, то  .
.
Ответ:  при 0<S<9.
при 0<S<9.
Экономические задачи
Задача 13:
Коллекционер купил юбилейные монеты достоинством 10 рублей на 4500 руб., а памятных монет на 5000 руб. Цена одной памятной монеты на 200α больше, чем цена монеты в 10 рублей, где 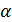 – натуральное число. При этом юбилейных монет куплено на 5 штук больше, чем памятных. Сколько монет каждого вида купил коллекционер?
– натуральное число. При этом юбилейных монет куплено на 5 штук больше, чем памятных. Сколько монет каждого вида купил коллекционер?
Решение:
Данная задача решается при помощи уравнения, роль параметра играет цена предмета.
Обозначим за х – количество памятных монет, тогда количество юбилейных монет равно (х+5). Так как дана сумма, потраченная на каждый вид монет, то цена одной монеты каждого вида будет выражаться через формулу 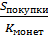 :
: 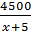 и
и 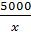 . По условию, цена памятной монеты на 200α больше, тогда уравнение будет иметь следующий вид:
. По условию, цена памятной монеты на 200α больше, тогда уравнение будет иметь следующий вид: 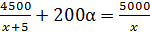 . Теперь можно приступить к решению, учитывая, что
. Теперь можно приступить к решению, учитывая, что 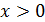 и
и 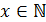 ,
, 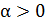 .
.
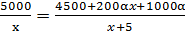 ;
; 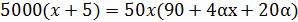 ;
;
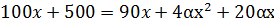 ;
; 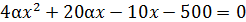 ;
;
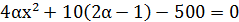 ;
; 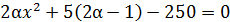 .
.
Так как, по условию, α>0, уравнение при любом α является квадратным. Следовательно, нужно найти дискриминант полученного уравнения, чтобы рассмотреть возможные значения параметраα:
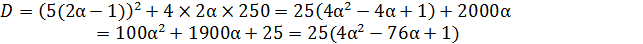
Далее нужно рассмотреть случаи, когда дискриминант принимает положительные значения, отрицательные или равен 0.
1) D<0, 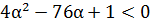 [рис.18].
[рис.18].


Рисунок 18. Решение неравенства 4α2-76α+1<0
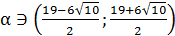 .
.
При значении отрицательном значении D уравнение 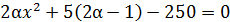 не имеет корней.
не имеет корней.
2) D=0, 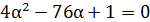 , следовательно, α=
, следовательно, α=  . Корни нанесены на координатную прямую [рис.19].
. Корни нанесены на координатную прямую [рис.19].
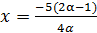 ;
;
Так как 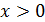 и
и 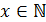 , то
, то 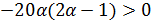 ;
; 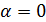 и
и 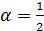
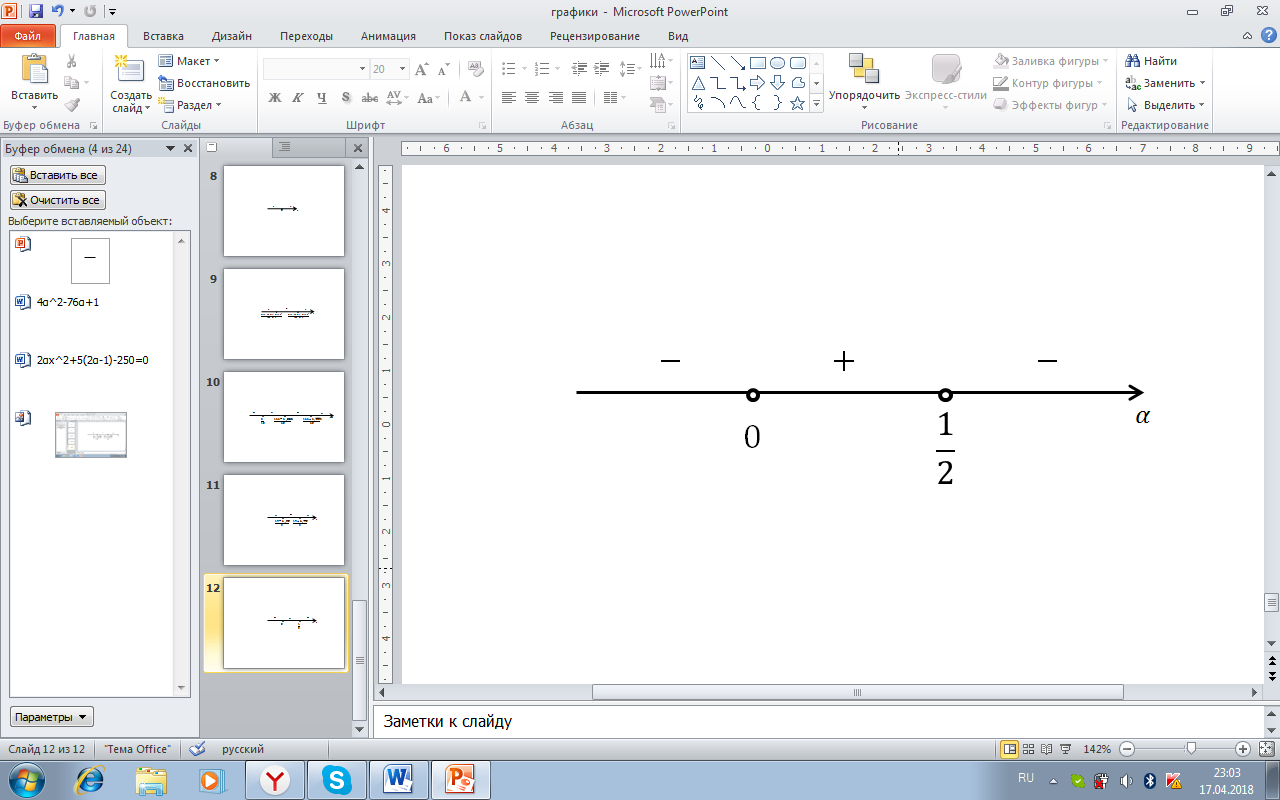
Рисунок 19. Значения уравнения 4α2-76α+1=0
Следовательно,  ,
,  .
.
3) D>0, 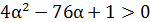 [рис.20]
[рис.20]

Рисунок 20. Значения неравенства 4α2-76α+1>0
Условиям удовлетворяют промежутки  .
.
Когда D положителен, уравнение 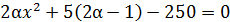 имеет следующие корни:
имеет следующие корни:

Теперь нужно проверить выполнение условия 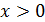 :
:
1. 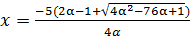 [рис.21]
[рис.21]
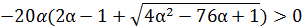

1) α=0
2) 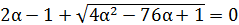
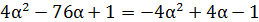
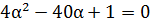
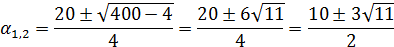
Для проверки знаков на каждом промежутке берём только те α, которые входят в промежутки  .
.
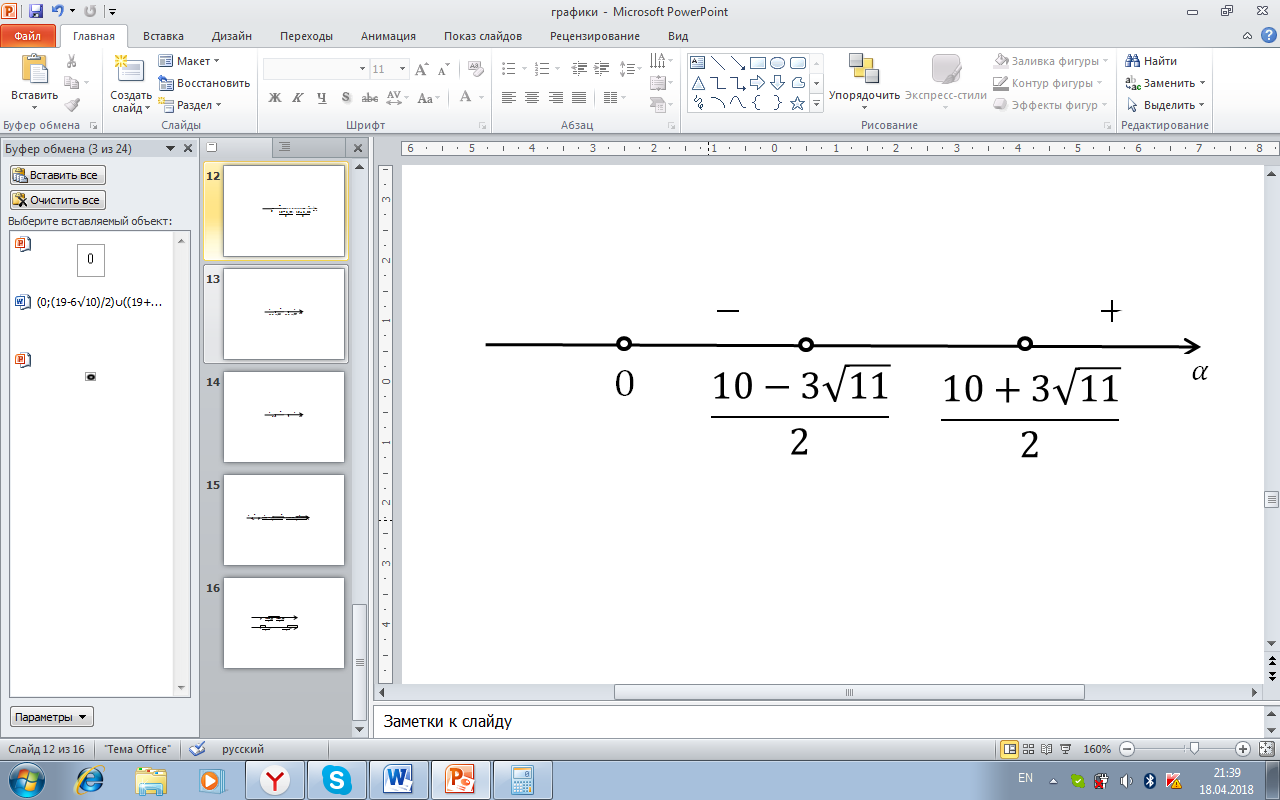
Рисунок 21. Проверка условия x=(-5(2α-1+√(4α2-76α+1)))/4α
Условиям удовлетворяет интервал 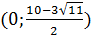 ; для α из интервала
; для α из интервала 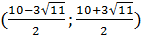 подкоренное выражение равно 0, чего быть не может; интервал
подкоренное выражение равно 0, чего быть не может; интервал 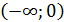 не рассматривается, так как α>0.
не рассматривается, так как α>0.
Для нахождения значений α нужно решить систему 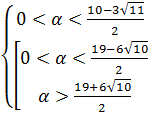
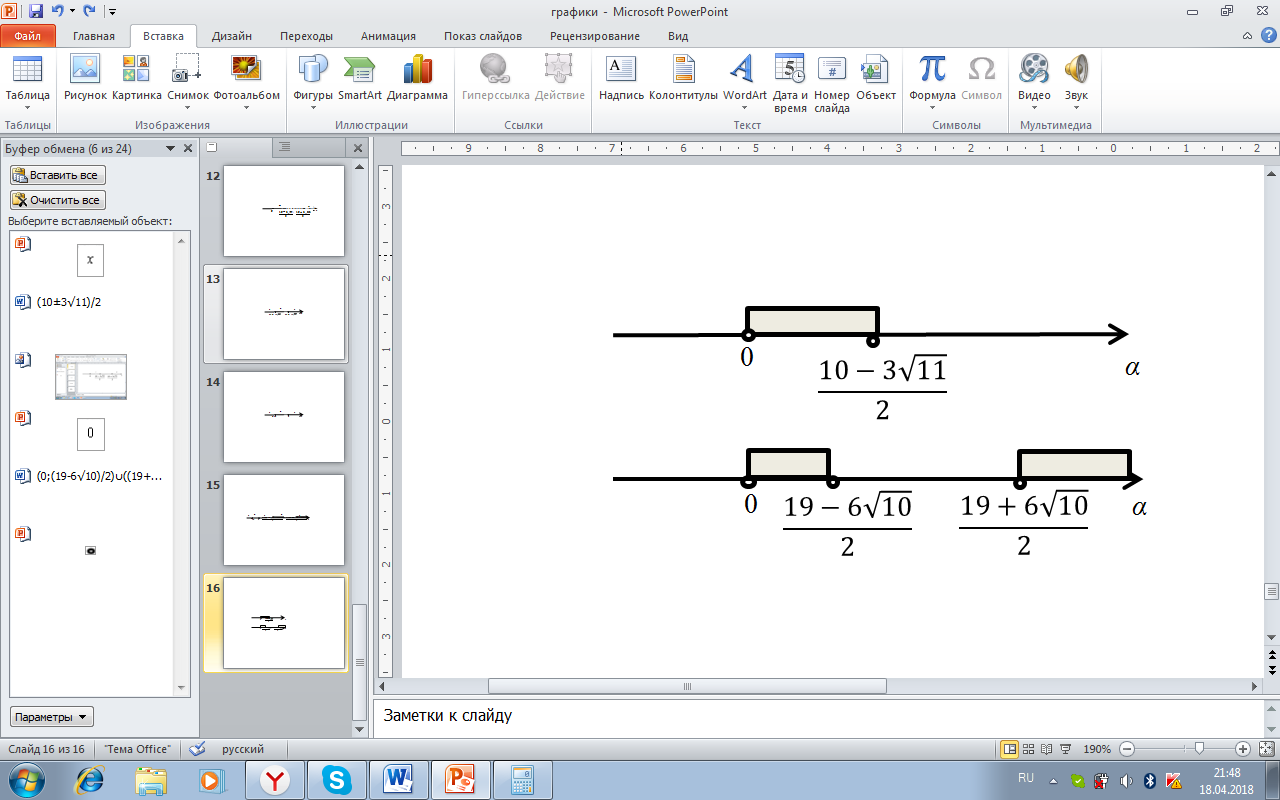
Рисунок 22. Решение системы неравенств для параметра α
Итоговое значение параметра α: 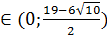 .
.
2.  [рис.23]
[рис.23]
 ;
;
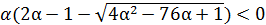 ;
;
1) α=0
2) 
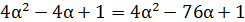 ; α=0
; α=0
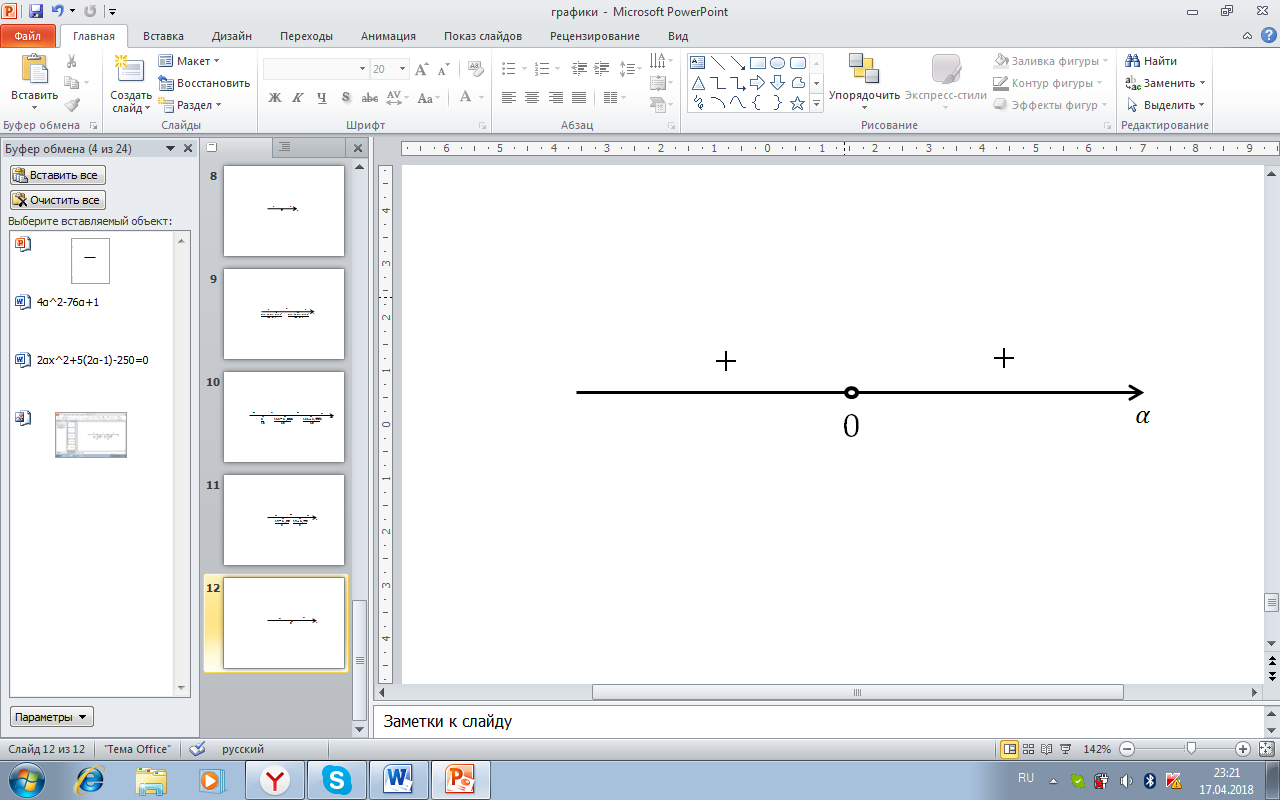
Рисунок 23. Проверка значений x=(-5(2α-1-√(4α^2-76α+1)))/4α
Данное неравенство не имеет корней. Поэтому рассматриваем только 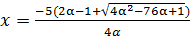 . Но, по условию, х – количество памятных монет; тогда юбилейных монет куплено
. Но, по условию, х – количество памятных монет; тогда юбилейных монет куплено 
Ответ:  ,
, 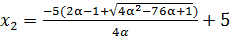 , если
, если 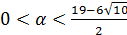 .
.
Задача 14:
Коллекционер купил редкие почтовые марки на 3000 руб., а памятных монет на 7000 руб. Цена одной памятной монеты на 5α больше, чем цена монеты. При этом всего предметов куплено не более 40. Какова цена монеты, марки?
Решение:
Так как в задаче есть выражение «не более», то математической моделью будет неравенство; роль параметра играет цена предмета.
Обозначим за хруб. цену марки, тогда цена памятной монеты равна (x+5α). Так как дана сумма, потраченная на каждый вид монет, то количество монет каждого вида будет выражаться через формулу 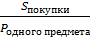 :
:  и
и 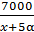 . По условию, купленных предметов не больше 40, тогда неравенство будет иметь следующий вид:
. По условию, купленных предметов не больше 40, тогда неравенство будет иметь следующий вид: 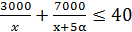 . Теперь можно приступить к решению, учитывая, что
. Теперь можно приступить к решению, учитывая, что 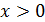 и
и 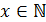 ,
, 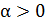 .
.
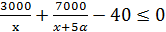 ;
; 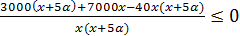 ;
;
 ;
;
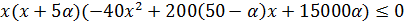 ;
;
 ;
;
Произведение равно нулю, когда хотя бы один из множителей равен нулю, поэтому для решения методом интервалов нужно найти корни каждого множителя.
Очевидно, чтоэтоx=0, 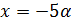 и корни уравнения
и корни уравнения 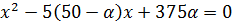 . Рассмотрим дискриминант последнего уравнения, чтобы определить множество значений
. Рассмотрим дискриминант последнего уравнения, чтобы определить множество значений 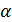 , учитывая, что, по условию задачи,
, учитывая, что, по условию задачи, 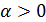 .
.

Далее нужно рассмотреть случаи, когда дискриминант принимает положительные значения, отрицательные или равен 0.
1) D<0, 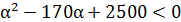 [рис.24].
[рис.24].
 .
.
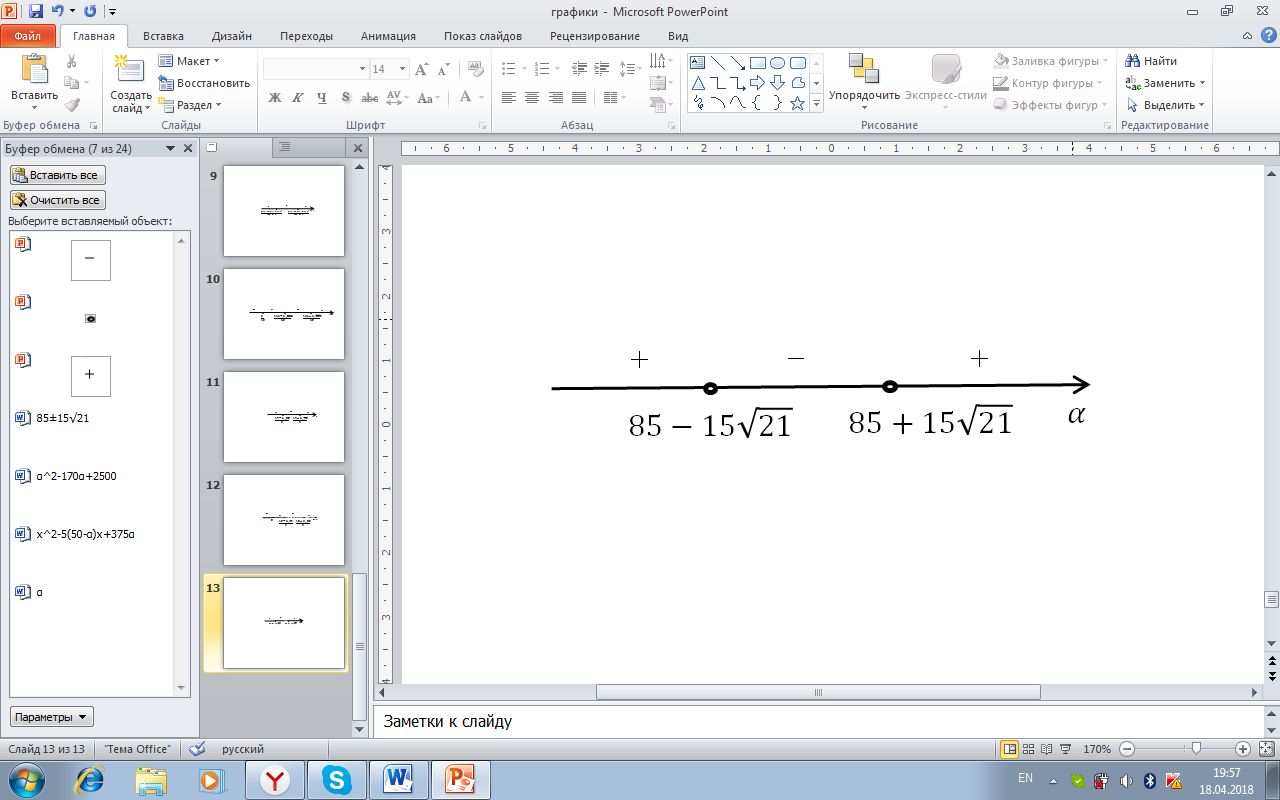
Рисунок 24. Решение неравенства α2-170α+2500<0
Условию удовлетворяет  .
.
При значении отрицательном значении D уравнение 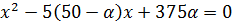 не имеет корней. Следовательно, корнями неравенства
не имеет корней. Следовательно, корнями неравенства  являются толькоx=0,
являются толькоx=0, 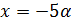 [рис.25].
[рис.25].

Рисунок 25. Корни неравенства x(x+5α)(x2-5(50-α)x+375α)≥0 при D<0
Получается, что 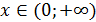 , так как x>0.
, так как x>0.
2) D=0, 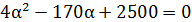 , следовательно, α=
, следовательно, α= 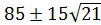 .
.
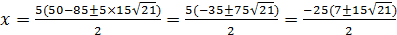 ;так же x=0 и x=−5(
;так же x=0 и x=−5(  )=−25(17
)=−25(17  . Все решения изображены на рисунке 26.
. Все решения изображены на рисунке 26.

Рисунок 26. Корни неравенства x(x+5α)(x2-5(50-α)x+375α)≥0 при D=0
Так как х>0, то условиям удовлетворяют интервалы 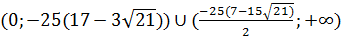 . При этом
. При этом 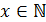 .
.
3) D>0, 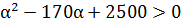 [рис.27]
[рис.27]

Рисунок 27. Решения неравенства α2-170α+2500>0
Условиям удовлетворяет  .
.
Тогда корни уравнения 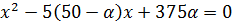 :
:
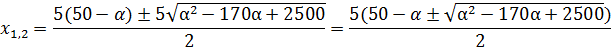
Получается, что корнями неравенства  являются
являются  , x=0 и х=
, x=0 и х= 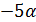 [рис.28].
[рис.28].

Рисунок 28. Решения неравенства x(x+5α)(x2-5(50-α)x+375α)≥0 при D>0
Условиям удовлетворяет два интервала: 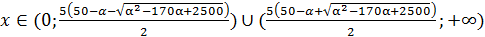 и
и 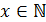 .
.
Ответ:  ;
;
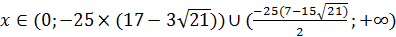 ,
, 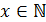 при α=
при α= 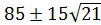 ;
;
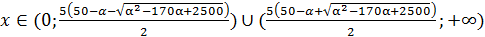 ,
, 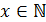 при
при  .
.
Задача 15:
Отправляясь в путешествие, турист рассчитывал истратить в дороге 720000 руб. В течение первых k дней его расходы совпадали с расчётными, а затем он стал расходовать в день в среднем на 10000 руб. больше, чем предполагал, и, задержавшись в пути на 1 день, вернулся домой, истратив на всё путешествие на 230000 руб. больше, чем предполагал первоначально. Сколько дней продолжалось путешествие? [1, стр.363]
Решение:
Эта задача решается при помощи уравнения, роль параметра играет количество дней пути k.
Примем за x дней – время всего путешествия. Так как путешествие длилось на 1 день дольше, то оно должно было длиться (x-1) дней. А значит, предполагаемые расходы туриста в день были равны 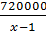 руб. Расходы совпадали с предполагаемыми только первые k дней, поэтому потраченная сумма за эти дни:
руб. Расходы совпадали с предполагаемыми только первые k дней, поэтому потраченная сумма за эти дни: 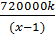 руб. Оставшиеся дни путешествия, то есть (x-k) дней, его расходы превышали планируемые на 10000 руб., то есть они составляли
руб. Оставшиеся дни путешествия, то есть (x-k) дней, его расходы превышали планируемые на 10000 руб., то есть они составляли  . За всё путешествие он истратил 950000 руб., то есть:
. За всё путешествие он истратил 950000 руб., то есть: 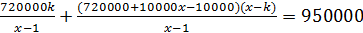 руб.
руб.
Решая данное уравнение, будем учитывать, что xи k–число дней, следовательно 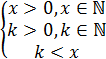 .
.
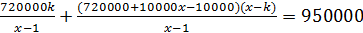 ;
; 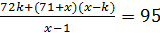 ;
;
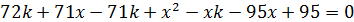 ;
;
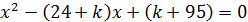 .
.
Данное уравнение может быть только квадратным, поэтому находим D.

Теперь рассмотрим корни 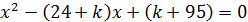 при различных значениях D.
при различных значениях D.
1) D=0, 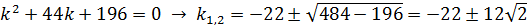
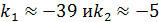 .
.
Данные значения не удовлетворяют условиям задачи, поэтому при D=0 уравнение 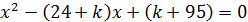 не имеет корней.
не имеет корней.
2) D<0, 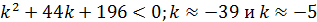 .
.
Нанесём полученные корни на координатную прямую [рис.29]:
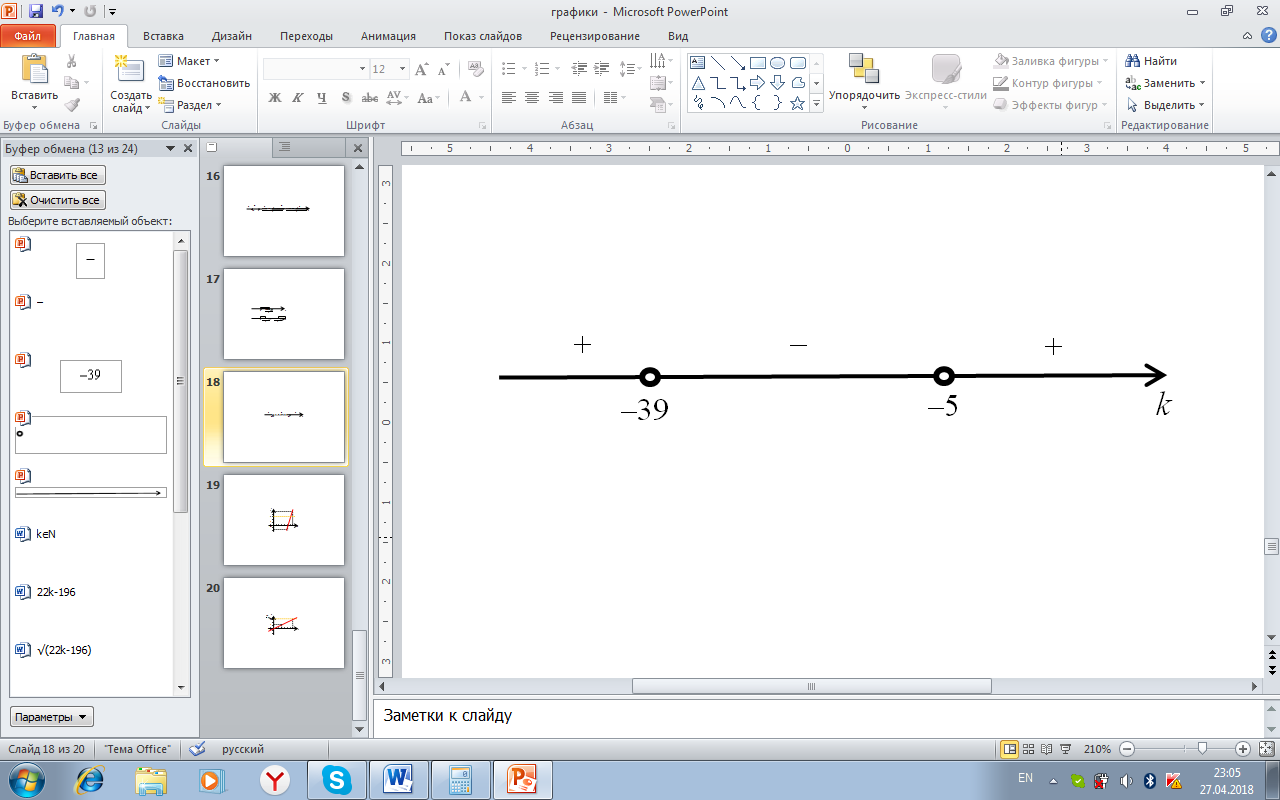
Рисунок 29. Решение неравенства 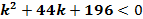
Решением неравенства является интервал (-39;-5), но данные значения не удовлетворяют условиям, следовательно, при D<0 уравнение 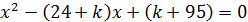 не имеет решений.
не имеет решений.
3) D>0, 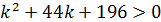 . Решение данного неравенства изображено на рисунке 30:
. Решение данного неравенства изображено на рисунке 30:

Рисунок 30. Решение неравенства 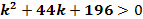
Условиям для kудовлетворяет только интервал 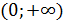 . Но при этом k<x.
. Но при этом k<x.
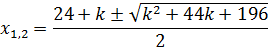
I. 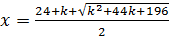
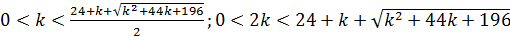 ;
;
Решаем неравенство  :
:

 ;
;
При  .
.
II. 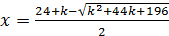
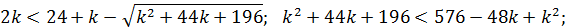
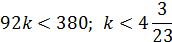
При 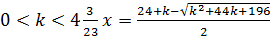 .
.
Ответ: 
 .
.
В данном разделе были рассмотрены параметрические текстовые задачи и на составление уравнений, и на составление неравенств, и задачи из каждой группы по содержанию. Во всех задачах был получен ответ, то есть значение переменной и значения параметра, при которых переменная принимает такое значение. Следовательно, любая задача может быть решена аналитическим методом.
Дата добавления: 2018-06-27; просмотров: 1517; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
