Различные виды текстовых задач с параметром и их решение

Классификация текстовых задач с параметром

Изучая литературу по данной теме, можно увидеть, что текстовые задачи, содержащие параметр, действительно являются задачами повышенного уровня сложности по сравнению с простыми текстовыми задачами. Потому что задачи с параметром – это задачи на сплавы, растворы, движение и работу. Конечно, встречаются другого вида текстовые задачи с параметром, но в упрощённом виде, без параметра, они тоже довольно часто встречаются в учебниках и пособиях.

Если рассматривать текстовые задачи, содержащие параметр, то можно разделить всё многообразие задач на две большие группы. Первая группа включает в себя задачи на составление уравнений, вторая – на составление неравенств. Задачи на составление неравенств легко отличить по наличию в них таких выражений, как «более» и «не более», «менее» и «не менее», «не позже» и «не раньше». Также от того, составлено уравнение или неравенство, зависит способ решения. Если в уравнениях рационально использовать приём умножения крест-накрест (свойство пропорции), то в неравенствах этого делать категорически нельзя. В случае неравенств решение осложняется тем, что необходимо переносить слагаемые из одной части в другую и приводить к общему знаменателю.

Итак, приведём классификацию текстовых параметрических задач.

I. По составленной математической модели:

1) задачи на составление уравнений;

2) задачи на составление неравенств.

II. По содержанию (условию) задачи:

1) задачи на растворы;

2) задачи на сплавы;

3) задачи на движение:

a) на суше;

b) на воде.

4) задачи на работу и производительность:

a) самостоятельная и совместная работа;

b) задачи о трубах или насосах.

5) геометрические задачи;

6) экономические задачи.

III. По роли параметра:

1) концентрация:

a) в задачах на растворы;

b) в задачах на сплавы;

2) объём:

a) в задачах на растворы;

b) в задачах на сплавы;

c) в задачах на работу (заполнение или осушение бассейна);

d) в геометрических задачах;

3) масса:

a) в задачах на растворы;

b) в задачах на концентрацию;

4) время:

a) в задачах на движение;

b) в задачах на работу и производительность;

5) скорость:

a) в задачах на движение;

b) в задачах на работу и производительность;

6) путь (в задачах на движение);

7) длина (в геометрических задачах);

8) цена (в экономических задачах);

9) количество (в экономических задачах).

Решение текстовых задач с параметром аналитическим методом

Решение текстовых задач, содержащих параметр, часто выполняется аналитическим методом.

Составление уравнений (или неравенств) в параметрических задачах строится по простому алгоритму:

1) обозначить одну величину (чаще всего это искомая величина) за х;

2) составить математическую модель, то есть составить уравнение (неравенство, систему уравнений или неравенств) на основе условия задачи;

3)проверитьобласть значений параметра.

Если после преобразований будут получены квадратные уравнения и неравенства, то для проверки области определения параметра, нужно сначала рассмотреть коэффициент а перед х², если в его состав входит параметр. При а=0 уравнение или неравенство будет линейным. Решить линейное уравнение или неравенство. Далее нужно рассмотреть случай, когда а≠0, то есть уравнение или неравенство является квадратным. При таком условии для решения необходимо найти дискриминант и рассмотреть три возможных случая: D<0, D=0, D>0. При этом выбирать только те промежутки, где значения параметра неотрицательно.После при данных значениях дискриминанта найти х.

Часто ограничения и параметра, и значения х в задаче прямо не указаны, но следуют из условия (например, концентрация раствора данного вещества не может быть меньше 0% и больше 100%).

4) решить составленное выражение;

5) записать ответ. Причём в нём нужно отразить, при каких значениях параметра αсуществует хи чему он равен.

Проиллюстрируемрешение каждого типа задач.

Задачи на растворы

Как правило, в них требуется узнать, сколько раствора нужно перелить из одного сосуда в другой для получения нужной концентрации вещества в растворе. Метод решения таких задач достаточно прост: искомый объём обозначается за х (переменную), параметром же обычно служит концентрация либо одного из исходных растворов, либо полученного. Далее составляется уравнение (или неравенство, в зависимости от формулировки задачи) на основе формулы: 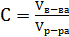, где C – концентрация 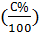, объём чистого вещества – V_в-ва=V_в-ва(1)+V_{в-ва(пер.)}, объём всего раствора –V_р-ра=V_р-ра(1)+ V_{р-ра(пер.)}.

Если составить уравнение таким образом и решить его, то в итоге будет получено значение х, выраженное через параметр α. Теперь необходимо проверить множество значений, которое может принимать параметр. Если в задаче дан объём сосудов, в которых находится раствор, тогда значение х должно лежать в диапазоне свободного объёма сосуда, куда переливают раствор. Если же объёма сосудов не дано, но х выражено в виде дроби, где α входит в знаменатель, то нужно найти такие значения, при которых дробь существует (знаменатель не равен 0).

Рассмотрим данный алгоритмна примере решения задач на составление и уравнения, и неравенства.

Задача 1:

В двух сосудах ёмкостью по 10 л содержится раствор серной кислоты. В первом из этих сосудов – 6 л раствора с объёмной долей вещества α, во втором – 8 л раствора, с объёмной долей 2α. Сколько раствора нужно перелить из второго сосуда в первый, чтобы объёмная доля в нём стала 0,2?

Решение:

Так как нет слов-сигналов (более, менее и других) данная задача решается при помощи составления уравнения.

Обозначим объём вещества, которое нужно перелить из II сосуда за х. В данной задаче параметр играет роль концентрации первоначальных растворов. Найдём объём вещества в первом сосуде: 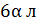. Объём вещества в перелитом растворе – 2αх. Объёмная доля вещества в новом растворе в I сосуде 0,2. Имеем уравнение 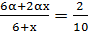. Решим данное уравнение:

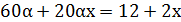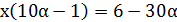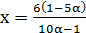; ; , где .

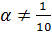Так как в I сосуд можно было долить до заполнения 4 л серной кислоты, запишем неравенство: 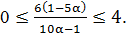Решим это неравенство:

;

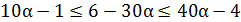Решение данного двойного неравенства равносильно решению системы неравенств: ; ; ;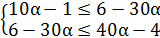

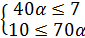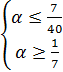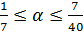
Ответ: 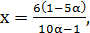при .

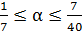Задача 2:

В один из сосудов ёмкостью по 8 л налито 5 л 60% раствора щёлочи, а во второй – 4 л 80% раствора щёлочи. Сколько раствора нужно перелить из второго сосуда в первый, чтобы в нём получился раствор с концентрацией щёлочи α?

Решение:

Данная задача решается через уравнение, параметром в ней выступает концентрация полученного раствора.

Примем перелитый объём раствора за х л. Из условия ясно, перелитый объём раствора не превышает 3 л, то есть .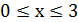

Найдём объём чистого вещества в первом растворе: 3 л (5*0,6=3). Тогда объём чистого вещества в перелитом растворе – 0,8*х л. Всего объём раствора в первом сосуде равен 5+х л. Составим уравнение: .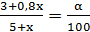

Решим полученное уравнение:

; ;

, .

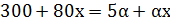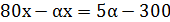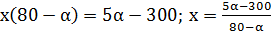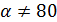Теперь подставляем х в составленное ранее неравенство: ;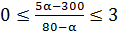

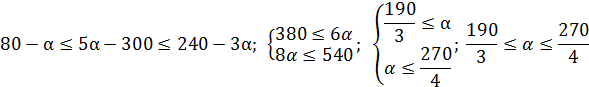
Ответ: 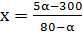при .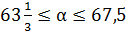

Задача3:

В лаборатории в два сосуда, вместимость каждого составляет 8 л, налит раствор щёлочи. В первый сосуд налито 5 л раствора с объёмной долей вещества 2α, во второй – 7 л раствора щёлочи с объёмной долей вещества α. Из второго сосуда в первый переливают некоторое количество щёлочи таким образом, что концентрация раствора в нём стала не менее 80%. Какое количество раствора нужно перелить?

Решение:

Данная задача решается при помощи неравенства, роль параметра в ней играют первоначальные концентрации растворов.

Приняв за х перелитое количество раствора, определим объёмную долю вещества в новом растворе: 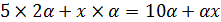. Объём нового раствора равен сумме объёмов смешанных растворов: 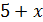. Подставим значения в формулу 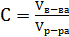и отметив, что полученная величина не меньше 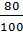, получим следующее неравенство: .

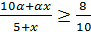До того как решать неравенство, следует рассмотреть ограничения, которые накладываются на значение переменной и параметра α. Так как вместимость сосуда равна 8 л и в нём уже налито 5 л первого раствора, то перелитый объём раствора может принимать следующие значения: 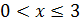. Большая объёмная доля вещества в первом растворе, поэтому рассматриваем возможные значения для 2α; объёмная доля вещества не может превышать 100%, следовательно, 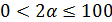, то есть 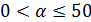.Теперь можно приступить к решению.

Для решения неравенств использованный в предыдущих примерах приём умножения крест-накрест не применим, поэтому необходимо перенести все слагаемые в левую часть и привести к общему знаменателю. Далее воспользоваться свойством неравенства: знак дроби совпадает со знаком произведения при всех значениях x, при которых дробь имеет смысл ( .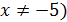

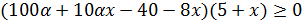
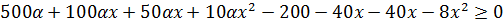
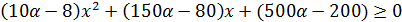
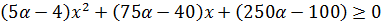– обозначим полученное неравенство (_*).

I. Допустим, что 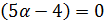, то есть 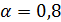, тогда неравенство 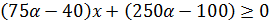будет линейным.

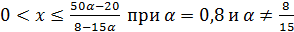Тогда , .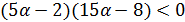

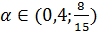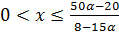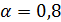Конечным ответом является при и .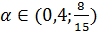

II. Теперь нужно найти дискриминант уравнения , когда .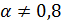

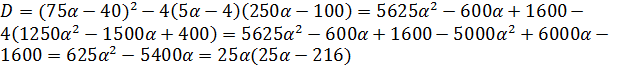Следующим этапом нужно рассмотреть три возможных значения D и соответствующие им значения х.

1) D<0, следовательно, . Корнями данного неравенства являются 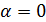и 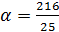. Нанесём их на координатную прямую[рис.1]

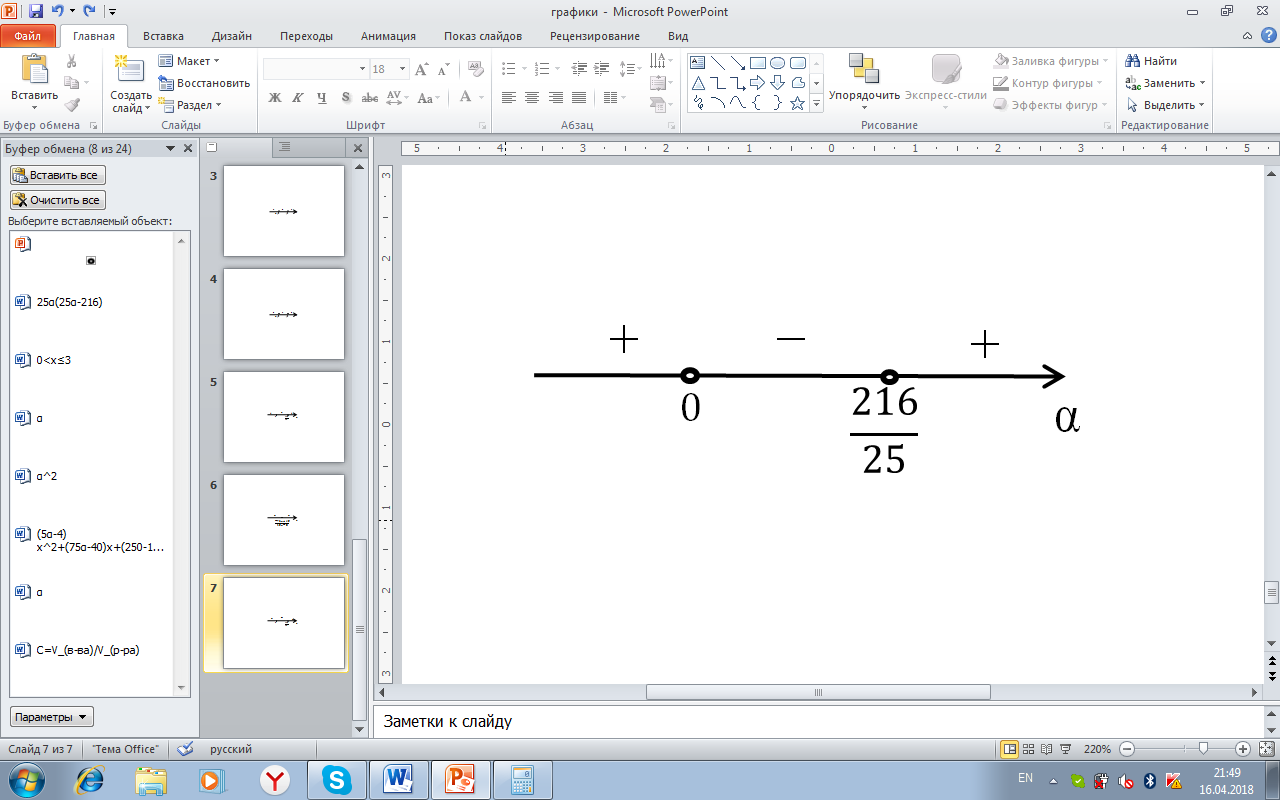
Рисунок1. Решение неравенства 25α(25α-216)<0

Условиям удовлетворяет только промежуток 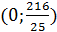, но учитывая условие 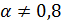, окончательным ответом будет .

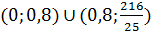При отрицательном дискриминантенеравенство (_*) не имеет корней. Так как значения α – положительные числа, 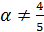, ветви параболы будут направлены вверх при 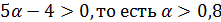. Следовательно, весь график выше оси Ох и х может принимать любые значения. Но в данном случае 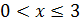. Если же 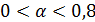, ветви параболы направлены вниз, и неравенство при данном Dне имеет решений.

2) D=0, следовательно, 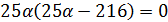. Корнями уравнения являются числа 0 и 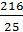. Но условию удовлетворяет только α= .

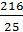В случае, когда D=0, неравенство будет иметь один корень: 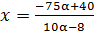. Заметим, что тогда 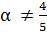. Решение неравенства при таких значениях изображено на рисунке 2:

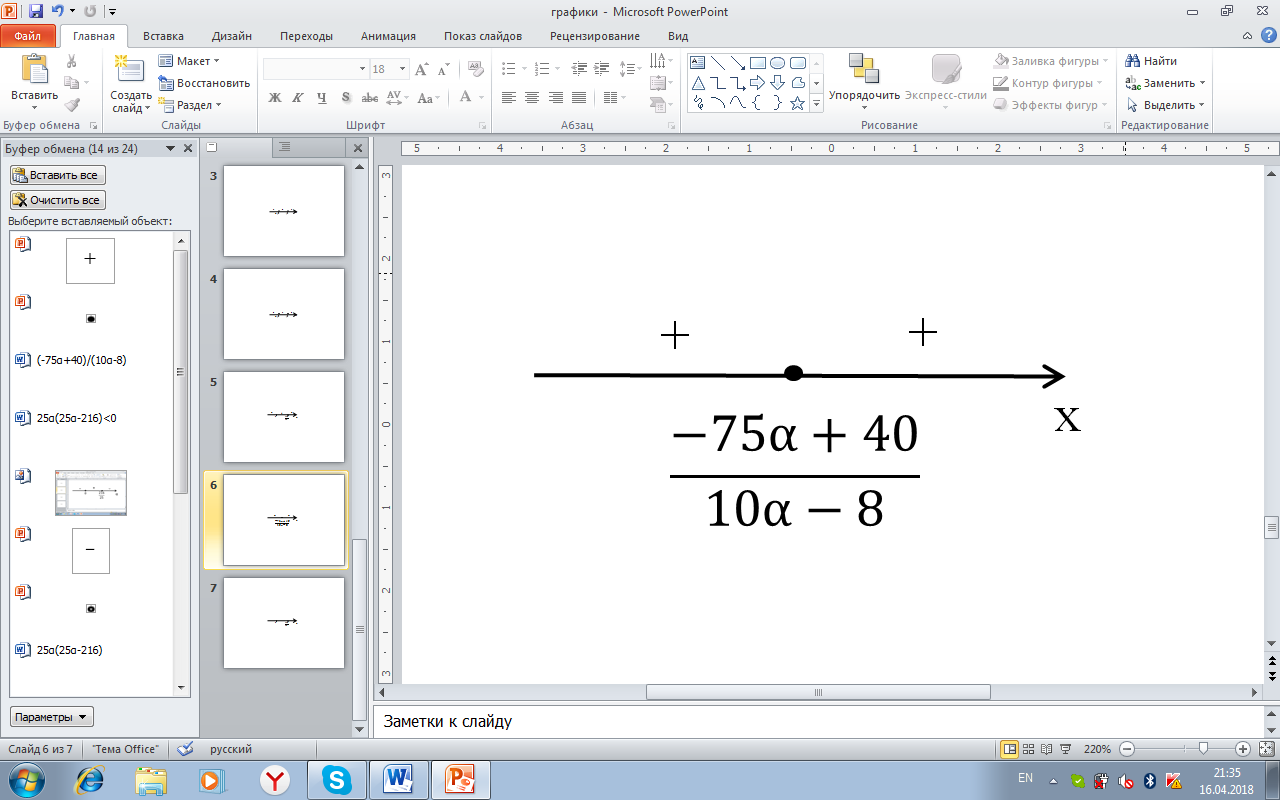
Рисунок 2. Решение неравенства 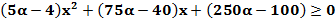при D=0

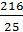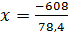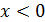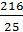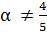Подставив значения параметра α= в выражение для х, получим , то есть . Получается, что при α= и значения х нет.

3) D>0, то есть 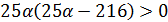. Решение данного неравенства показано на рисунке 3:

Рисунок3. Решение неравенства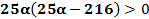

Условиям удовлетворяет интервал .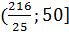

Тогда 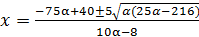, где 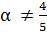. Но при подстановке значений параметра α в полученное выражение для х становится очевидно, что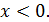

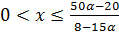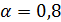Ответ: при и ;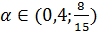

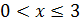, если .

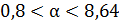2) Задачи на сплавы

Задачи на сплавы очень схожи с задачами на растворы, недаром их часто объединяют в один блок. В задачах такого типа обычно требуется найти массу или концентрацию.

Как и в предыдущем случае за х обозначаем искомую величину; параметр α, как правило, указан в условии. Основным ограничением, про которое нельзя забывать при решении, являются следующие условия:x и α не могут быть отрицательными (чаще всего просто положительными).

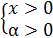При составлении выражений используется следующая формула: .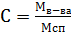

Рассмотрим примеры задач на составление уравнения и неравенства.

Задача4:

Имеются два куска сплава меди и цинка. Один из кусков содержит а% меди, другой – b%. В каком отношении нужно брать сплавы от первого и второго кусков, чтобы получить новый сплав, содержащий с%? При каких соотношениях между a, b, c решение задачи возможно и какую максимальную массу нового сплава можно получить, если масса первого куска Р г, а второго – Q г?[1, стр.357].

Решение:

При решении задач на сплавы и растворы, как правило, составляются таблицы, на основе данных которых потом составляются уравнения. Составим такую таблицу:

Сплав	Масса сплава, г	Концентрация меди, %
I сплав	P г	a%; 0,01*a г
II сплав	Q г	b%; 0,01*b г
III сплав	p+q г	c%; 0,01*c г

Пусть масса взятого куска первого сплав – p г, а второго – q г.

Данная задача решается при помощи уравнения, роль параметра в ней играют концентрации меди в начальных сплавах.

При составлении задач на сплавы, когда даны массы сплавов и концентрация вещества в них, пользуемся формулой: 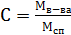, где M_в-ва=M_в-ва(1)+ M_в-ва(2)и M_сп(3)=М_сп(1)+ M_сп(2). Составим уравнение с использованием этой формулы: 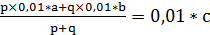. Решим данное уравнение:

; ;

; .

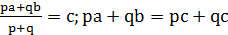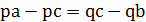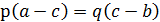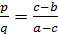Рассмотрим правую часть полученного уравнения. Так как отношение двух масс p и q величина всегда положительная, то и правая часть всегда больше нуля.

;
Числитель и знаменатель больше нуля	Числитель и знаменатель меньше нуля

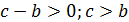
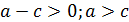
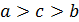
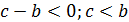
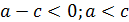
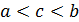
Для нахождения максимальной массы нового сплава следует рассмотреть отношения 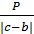и 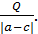Для этих соотношений существует три возможных случая:


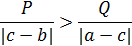
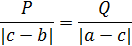
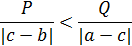
Максимальная масса		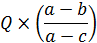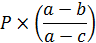или

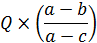
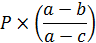
Теперь, рассмотрев все варианты, мы можем записать ответ.

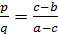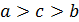Ответ: , при или .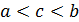

Если 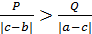, то m_max= 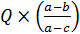; если 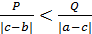, то m_max= 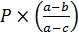; если 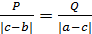, то m_max= 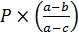или m_max= 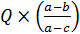[1].

Задача5:

Есть два куска сплава никеля со сталью. В первом сплаве, масса которого 8 кг, никеля содержится 2α, во втором сплаве массой 10 кг содержится α никеля. Какой массы должен быть кусок первого сплава, чтобы при его переплавке с первым куском никеля в новом сплаве было более60% никеля?

Решение:

Данная задача решается при помощи неравенства, роль параметра в ней играет концентрация никеля в исходных сплавах.

Приняв массу куска второго сплава, который нужно добавить, за x кг, можно записать массу никеля в новом сплаве: 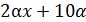. Тогда масса нового сплава равна 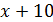кг. Подставляя данные выражения в формулу 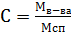, получаем концентрацию никеля в новом сплаве. По условию задачи,данная величина должна быть более60%, то есть 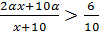.Перед решением рассмотрим, какие значения может принимать α и х: 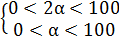, то есть 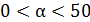и 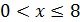. Теперь можно приступить к решению неравенства, приводя слагаемые к общему знаменателю и используя свойство неравенства о сохранении знака:

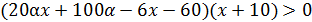
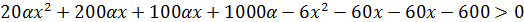
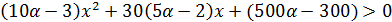– обозначим это неравенство (_*).

I. При 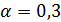неравенство (_*) принимает вид 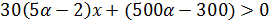, 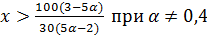.Так как х>0, то выражение 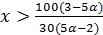будет верно, когда 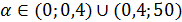. При этом величина xне превосходит 8: .

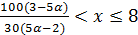II. При α≠0,3 неравенство является квадратным. Найдём значение дискриминанта уравнения 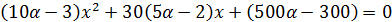, воспользовавшись формулой :

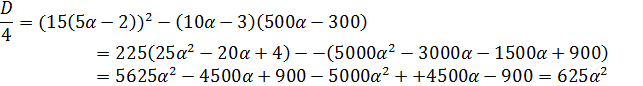
Теперь рассмотрим случаи, когда положителен, отрицателен, равен 0.

1) 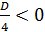, то есть 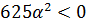. Корень этого уравнения 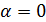[рис.4].

Рисунок4. Решение неравенства 625α²<0

У этого неравенства нет корней, следовательно, значений не существует. Тогда не существует и значений х, так как х должен выражаться через .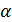

2) 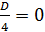, то есть 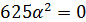. Корнем уравнения равняется 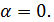Но исходя из условий, 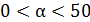. Следовательно, и в этом случае не существует значений х и 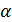, удовлетворяющих условиям.

3) 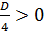, то есть 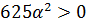[рис.5].

Рисунок5. Решение неравенства 625α²>0

Условиям задачи удовлетворяет .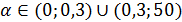

Тогда 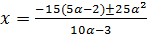. Нанесём корни на координатную прямую. Если 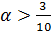, то ветви параболы 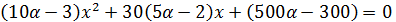будут направлены вверх, решение данного неравенства показано на рисунке 6:

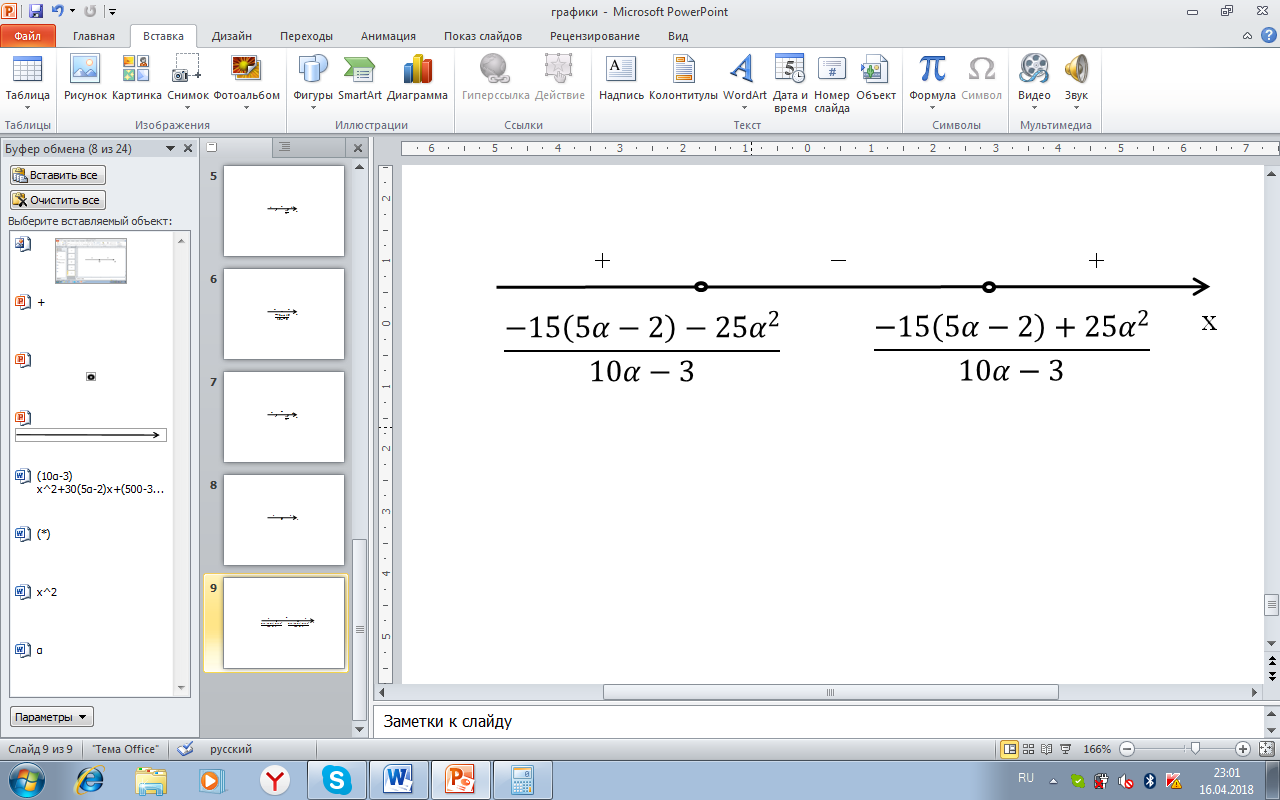
Рисунок6. Решение неравенства (10α-3)x²+30(5α-2)x+(500α-300)>0 при D>0

Условиям удовлетворяет интервал 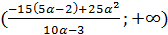, но при этом 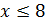. Следовательно, нужно проверить условие 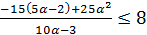; решение его изображено на рисунке 7.

→ ,

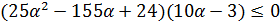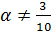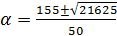
Рисунок7. Решение неравенства (-15(5α-2)+25α²)/(10α-3)≤8

Тогда .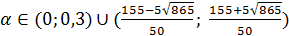

Ответ: 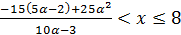, если ;

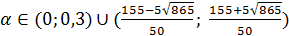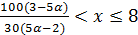при .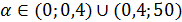

Задачи на движение

В задачах на движение за переменную следует брать искомое значение: скорость, время или расстояние. Главное, о чём ни в коем случае нельзя забывать при решении такого типа задач, что значения переменной не могут быть отрицательными (х≥0), значения параметра тоже (в случае, когда параметр обозначает время, α>0).

Задача6:

Две точки движутся по сторонам прямоугольного треугольника, начиная с вершины прямого угла. С какой скоростью должна двигаться вторая точка, чтобы спустя время t расстояние между ними было не менее 20 м, если известно, что скорость первой точки на 5 м/с больше?

Решение:

Данная задача решается при помощи неравенства, роль параметра в ней играет время движения.

Примем искомую скорость V₂второй точки за х м/с, тогда скорость V₁первой точки равна (х+5) м/с. Теперь можно найти расстояние, которое прошла каждая точка за время t: xt м и (х+5)t м. Учтём, что t>0, x≥0.

Расстояние между их положением находится по формуле 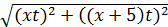. Причём полученное выражение должно быть не менее 20 м, то есть 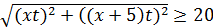. Решим полученное неравенство:

; ;

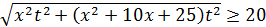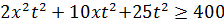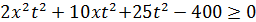Найдём значение дискриминанта уравнения 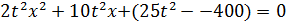. Применим формулу :

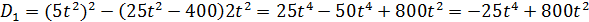
Рассмотрим возможные случаи.

1) Если D₁<0, то неравенство корней не имеет, а так как ветви параболы направлены вверх, все значения х будут положительны. Теперь найдём значения параметра t[рис.8].

; ; .

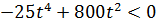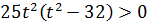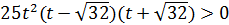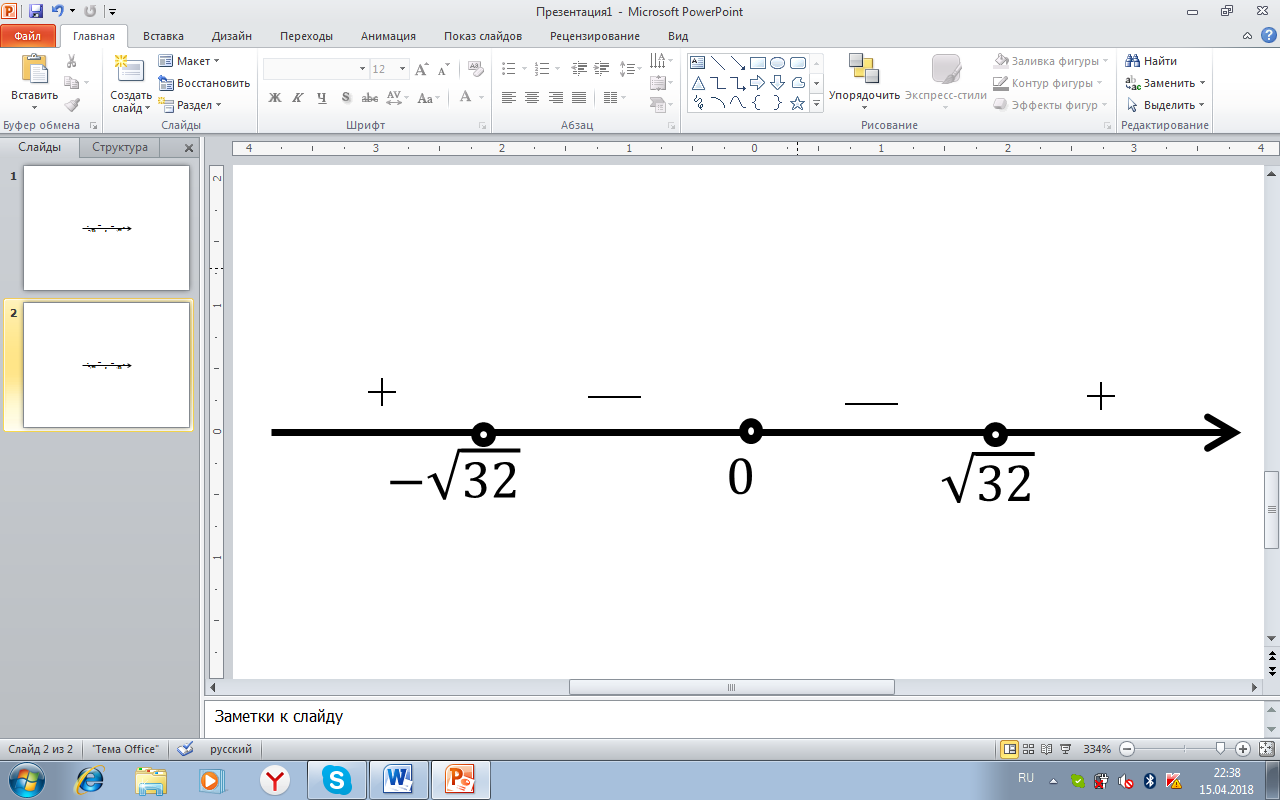
Рисунок8. Решение неравенства -25t⁴+800t²<0

Условию удовлетворяет интервал ( 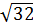; +∞) (по-другому, t> 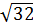), т.к.t>0.

2) Неравенство имеет решение при D₁=0, то есть 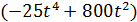=0

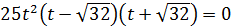→t₁=0; t₂= 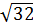; t₃=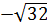

Удовлетворяет условиям только t= .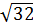

Теперь найдём значение х, подставив значение параметра tв уравнение 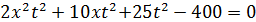. Получим:

; ;

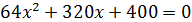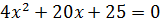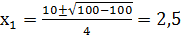3) Неравенство 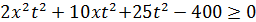имеет решения при D₁>0, то есть 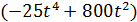>0.

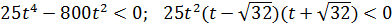Решим уравнение 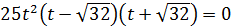[рис.9]. Получим следующие корни: t=0, t= 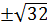. Нанесём данные корни на координатную прямую и определим знаки, выколов точку 0, так как время – величина положительная:

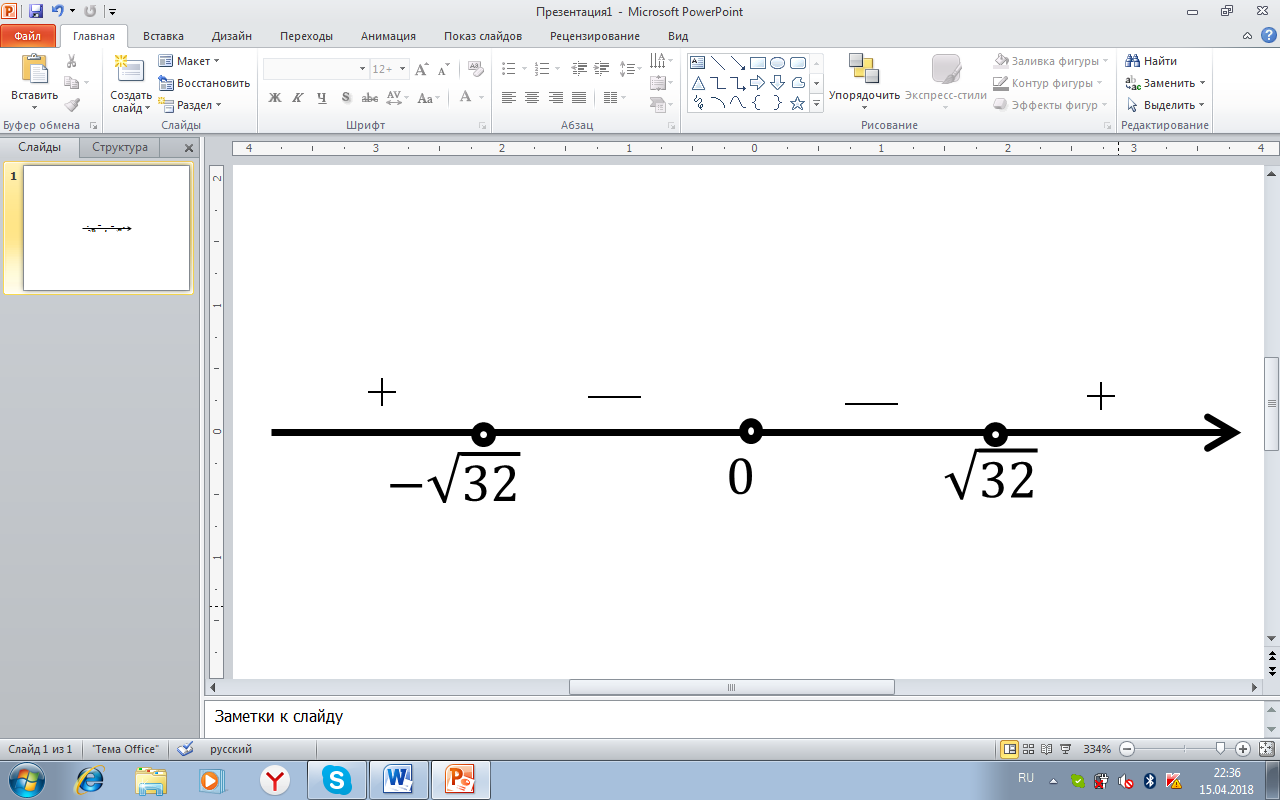
Рисунок9. Решение неравенства 25t²(t-√32)(t+√32)<0

Условию удовлетворяет полуинтервал (0; 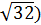(по-другому, 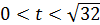). Тем самым мы нашли область допустимых значений параметра для данного случая. Теперь найдём значение х:

Так как 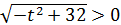, то и 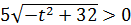. Следовательно, удовлетворять условию х>0 будет только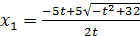

Ответ:х – любое положительное число, если t> 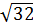; х= 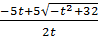, если 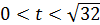; х=2,5, если t= .

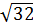Задача7:

Из города А в город В, расстояние между которыми равно 2S км, выехал мотоциклист. Спустя время t из этого же города выехал автомобилист, нагнавший мотоциклиста на расстоянии L от города А. Он доехал до В, развернулся и на расстоянии L уже от города В вновь встретил мотоциклиста. При этом в город А он вернулся позже, чем мотоциклист доехал до В. Какова разница во времени их прибытия?

Решение:

Сложность в решении данной задачи заключается в том, что не дано численных значений. Так как в задачах на движение основной является формула связи между расстоянием, временем и скоростью, за значение параметра следует принять расстояние между городами, то есть 2S. Задача решается при помощи составления уравнений.

В данной задаче целесообразнее за переменные обозначить скорости мотоциклиста и автомобилиста. Пусть x км/ч – скорость мотоциклиста, а yкм/ч –скорость автомобилиста.

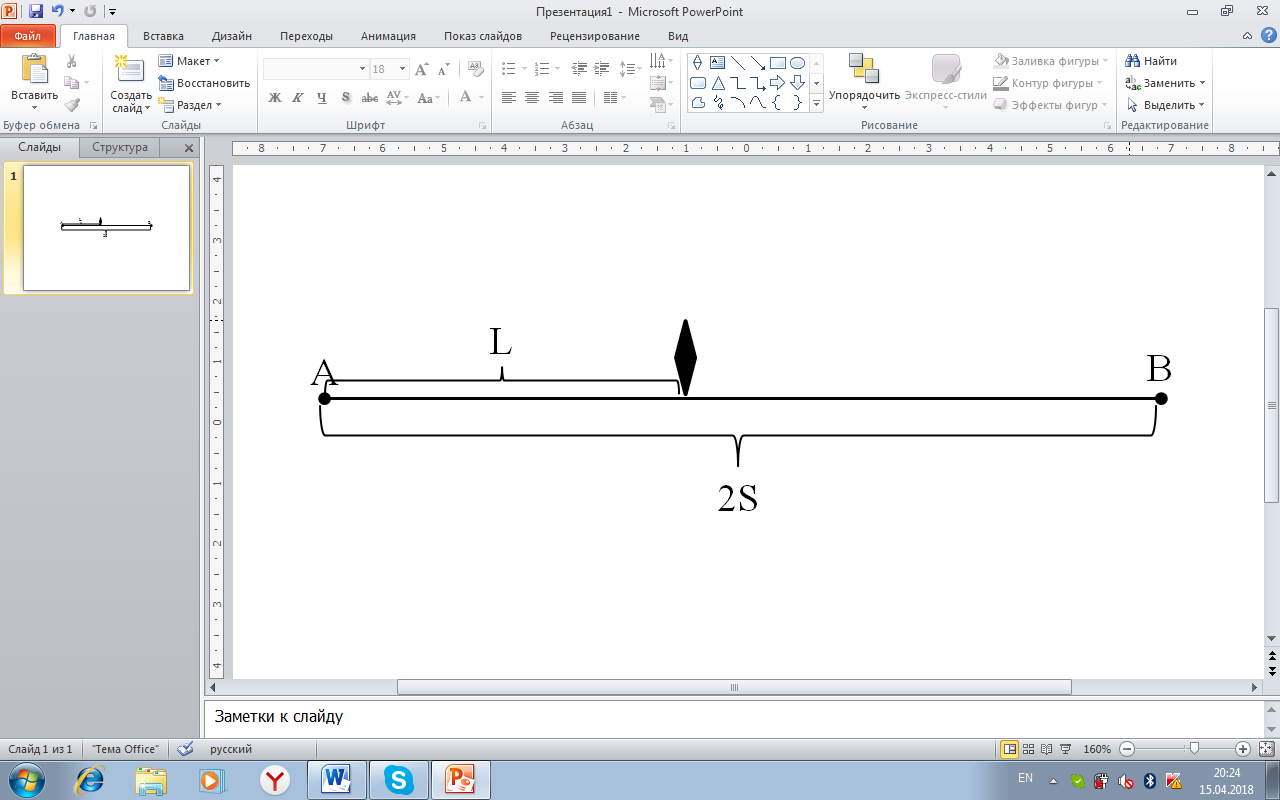
Рисунок10. Пройденный автомобилистом и мотоциклистом путь до первой встречи

До встречи они оба преодолели расстояние L[рис.10], то есть и соответственно. При этом автомобилист выехал позже на время t, поэтому можно составить уравнение: 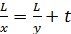. Обозначим это уравнение (1).

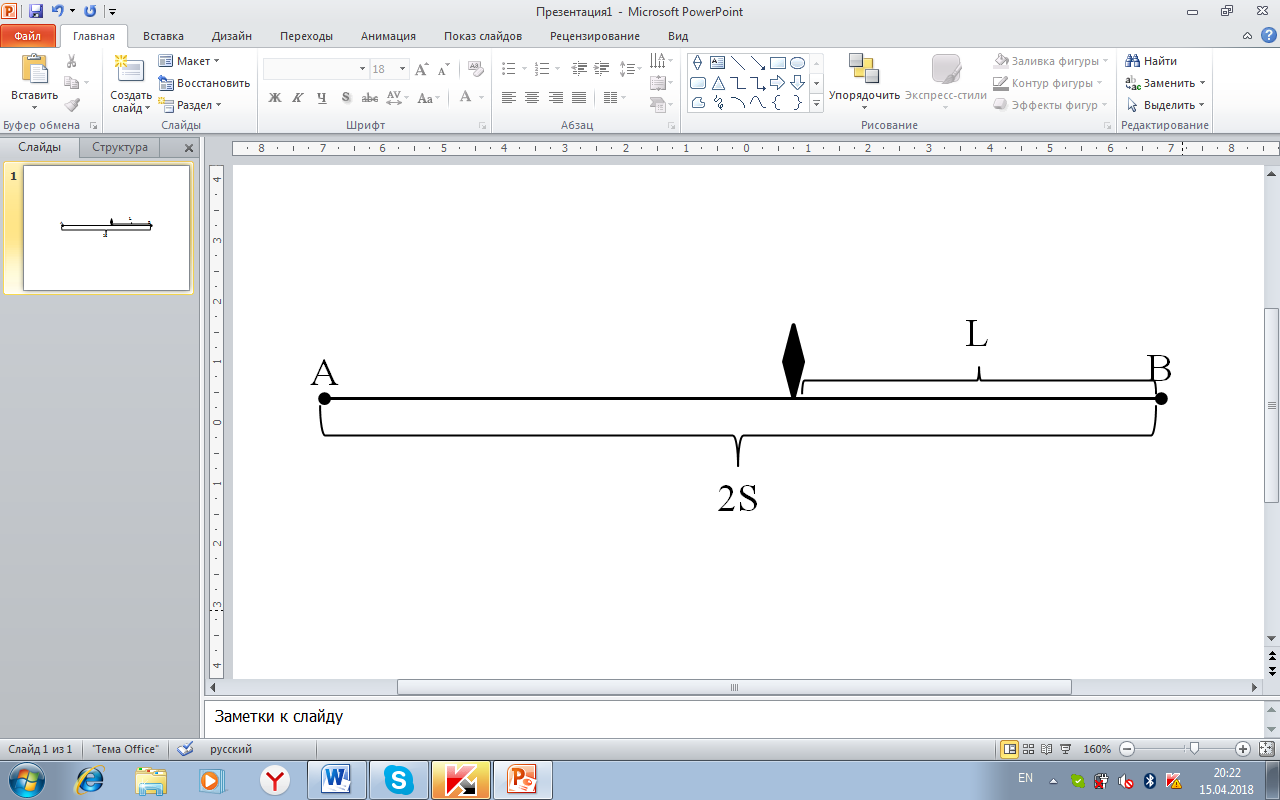
Рисунок11. Расстояние, на котором от пункта В встретились мотоциклист и автомобилист

Во время второй встречи на расстоянии L от пункта В автомобилист провёл в дороге 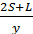времени, в то время как мотоциклист – 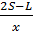, их путь изображён на рисунке 11.При этом разница во времени, проведённом в пути –t, поэтому 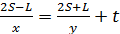. Обозначим это уравнение за (2).

Всё время мотоциклиста в пути равнялось 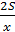, а всё время пути автомобиля – 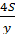. Получается, что ответом на вопрос задачи станет величина, равная .

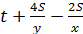Для нахождения данной величины рассмотрим уравнения: 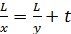; 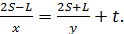Видно, что если умножить первое уравнение на (L–2S), а второе – на L, то в итоге получим: 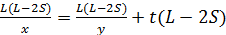и 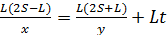. При сложении двух полученных уравнений левая часть будет равна 0, а после преобразований получим: 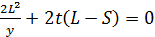. Выразим уз полученного уравнения 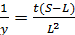. Теперь преобразуем уравнение (1), разделив обе части на L: 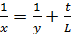. Подставив в это уравнение, получим 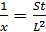. Получив и , можем ответить на вопрос задачи: .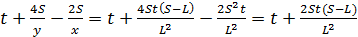

Теперь необходимо проверить область значений параметра 2S. Исходя из условия задачи, 2S–2L>0, то есть . Кроме того, 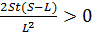, так как время tзаведомо больше 0, а разница во времени может быть только числом положительным. Получается, 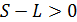, то есть .

Ответ: 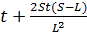, если .

Дата добавления: 2018-06-27; просмотров: 2548; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!
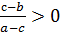