Описать метод ветвей и границ
Данный метод позволяет отбрасывать достаточно большие подмножества допустимого множества D, состоящие из заведомо неоптимальных точек. Рассмотрим задачу ЦЛП:
Р= сх 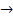 max, (1)
max, (1)
Ax  b, (2)
b, (2)
x  0, (3)
0, (3)
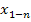 - целые. (4)
- целые. (4)
На первом этапе решаем «родительскую» задачу ЛП – задачу (1)-(3), но без учёта целочисленности (4), или требования целочисленности. Если её реш-ие целое, то оно и явл-ся реш-ем задачи (1) – (3). В противном случае выбираем любую нецелочислен компоненту, например 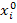 . Далее разбиваем исходную задачу на 2 с помощью след дополнит ограничений:
. Далее разбиваем исходную задачу на 2 с помощью след дополнит ограничений: 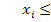 [
[ 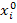 ], (5)
], (5)
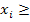 [
[ 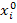 ]+1, (6)
]+1, (6)
где [ 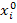 ] – целая часть числа
] – целая часть числа 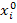 .
.
Задачи (1) – (3), (5) и (1) – (3), (6) наз-ся «дочерними» задачами. Существен св-во процесса ветвления сост в том, что объединение допустимых множеств «дочерних» задач строго меньше допустимого множества «родительской» задачи, в то же время объединение допустимых множеств «дочерних» задач с учётом целочисленности в точности равно допустимому множеству «родительской» задачи с учётом целочисленности. Добавляемые ограничения представляют собой отсекающие плоскости, т.е оптимальное решение «родит» задачи не удовлетворяет каждому ограничению (5), (6). После «дочерних» задач решаем либо их обе, либо какую-то одну из них и продолжаем процесс ветвления.
Критерии окончания ветвления:
В задаче на максимум в начале решения граничное значение целевой функции, или рекорд, полается равным -∞.
|
|
|
1. Получена задача, не имеющая решения. Это становится все более вероятным с увеличением глубины ветвления, когда все большее число ограничений вида (5) или (6) добавляется к уже существующим ограничениям ( так, что все более вероятным становится несовместимость системы ограничений получаемых задач).
2. Если находится новое целочисленное решение, то оно сравнивается с рекордом; если прежний рекорд превзойден, то запоминается новый рекорд, в противном случае остается старый.
3. Получаемое оптимальное нецелочисленное решение задачи на какой-то стадии ветвления сравнивается с рекордом; если это значение меньше, чем рекорд, то ветвление задачи прекращается, так как нет возможности побить рекорд.
Непобитый рекорд дает оптимальное решение исходной задачи ЦЛП.
Метод динамического программирования, функция состояния, уравнение Беллмана
Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге.
|
|
|
В основе динамического программирования лежат 2 принципа:
Первый- принцип оптимальности Беллмана: каковы бы ни были начальное состояние системы и принятое решение, все последующие решения на остальных шагах должны составлять оптимальную стратегию относительно состояния, возникающего в результате первого решения.
Второй- принцип вложения: природа задачи, допускающая использование метода динамического программирования, не меняется при изменении числа шагов.
Структура процессов, исследуемых методом динамического программирования, должна удовлетворять следующим условиям:
· небольшое число переменных
· * управляемый процесс- Марковский, т.е. предыстория не имеет значения при определении будущих действий
· * критерий эффективности J является аддитивным.
Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.
|
|
|
72. Составить математическую модель и записать функциональное уравнение Беллмана (рекуррентное соотношение), расшифровать все переменные и функции, входящие в него для следующей задачи:
Предприятие производит некоторое изделие, на которое оно имеет заказ на п месяцев.
Необходимо спланировать объем выпуска 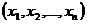 и хранения
и хранения 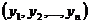
продукции для каждого месяца его работы при условии, что суммарные затраты на производство и хранение продукции за п месяцев будут минимальными при полном удовлетворении спроса на продукцию. При этом уровень запасов к началу первого месяца 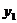 задан, а к концу последнего
задан, а к концу последнего 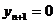 . Известны также спрос
. Известны также спрос 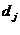 на продукцию в каждом j-м месяце и затраты
на продукцию в каждом j-м месяце и затраты 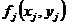 на производство
на производство 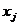 и хранение
и хранение 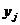 единиц продукции в каждом j-ммесяце.
единиц продукции в каждом j-ммесяце.
F(x1, x2, x3, x4) =f1(x1) + f2(x2) + f3(x3) + f4(x4)
|
|
|
x1+x2+x3+x4= Z(700)
gk= max( fk(xk) + gk-1 (Z-xk)) F= g4(Z)
xk= 0, 100, 200, 300, 400
| G3 F3 | 0 100 200 300 400 |
| 0 100 200 300 400 | 95 97 105 101 99 |
g3(400) =105
73.Составить математическую модель и записать функциональное уравнение Беллмана
(рекуррентное соотношение), расшифровать все переменные и функции, входящие в него
для следующей задачи:
Предполагается, что 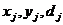 принимают целые неотрицательные значения.
принимают целые неотрицательные значения.
2). Пусть требуется загрузить в самолет грузоподъемностью W тоннгруз, состоящий из предметов п различных типов, таким образом, чтобы стоимость всего груза была
максимальной. Для каждого предмета j-го типа, j= 1,2,. . . ,п, заданы вес 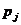 в тоннах и
в тоннах и
стоимость 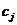 в тысячах рублей одного предмета этого типа, где все
в тысячах рублей одного предмета этого типа, где все 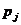 и
и 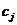 -целые
-целые
положительные числа. Причем предметов каждого типа можно загружать в самолет по несколько штук.
Ур-ние Беллмана: Fk*(ξ) = max {fk (xk) + Fk-1(ξ-xk)} = fk( 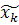 ) + F(ξ-
) + F(ξ- 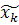 )
)
0 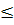 xk
xk 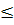 ξ xk
ξ xk
0 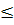 ξ
ξ 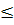 b
b
Fk*(ξ) – max приращение прибыли по k предприятиям.
74.Составить математическую модель и записать функциональное уравнение Беллмана
(рекуррентное соотношение), расшифровать все переменные и функции, входящие в него
для следующей задачи:
Средства в размере b млн. рублей распределяются между п предприятиями в количествах,
кратных а млн. руб., причем 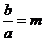 - целое число. При выделении j-му предприятию
- целое число. При выделении j-му предприятию 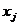 млн. рублей оно приносит доход
млн. рублей оно приносит доход 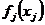 млн. рублей.Требуется распределить выделенные средства так, чтобы суммарный доход по всем предприятиям был максимальным.
млн. рублей.Требуется распределить выделенные средства так, чтобы суммарный доход по всем предприятиям был максимальным.
Ур-ние Беллмана: Fk*(ξ) = max {fk (xk) + Fk-1(ξ-xk)} = fk( 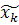 ) + F(ξ-
) + F(ξ- 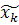 )
)
0 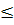 xk
xk 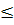 ξ xk
ξ xk
0 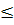 ξ
ξ 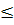 b
b
Fk*(ξ) – max приращение прибыли по k предприятиям.
Обозначим через 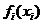 прирост мощности или прибыли на i-м предприятии, если оно получит
прирост мощности или прибыли на i-м предприятии, если оно получит 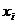 рублей капитальных вложений. Требуется найти такое распределение
рублей капитальных вложений. Требуется найти такое распределение 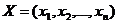 капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли
капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли
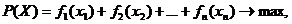 при ограничении по общей сумме капитальных вложений
при ограничении по общей сумме капитальных вложений 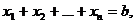 причем будем считать, что все переменные
причем будем считать, что все переменные 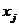 принимают только целые неотрицательные значения:
принимают только целые неотрицательные значения: 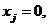 или
или 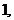 или
или 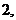 или
или 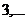
Функции 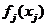 мы считаем заданными, заметив, что их определение – довольно трудоемкая экономическая задача. Введем параметр состояния и определим функцию состояния. За параметр состояния
мы считаем заданными, заметив, что их определение – довольно трудоемкая экономическая задача. Введем параметр состояния и определим функцию состояния. За параметр состояния 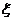 примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния
примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния 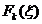 определим как максимальную прибыль на первых
определим как максимальную прибыль на первых 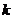 предприятиях, если они вместе получают
предприятиях, если они вместе получают 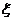 рублей. Параметр
рублей. Параметр 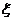 может изменяться от
может изменяться от 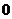 до
до 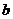 . Если из
. Если из 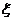 рублей
рублей 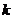 -е предприятие получит
-е предприятие получит 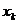 рублей, то каково бы ни было это значение, остальные
рублей, то каково бы ни было это значение, остальные 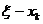 рублей естественно распределить между предприятиями от первого до
рублей естественно распределить между предприятиями от первого до 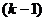 -го так, чтобы была получена максимальная прибыль
-го так, чтобы была получена максимальная прибыль 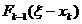 . Тогда прибыль
. Тогда прибыль 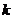 предприятий будет равна
предприятий будет равна 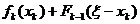 . Надо выбрать такое значение
. Надо выбрать такое значение 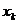 между
между 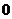 и
и 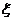 , чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению
, чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению 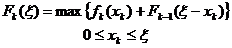 для
для 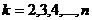 . Если же
. Если же 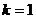 , то
, то 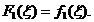 (при условии, что функция
(при условии, что функция 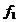 возрастающая).
возрастающая).
75. Составить математическую модель и записать функциональное уравнение Беллмана
(рекуррентное соотношение), расшифровать все переменные и функции, входящие в него
для следующей задачи:
Предприятие может производить п видов изделий, располагая некоторым ресурсом в объеме
b единиц (b - целое положительное число). Известны затраты ресурса 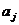 на изготовление
на изготовление
одного изделия j-го вида, а также известна ожидаемая прибыль сj от реализации одного
изделия j-го вида ( 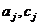 . - целые положительные числа), j = 1, 2,..., п.
. - целые положительные числа), j = 1, 2,..., п.
Требуется составить план выпуска изделий, максимизирующий суммарную прибыль.
76. Составить математическую модель и записать функциональное уравнение Беллмана
(рекуррентное соотношение), расшифровать все переменные и функции, входящие в него
для следующей задачи:
Пусть п предприятиями некоторого объединения должен быть произведен определенный
продукт в количестве bединиц. При изготовлении хj единиц продукта на j-м предприятии
издержки составляют 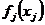 денежных единиц. Требуется спланировать производство
денежных единиц. Требуется спланировать производство
Дата добавления: 2018-06-01; просмотров: 361; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
