Записать алгоритм решения транспортной задачи (перечислить по порядку этапы решения). Обосновать конечность метода потенциалов решения транспортной задачи.
1 Строится какое-нибудь базисное решение
2 Для построенного базисного решения рассчитываются потенциалы
3 Рассчитанные потенциалы для расчета оценочных коэффициентов ∆ij . Если все ∆ij ≤0, то задача решена и построенное базисное решение оптимально.
4 Если среди ∆ij >0, то выбирается положительный коэффициент, обычно, но не обязательно, max по величине и с помощью циклов пересчета строиться новое базисное решение, для которого повторяются пункты 2-3.
Конечность метода потенциалов – метод потенциалов всегда приводит к оптимальному плану
Объяснить смысл перевозок от фиктивного поставщика или к фиктивному потребителю в оптимальном решении транспортной задачи.
Для сведения открытой задачи к закрытой вводятся фиктивные пункты производства или потребления. Если суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, вводится фиктивный потребитель, у которого объем потребления равен разнице между объемом производства и объемом потребления; если же суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, то вводится фиктивный поставщик.
Обозначим через хij количество груза, планируемого к перевозке от i-го поставщика j-му потребителю. При наличии баланса производства и потребления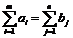 
математическая модель транспортной задачи будет выглядеть так: найти план перевозок
|
|
|
Х = (хij), 
; 
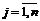
минимизирующий общую стоимость всех перевозок 
при условии, что из любого
пункта производства вывозится весь продукт: 
и любому потребителю доставляется необходимое количество груза 
, причем по смыслу задачи х11 > 0 ,. . . ., xmn > 0.
поставки от фиктивного поставщика укажут объем неудовлетворенного спроса соответствующих потребителей, а поставки к фиктивному потребителю – остатки продукта у поставщиков.
Что такое целочисленное линейное программирование? Допустимое множество задачи ЦЛП.
К задачам ЦЛП относят задачи с линейной целевой функцией и линейными ограничениями, в которых на все переменные наложены условия целочисленности. Допустимое множество задачи ЦЛП или конечно, или состоит из множества изолированных точек.
Что такое параметрическое линейное программирование? Где может находиться параметр?
Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров. Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, что-бы в результате решения иметь наилучшие планы для любого варианта исходных данных. С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения. Заметим, что существуют различные подходы к подобному анализу (например, на основе постановки двойственной задачи). Здесь мы, не ссылаясь на двойственные оценки, рассмотрим самые простейшие варианты решения для самых простейших параметрических программ. 1) Коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ (времени, температуры и т. п.). 2)В случае зависимости от параметра компонент вектора правых частей ограничений, т. е. решения задачи поиска экстремума функции
|
|
|
Дата добавления: 2018-06-01; просмотров: 454; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!