Примеры решения задач по теме« Выборочное наблюдение»
Понятие выборочного наблюдения, виды и методы расчета ошибок репрезентативности, правила выбора формул для расчета ошибок выборочной средней и выборочной доли альтернативного признака рассмотрены на стр. 38- 43 данного пособия.
Пример 10 - Определение пределов генеральной средней и генеральной доли альтернативного признака
Для изучения распределения работников бюджетной сферы по размерам заработной платы в городе проведено 10%- ное выборочное обследование. В результате учета 900 человек выявлено, что средняя зарплата работников составляет 32500 руб. со средним квадратическим отклонением 4200 руб. Из числа работающих 15% получают зарплату свыше 40 000 руб.
Требуется с вероятностью 0,954 определить пределы среднего размера заработка одного работника бюджетной сферы в городе и пределы доли работников, получающих свыше 40000 руб.
Решение:
В данном примере требуется определить пределы двух величин: среднего значения признака и доли жителей, получающих свыше 40000 руб.
Для исчисления пределов вначале следует рассчитать предельные ошибки выборочной средней и выборочной доли альтернативного признака.
Обозначим символами приведенные в условии цифровые данные.
• Так как объем выборки – 10%, следовательно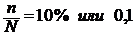 
;
• Учтено 900 человек, т.е. n= 900;
• Средняя зарплата работника - 32500 руб., т.е.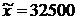 
;
• Среднее квадратическое отклонение – 4200, значит, 
;
• 15% работающих получают свыше 40000, следовательно, доля альтернативного признака -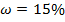 
или 0,15;
|
|
|
• Вероятность расчетов F(t) – 0,954, следовательно, t = 2.
На первом этапе определим среднюю ошибку выборочной средней. Так как в условии не оговаривается, повторный или бесповторный отбор применялся при обследовании, по умолчанию предполагается бесповторный отбор. Объем выборки - 10%, следовательно, для расчета средней ошибки выборочной средней используем формулу (9.5):
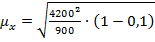=132,8
Определим предельную ошибку выборочной средней, исходя из соотношения:
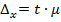
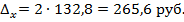
Пределы средней заработной платы работников госсектора определим по формуле:
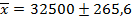
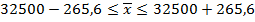
Следовательно, с вероятностью 0,954 (т.е. в 954 случаях из 1000) мы можем утверждать, что средняя зарплата работников госсектора в городе будет не меньше чем 32234,4 руб. и не превысит 32765,6 руб.
На втором этапе определим ошибку доли альтернативного признака.
Начнем с расчета средней ошибки на основе формулы (9.6), так как отбор бесповторный объемом более 5%:
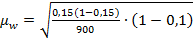=0,0113
Предельная ошибка доли альтернативного признака при вероятности расчетов 0,954 определим, исходя их формулы:
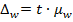
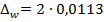
Пределы доли работников госсектора, получающих зарплату свыше 40000 руб., в генеральной совокупности находятся по формуле:
|
|
|
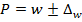
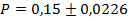
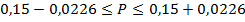
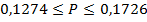
Или, если перевести результаты в процентные соотношения,
. 
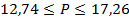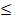
Следовательно, доля работников госсектора, получающих зарплату свыше 40000 руб., колеблется от 12,74% до 17,26%, что можно утверждать с вероятностью 0,954.
Дата добавления: 2018-06-01; просмотров: 2811; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!