Примеры решения задач по теме« Средние величины и показатели вариации»
Виды средних величин и показателей вариации, а также формулы их расчета с пояснением принципов выбора вида и формы показателя приведены на стр. 18-23 данного пособия.
Пример 5- Расчет среднейвеличины в интервальных рядах распределения
В таблице 7 приведены условные данные о распределении предприятий по объему продаж:
Таблица 7- Условные данные о распределения предприятий по объему продаж
| Объем продаж, тыс. руб. | Количество предприятий, шт. |
| до 100 | 2 |
| 100-140 | 15 |
| 140-180 | 10 |
| свыше 180 | 4 |
Определите средний объем продаж в расчете на одно предприятие.
Решение:
При расчете среднего значения признака в интервальных вариационных рядах используется средняя арифметическая взвешенная, определяемая по формуле (5.2), приведенной в таблице 3:
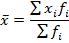
В формуле в качестве значения признака 
используется дискретное число, однако в приведенном примере значение признака приводится в виде интервала. В этом случае за принимается середина каждого интервала, определяемая как полусумма максимального и минимального значения признака в группе.
Например, если группировочный интервал 8-10, за будет принято число 9, так как полусумма максимального и минимального значения признака в группе будет определена следующим образом:
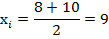
При наличии открытых интервалов, у которых определена только одна граница – верхняя или нижняя, открытый интервал принимается равным по величине смежному с ним закрытому интервалу.
|
|
|
У первой группы имеется открытый интервал, в котором указана только верхняя граница. В нашем случае, он принимается равным по величине второму интервалу, т. е. считается, что у первой группы объем продаж составит от 60 до 100 тыс. руб. Серединой интервала в данном случае будет объем продаж, равный 80 тыс. руб. (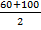 
).
Открытый интервал у последней группы принимается равным по величине предшествующему интервалу, т. е. примет значения от 180 до 220 тыс. руб., а середина интервала будет рассчитана (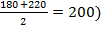 
)
Средний объем продаж по данной совокупности определим так:
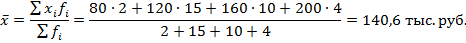
Пример 6 - Расчет средней, показателей вариации, моды и медианы в интервальном вариационном ряду распределения
Имеются данные о затратах времени на изготовление деталей в 200 отраслях:
Таблица 8 -Условные данные о затратах времени на изготовление деталей
| Время, затраченное на изготовление 1 детали, мин. | Число деталей, штук | Сумма накопленных частот, Si |
| 1 | 2 | 3 |
| 8-10 | 14 | 14 |
| 10-12 | 26 | 40 |
| 12-14 | 75 | 115 |
| 14-16 | 40 | 155 |
| 16-18 | 20 | 175 |
| 18-20 | 15 | 190 |
| 20-22 | 10 | 200 |
| Итого | 200 | Х |
По приведенным данным вычислите:
1. Среднее значение варьирующего признака;
|
|
|
2. Показатели вариации: размах, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициенты вариации и осцилляции;
3. Моду и медиану.
Решение:
Задачи данного типа рекомендуется решать в табличной форме. За значение признака ( ) принимаются середины интервалов, методика определения которых рассмотрена в предыдущем примере.
Определим среднее значение признака по формуле средней арифметической взвешенной (5.2), подставляя данные из гр. 3 и 2 таблицы 9:
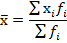
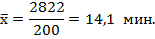
Таблица 9 - Расчетная таблица
| xi | fi | xifi | 
| 
|  
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 9 | 14 | 9 · 14 = 126 | |9 - 14,1| = 5,1 | 5,1 · 14 = 71,4 | 5,12 · 14 = 364,14 |
| 11 | 26 | 11 · 26 = 286 | |11 - 14,1| = 3,1 | 3,1 · 26 = 80,6 | 3,12 · 26 = 249,86 |
| 13 | 75 | 975 | 1,1 | 82,5 | 90,75 |
| 15 | 40 | 600 | 0,9 | 36,0 | 32,40 |
| 17 | 20 | 340 | 2,9 | 58,0 | 168,20 |
| 19 | 15 | 285 | 4,9 | 73,5 | 360,15 |
| 21 | 10 | 210 | 6,9 | 69,0 | 476,10 |
| Итого | 200 | 2822 | 24,9 | 471,0 | 1741,60 |
Размах вариации рассчитываем как разницу между серединами первого и последнего интервалов:
R = 21 - 9 = 12 мин.
Среднее линейное отклонение определяется по формуле (5.14):
Среднее квадратичное отклонение определим по формуле (5.16):
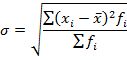
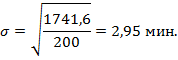
данные для расчета дисперсии содержатся в графах 2 и 6 таблицы 9. В данном примере она определяется по формуле (5.18):
|
|
|
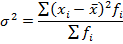
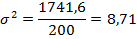
коэффициент вариации определяем, подставляя данные в формулу (5.22):
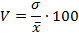
Коэффициент осцилляции в нашем примере определяется по формуле (5.20) и он равен:
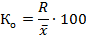
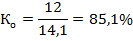
2. Чтобы определить моду в данном интервальном ряду распределения, воспользуемся формулами (5.10):
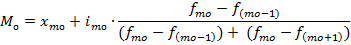
Вначале определяют модальный интервал, т.е. интервал, имеющий наибольшую частоту. В данном примере модальным является интервал 12-14 минут, т.к. его частота составляет 75 единиц.
Нижняя граница модального интервала (хмо) составит 12, величина модального интервала (iмо) = 2, частота модального интервала (fмо) = 75, частота интервала, предшествующего модальному (f(мо-1)) = 26, частота интервала, следующего за модальным (f(мо+1)) = 40. Следовательно, мода равна:
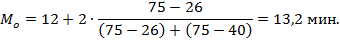
Для определения медианы в интервальном ряду распределения воспользуемся формулой (5.11):
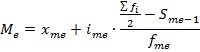
Найдем медианный интервал. У медианного интервала сумма накопленных частот должна быть равна половине суммы всех частот ряда или превышать эту величину. В нашем примере сумма всех частот равна 200 единицам, полусумма - 100 единиц (200 : 2).
|
|
|
В гр. 3 таблицы 8 рассчитываются суммы накопленных частот последовательным сложением частот каждой группы. Для первой группы сумма накопленных частот - 14 единиц, для второй - 40 (14+26), для третьей - 115 (14 + 26 + 75) и т.д.
В третьей группе сумма накопленных частот впервые превысит полусумму всех частот ряда (115 больше 100), следовательно, третья группа является медианной, а медианный интервал - 12-14 мин. тогда медиана равна:
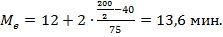
Вывод. из приведенных расчетов видно, что среднее время на изготовление 1 детали составит 14,1 мин., при этом половина рабочих затратит на изготовление 1 детали в среднем не более 13,6 мин. (Ме = 13,6), а самая многочисленная группа затратит на изготовление 1 детали в среднем 13,2 мин.
Индивидуальное время на изготовление 1 детали отклоняется от среднего времени в среднем на 2,9 мин. (σ = 2,95), что составляет 20,9% (V = 20,9). Средняя типична для совокупности, т.к. коэффициент вариации не превышает 30%.
Дата добавления: 2018-06-01; просмотров: 13091; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!