Признак параллельности прямой и плоскости.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Теорема: „Признак параллельности прямой и плоскости”.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.
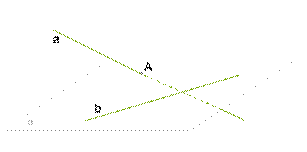
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит прямая a должна быть параллельна плоскости α
Перпендикуляр, наклонная, проекция наклонной.
Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
БИЛЕТ 6.
Скрещивающиеся прямые. Признак скрещивающихся прямых.
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
|
|
|
Признак скрещивающихся прямых: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB. 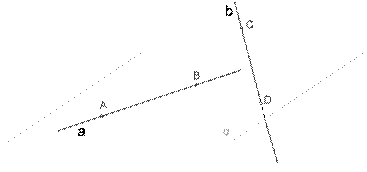
1. Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
2. Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.
Площадь боковой поверхности правильной пирамиды.
Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Апофема – высота боковой грани, опущенная из ее вершины.
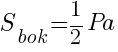
БИЛЕТ 7.
Теорема о существовании и единственности плоскости, проходящей через одну из скрещивающихся прямых и параллельной другой прямой.
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
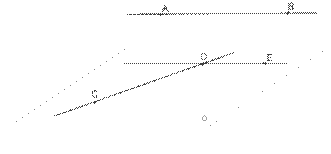
Рассмотрим скрещивающиеся прямые AB и CD.
|
|
|
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая AB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Аксиомы стереометрии.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
А4.Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей
А5.В пространстве существуют плоскости. В каждой плоскости выполняются все аксиомы планиметрии.
БИЛЕТ 8.
Дата добавления: 2018-06-01; просмотров: 1630; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
