Признак Параллельности двух прямых(теорема о параллельности трёх прямых).
БИЛЕТ 1.
Теорема о существовании и единственности плоскости, проходящей через прямую и точку не лежащей на ней.
Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Доказательство. Пусть АВ — данная прямая и С — не лежащая на ней точка (рис. 312). Проведем через точки А и С прямую (аксиома I). Прямые АВ и АС различны, так как точка С не лежит на прямой АВ. Проведем через прямые АВ и АС плоскость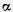 
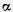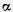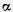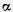(аксиома С3) Она проходит через прямую АВ и точку С. Докажем, что плоскость , проходящая через прямую АВ и точку С, единственна. Допустим, существует другая плоскость ', проходящая через прямую АВ и точку С. По аксиоме С2 плоскости и ' пересекаются по прямой. Эта прямая должна содержать точки А, В, С. Но они не лежат на одной прямой. Мы пришли к противоречию. Теорема доказана.
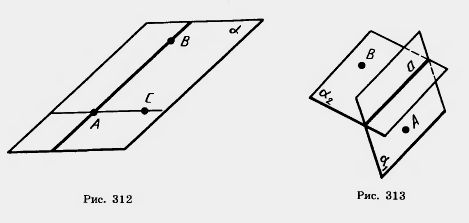
Параллелепипед. Виды параллелепипеда.
Параллелепипед — это четырёхугольная призма, все грани которой являются параллелограммами.
Виды параллелепипедов:
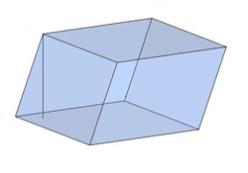Наклонный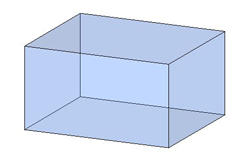 
Прямой
Виды прямых параллелепипедов:
Прямой параллелепипед, основание — параллелограмм
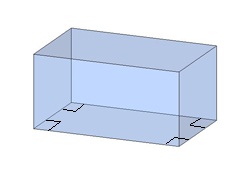
Прямоугольный параллелепипед, основание — прямоугольник
Специальные случаи прямоугольного параллелепипеда
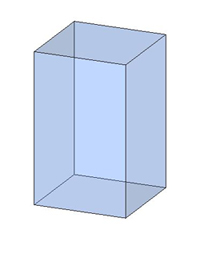
Правильная четырёхугольная призма, основание — квадрат, высота призмы не обязательно равна стороне основания
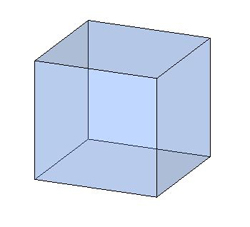
Куб, все рёбра куба равны, все грани — квадраты
|
|
|
БИЛЕТ 2.
Теорема о существовании и единственности плоскости, проходящей через две пересекающиеся прямые
Через две пересекающиеся прямые можно провести плоскость, притом только одну.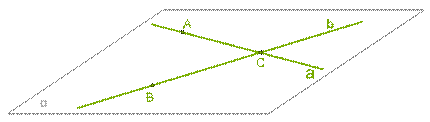 
Доказательство:
1) Рассмотрим прямые a и b, которые пересекаются в точке C.
2) Выберем точку A на прямой a и точку B на прямой b так, чтобы эти точки не совпадали с точкой C.
3) Из второй аксиомы следует, что через точки A, B и C можно провести одну единственную плоскостьα. В таком случае прямые a и b находятся на плоскостиα(судя по третьей аксиоме).
Тетраэдр. Сечения тетраэдра.
Правильный тетраэдр: частный случай правильной треугольной пирамиды.
Сечением многогранника плоскостью является многоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости, плоскость при этом называется секущей плоскостью.
БИЛЕТ 3.
Теорема о существовании и единственности прямой, параллельной данной и проходящей через точку, не лежащей на ней.
Через точку вне данной прямой можно провести прямую, параллельную данной и только одну.
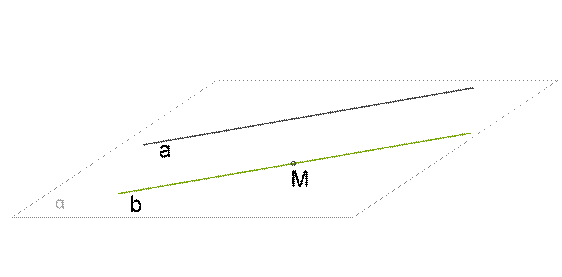
Доказательство:
1. Через данную прямую a и точку M, которая не лежит на прямой, проводится плоскость α.
|
|
|
2. Такая плоскость только одна (т.к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).
3. А в плоскости α через точку M можно провести только одну прямую b, которая параллельна прямой a.
Пирамида. Элементы. Виды.
N-угольная пирамида представляет собой многогранник, одна грань которого называется основанием пирамиды, - некоторый n-угольник, а остальные n граней- треугольники с общей вершиной. Эта общая вершина называется вершиной пирамиды, а треугольники - боковыми гранями пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами ее основания, называются боковыми ребрами пирамиды.
Виды:
Правильная
Треугольная
Тетраэдр
БИЛЕТ 4.
Признак Параллельности двух прямых(теорема о параллельности трёх прямых).
А)Две прямые a и b на плоскости, которые не пересекаются, называются параллельными и обозначаются a∥b.
Б) Две прямые, параллельные третьей прямой, параллельны.
Доказательство:
Выберем точку M на прямой b. Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
|
|
|
Возможны два случая: 1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α. Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L. Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек. Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
2)Свойства пирамиды у которой боковые ребра равны.
Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.
— все боковые ребра пирамиды образуют с плоскостью основания равные углы;
— все углы, которые боковые ребра образуют с высотой пирамиды, равны.
|
|
|
Билет 5.
Дата добавления: 2018-06-01; просмотров: 2102; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!