Наклонные асимптоты графика функции
Исследование функции с помощью производных: точки экстремума, выпуклость функции и точки перегиба. Асимптоты функции и их нахождение. Точками экстремума функции являются точки, в которых функция определена и проходя через которые производная меняет знак. Точки a,b называют точками строго экстремума или просто точками экстремума функции. То есть это обобщенный термин точек максимума и точек минимума. необходимым условием экстремума: Если в точкеx0есть экстремум, тоf '(x0) = 0либо значенияf '(x0)не существует. Условие необходимо, но не достаточно, и обратное утверждение справедливо далеко не всегда. Так, из равенства f '(x0) = 0 ещё не следует, что функция достигает максимума или минимума в точке x0. Классический пример– это кубическая парабола f(x) = x3 и её критическая точка x=0. Выпуклость/вогнутость графика характеризуетвторая производная функции. Пусть функция y=f(x) дважды дифференцируема на некотором интервале. Тогда: – если вторая производная f ‘’(x) < 0 на интервале, то график функции f(x) является выпуклым на данном интервале; – если вторая производная f ‘’(x) > 0 на интервале, то график функции f(x) является вогнутым на данном интервале. На счёт знаков второй производной по просторам учебных заведений гуляет доисторическая ассоциация: «–» показывает, что «в график функции нельзя налить воду» (выпуклость), а «+» – «даёт такую возможность» (вогнутость).
|
|
|
Необходимое условие перегиба
Если в точкеx0есть перегиб графика функции y=f(x), то:f ‘’(x0) = 0 либо значенияf ‘’(x0) не существует
Данная фраза подразумевает, что функция y=f(x) непрерывна в точке x0 и в случае f ‘’(x0) = 0 – дважды дифференцируема в некоторой её окрестности.
Необходимость условия говорит о том, что обратное справедливо не всегда. То есть из равенства f ‘’(x0) = 0 (либо небытия значения f ‘’(x0) ) ещё не следует существования перегиба графика функции y=f (x) в точке x0. Но и в той, и в другой ситуации x0 называюткритической точкой второй производной.
Достаточное условие перегиба
Если вторая производнаяy=f ‘’ (x) при переходе через точкуx0меняет знак, то в данной точке существует перегиб графика функцииy=f (x) .
Точек перегиба может не быть вовсе, и в этом смысле показательны некоторые элементарные образцы. Проанализируем вторую производную функции f (x)=x2: f ‘ (x)=2x ; f ‘'(x)=2
Получена положительная функция-константа, то есть для любого значения «икс» f ‘'(x)=2>0. Факты, лежащие на поверхности: парабола f (x)=x2 вогнута на всей области определения, точки перегиба отсутствуют. Легко заметить, что отрицательный коэффициент при x2 «переворачивает» параболу и делает её выпуклой (о чём нам сообщит вторая производная – отрицательная функция-константа).
|
|
|
Асимптота – это прямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные асимптоты, которые задаются уравнением вида x=α, где «альфа» – действительное число. Популярная представительница x=0 определяет саму ось ординат, вспоминаем гиперболу f(x)=1/x.
2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом y=kx+b. Иногда отдельной группой выделяют частный случай –горизонтальные асимптотыy=b. Например, та же гипербола с асимптотой y=0.
Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много.
Вертикальные асимптоты графика функции
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрывафункции. Всё просто: если в точке x=α функция y=f(x) терпит бесконечный разрыв, то прямая, заданная уравнением x=α является вертикальной асимптотой графика.
|
|
|
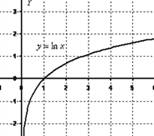
Таким образом, чтобы установить наличие вертикальной асимптоты x=α в точке x=α достаточно показать, что хотя бы один из односторонних пределов 
бесконечен (=+-бесконечности). Чаще всего это точка, где знаменатель функции равен нулю. Простейшая иллюстрация: f(x)=lnx и ось ординат
Из вышесказанного также следует очевидный факт: если функция непрерывна на 
, то вертикальные асимптоты отсутствуют. Например парабола.
Наклонные асимптоты графика функции
Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтомуграфик функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции f(x)=ex обладает единственной горизонтальной асимптотой при x→-∞, а график арктангенса f(x)=arctgx при x→-∞, x→+∞ – двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью x→+-∞. Например, …правильно догадались: 
.
Общее практическое правило:
Если существуют два конечных предела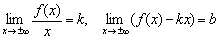 
, то прямая y=kx+b является наклонной асимптотой графика функции y=f(x) при x→+-∞. Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
|
|
|
Примечание: формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».
Дата добавления: 2018-06-27; просмотров: 880; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!