Рациональные алгебраические неравенства с параметрами
№6.x - |a| > 0. Решить неравенство для каждого значения параметра a.
 |
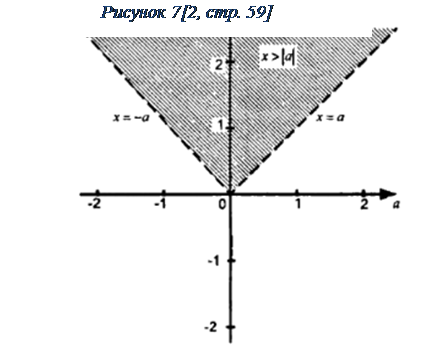Решение: На Рисунке 7на координатно-параметрической плоскости xOaизображено множествоточек (x, a), значения координаты и параметра каждой из которых которых удовлетворяют данному неравенству. Точки, расположенные выше графика функции x = |a|, являются элементами этого множества.
Каждому значению параметра a соответствуют точки изображенного множества с искомыми значениями координат.
Ответ: Если a< 0, то x> -a, если a = 0, то x> 0, если a> 0, тоx>a.
№7. Найти все значения параметра a, при которых неравенство
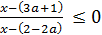выполняется для всех x из промежутка 2 ≤ x ≤ 3.
Решение:Решим неравенство F(x, a) =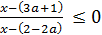
На координатно-параметрической плоскости на прямой x = 3a+1числитель обращается в нуль, а знаменатель на x = 2–2a. Эти прямые разбивают координатно-параметрическую плоскость на четыре “частичные области”.
 |
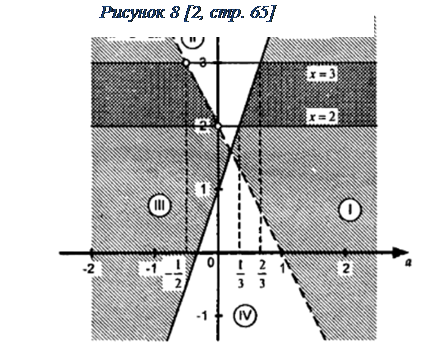Теперь нам предстоит определить знаки в каждой из областей, для этого необходимо взять любую точку из исследуемой области. Например, x=2, a=1F(2, 1) > 0. Следовательно, всюду в Iобласти F(x, a) > 0. В остальных областях определяем знаки по аналогии. Таким образом, получаем, что неравенство выполняется в Iи III областях, причем граница x=3a+1является его решением, а граница x=2-2a не принадлежит множеству решений рассматриваемого неравенства.
Пересечение данного множества с множеством точек, удовлетворяющих неравенству 2 ≤ x ≤ 3, дает решение данного неравенства на промежутке
|
|
|
2 ≤ x ≤ 3. Следовательно, данное неравенство выполняется сразу для всех x из промежутка 2 ≤ x ≤ 3 при a< -1/2и a ≥ 2/3.
Ответ: a< -1/2, a ≥ 2/3.
№8.Для каждого целочисленного значения параметра q найти целочисленные решения неравенстваx2-5(x-1)+3|x-q|-q ≤ 0.
Решение: Составим равносильную совокупность, состоящую из двух систем:
1) 
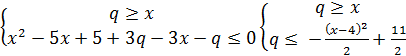
2) 
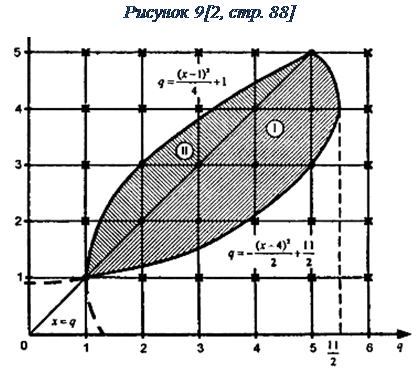
На координатно-параметрической плоскости xOq множество значений (x, q), удовлетворяющих полученной совокупности систем неравенств, ограничено двумя параболами. В вершинах парабол x=1, q=1 и x=4, q=11/2.
Покроем данное множество прямоугольной сеткой с целочисленными значениями координат xmи параметра qn: 1 ≤xm≤ 5, 1 ≤qn≤ 6.
Находим среди множества всех точек в узлах сетчатого прямоугольника те точки, которые принадлежат заштрихованному множеству, т.е. дают на координатно-параметрической плоскости целочисленные решения неравенства (на Рисунке9 эти точки изображены жирно, а точки, которые не дают решения – квадратами).
Ответ: Если q=1, то x=1;
если q=2, то x=2, x=3;
если q=3, то x=2, x=3;
если q=4, то x=3, x=4
если q=5, то x=3, x=4, x=5.
№9.Найти все значения a, при которых система неравенств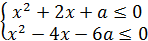 
имеет единственное решение.
|
|
|
Решение: На координатно-параметрической плоскости xOa решением данной системы неравенств является пересечение множеств I и II. Множество I состоит из всех точек плоскости, расположенных на параболе a = -x2 – 2x (1) и левее ее, а множество II–из точек, расположенных на параболе a = 1/6 ∙ (x2-4x) (2) и правее ее.
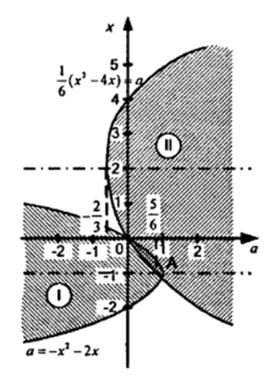
Рисунок 10[2, стр. 81]
Параболы (1) и (2) пересекаются в точках, для которых x = 0, a = 0 и x = -8/7 < -1 и a = 48/49 < 1.
В вершине A параболы (1) x = -1, a=1.
Точки O и A являются соответственно самой левой и самой правой точкой полученного множества решений системы неравенств.
Следовательно, при a< 0 и a> 1 данная система неравенств не имеет решений; при a = 0 и a = 1 – имеет единственное решение; при 0 <a< 1 – бесконечное множество решений.
Ответ: a = 0, a = 1.
Дата добавления: 2018-06-27; просмотров: 490; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!