Глава 2. Практическое применение координатно-параметрического метода в решении задач с параметром
Рациональные алгебраические уравнения с параметрами
№1.P(x, a) = x - |a| = 0. Решить уравнение для каждого значения параметра a.
 |
Решение: Для начала перенесем модуль в правую часть: x = |a|. Теперь воспользуемся определением модуля и запишем систему:
Разберем два случая:
1.График функции x = |a|, где параметр a – аргумент, изображен на Рисунке 1. График представляет собой множество всех точек (x, a) на координатно-параметрической плоскости xOa с горизонтальной параметрической осью Oa,значения координаты и параметра каждой из которых удовлетворяют полученной системе.
Точки координатно-параметрической плоскости xOa, значения координаты и параметра каждой из которых удовлетворяют выражению (I), расположены на части прямой x = a, находящейся в полуплоскости a ≥ 0с границей a = 0 (Рисунок 1 – заштрихованная часть).
Аналогично находим решение для выражения (II). Точки расположены на части прямой x = -a, находящейся в полуплоскости a< 0(Рисунок 1 – заштрихованная часть).
Таким образом, каждому значению параметраaсоответствует единственное значение координаты x.Если a< 0, то x = -a, если a = 0, то x = 0, если a> 0, то
x = a.
2.
 |
На Рисунке 2 изображено то же множество, но уже на координатно-параметрической плоскости aOx с вертикальной параметрической осью Oa. Каждая из прямых семейства a = const пересекает изображенное множество в точке с координатой x, которая определяет решение исходного уравнения. Если a = const< 0, то x = -a, если a = const = 0, то x = 0, если a = const> 0, то x = a. Таким образом, получаем такой же ответ, что и в первом случае.
|
|
|
Ответ: Еслиa< 0,тоx = -a, еслиa = 0, тоx = 0, еслиa> 0, тоx = a.
№2. Решить уравнение 2|x| + |x-1| = a.
Решение: применяем метод “частичных областей”. Получаем совокупность состояющую из трех систем:
I) 
II) 
III) 
На координатно-параметрической плоскости решением данного уравнения в I“частичной области”: х<0 (полуплоскости) является луч 
,во II области: 
(полосе)-отрезок прямой x=a-1,в III области: x>1(полуплоскости) - луч 
.
Используя решение на координатно-параметрической плоскости, можно записать ответ, поставив в соответствие каждому значению параметра а значение х на полученной ломаной линии.
Рисунок 3[2, стр.22]
Ответ:a<1: 
a>2 : 
№3.3|x+2a| - 3a + x – 15 = 0. При каких значениях параметра a все решения уравнения удовлетворяют неравенству 4 ≤ x ≤ 6?
Решение: Раскрываем модуль, получаем совокупность из двух систем:
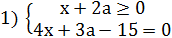
2) 
В данном номере прямая x + 2a = 0 разбивает координатно-параметрическую плоскость xOa на две “частичные области” 1) и 2).
Решением системы 1), удовлетворяющим условию 4 ≤ x ≤ 6, на координатно-параметрической плоскости является отрезок луча с началом в точке a = -3, x = 6 и концом a = 
, x = 4 (для нахождения a значения x подставляются в уравнение).
|
|
|
Аналогично находим решение для системы 2). Им является отрезок луча с началом в точке a = -3, x = 6 и a = 
,x = 4 (эти отрезки изображены на Рисунке 4 жирными линиями).
Оба решения удовлетворяют неравенству при всех значениях параметра a из отрезка [-3; ].
Ответ: -3 ≤ a ≤ .
№4.(2–x)(x+a) = 0. Найти все значения параметра a, при которых уравнение имеет два различных неотрицательных корня.
Решение: На координатно-параметрической плоскости xOa множество всех точек (x, a), значения координаты и параметра каждой из которых удовлетворяют данному уравнению, представляет собой параболу – график функции
a = (2-x)(x+1)
 |
Парабола пересекает ось Ox в точках x = -1, a = 0 и x = 2, a = 0. В вершине параболы x = 1/2, a = 9/4 оба корня совпадают. При 2 ≤a≤ 9/4 оба корня неотрицательны.
№5.Предприятие производит телевизоры и является прибыльным. Известно, что при изготовлении nтелевизоров в месяц расходы предприятия на выпуск одного телевизора составляют не менее 40500/n + 270 − |90−40500/n|тыс. руб., а цена реализации каждого телевизора при этом не превосходит 540- 3/10∙n тыс. руб. Определить ежемесячный объем производства, прикотором может быть получена наибольшая из возможных в данных условиях ежемесячная прибыль.
|
|
|
Решение: Пусть ежемесячная прибыль предприятия при изготовлении nтелевизоров – x (тыс. руб.). Тогда по условию задачи:
x ≤ (540n – 3/10 ∙ n)∙n – (40500/n +270 - |90 – 40500/n|) ∙n
x ≤ 540n – 3/10 ∙ n2 - 40500 – 270 + |90n - 40500|
x ≤ x(n) = 
 |
На координатно-параметрической плоскости xOn координата x – это кусочно-квадратичная функция действительного аргумента n, график которой состоит из частей двух парабол: x = x1(n) и x = x2(n). Так как x1’(n) = 0 =>n = 300и x2’(n) = 0 =>n = 600, то максимальное значение x = 27000 функции x = x1(n)и x = x2(n)достигают соответственно при n = 300и n = 600(по свойству кусочно-квадратичной функции).
Ответ: 300 или 600 телевизоров.
Дата добавления: 2018-06-27; просмотров: 529; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!