Классическое, статистическое и геометрическое определения вероятностей
Глава 1. Основные понятия теории вероятностей
Элементы комбинаторики
Комбинаторикой называется раздел математики, изучающий задачи выбора, расположения и упорядочения элементов из данного фиксированного множества М и методы подсчета числа всех возможных способов, которыми это можно сделать.
Основные правила комбинаторики
Рассмотрим фиксированное множество 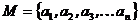 , содержащее п различных элементов.
, содержащее п различных элементов.
Правило суммы. Пусть элемент а1 из множества М можно выбрать числом n1 способов, элемент а2 из множества М можно выбрать числом n2 способов, элемент ак из множества М можно выбрать числом nk способов.
Тогда один из элементов множества М ( а1 , или а2, или, . . ., или ак ) можно выбрать числом п1+ п2 + . . . + пк способов.
Пример 1.1. Сколько существует способов приобрести кассовый аппарат, если в продаже есть 5 видов различных кассовых аппаратов производства Японии, 4 – производства США, 3 – производства Англии и 2 – производства Украины.
4Можно приобрести кассовый аппарат производства Японии - это можно сделать числом n1=5 способов, или производства США – это можно сделать числом n2=4 способов, или производства Англии – это можно сделать числом n3 = 3 способов, или производства Украины – это можно сделать числом n4 =2 способов. Всего способов приобретения кассового аппарата по правилу суммы будет n1+ n2 +n3+n4=5+4+3+2=14 способов. 3
Правило произведения. Пусть элемент а1 из множества М можно выбрать числом n1 способов, элемент а2. из множества М можно выбрать числом n2 способов, … элемент ак из множества М можно выбрать числом nk способов. Причем, выбор элемента а1 не влияет на число способов выбора всех последующих элементов, выбор элемента а2 не влияет на число способов выбора всех последующих элементов и т.д. Тогда все к элементов а1 ,а2, … , ак в указанном порядке можно выбрать числом n1 …nk способов.
Пример 1.2. В конкурсе на лучший проект экономического развития некоторой отрасли производства принимают участие 7 коллективов. Сколькими способами могут быть распределены между ними первое, второе и третье места?
4В конкурсе участвуют 7 коллективов, следовательно, первое место может быть распределено n1=7 способами, второе место ‑ n2 = 6, третье ‑ n3 = 5 способами. Тогда, по правилу произведения, число способов распределения призовых мест среди 7 коллективов: n1∙n2×n3=7 ×6 ×5=210.3
Формулы комбинаторики определяют число способов, которыми из множества М, содержащего n элементов, можно выбрать по определенным правилам какую-либо комбинацию k элементов, образующую подмножество Мk исходного множества.
Существуют две разные схемы выбора элементов: без повторений и с повторениями. В схеме выбора без повторений выбор элементов осуществляется без возвращения в исходное множество, т.е. выбранный элемент исключается из множества М и не участвует в дальнейшем выборе. При этом выбор может осуществляться как поэлементно, так и партиями. В схеме выбора с повторениями выбранный элемент фиксируется в подмножестве Мк и возвращается в исходное множество М. Таким образом, в выборе любого элемента подмножества Мk участвуют каждый раз все элементы множества М. Схема такого выбора осуществляется обязательно поэлементно.
Все выборки или подмножества элементов множества М называют соединениями. В соединениях можно учитывать или не учитывать порядок расположения элементов. В зависимости от этого их называют сочетания, размещения и перестановки .
Сочетаниями из n элементов по k называют произвольные неупорядоченные k-элементные подмножества Мk n-элементного множества М. Сочетания отличаются друг от друга только составом элементов. Порядок следования элементов в них не имеет значения.
Число сочетаний из n элементов по k обозначается 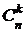 и вычисляется по формуле
и вычисляется по формуле
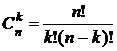 . (1.1)
. (1.1)
Символом n! (n факториал) обозначается произведение всех натуральных чисел от 1 до n, т.е. n!=1×2×3×…×n; k!=1×2×…×k; (n-k)!=1×2×…×(n-k). Принято считать 0!=1 и 1!=1 . Для числа сочетаний из п элементов по к имеют место соотношения:
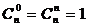 ;
; 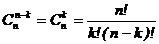 .
.
Пример 1.3. Предприятие выпускает 25 наименований продукции. Сколько существует способов выбрать 3 различных наименования продукции для презентации на выставке?
4Элементами множества М являются наименования продукции. Выбранные 3 наименования представляют неупорядоченное подмножество М3. Схема выбора - выбор без повторений. Тогда число способов выбора равно: 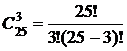 =
= 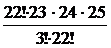 =
= 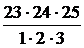 =
= 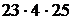 =2300.3
=2300.3
Размещениями из n элементов по k называют упорядоченные k-элементные подмножества Мk n-элементного множества М. Отличаются размещения друг от друга и составом элементов, и порядком их следования.
Число размещений из n элементов по kобозначается Ank и вычисляется по формуле
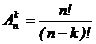 =n×(n-1)×(n-2)×…×(n-k+1) (1.2).
=n×(n-1)×(n-2)×…×(n-k+1) (1.2).
Пример 1.4. Сколько может быть составлено различных трехзначных кодов из десяти цифр от 0 до 9, если цифры в коде не повторяются?
4Код представляет собой упорядоченное 3-элементное подмножество, выбранное из 10-элементного множества М = {0, 1,…, 9}. Число возможных кодов, состоящих из различных цифр, равно
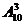 =
= 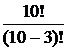 = =
= = 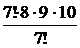 = 8×9×10 = 720.3
= 8×9×10 = 720.3
Перестановками называют размещения, в которых участвуют все элементы множества М.Если в перестановке изменить порядок следования элементов, то получится новая перестановка. Например, перестановками множества М={a,b,c} будут: М 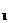 ={a,b,c}, М
={a,b,c}, М 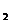 ={a,c,b}, М
={a,c,b}, М 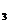 ={b,a,c}, М
={b,a,c}, М 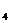 ={b,c,a}, М
={b,c,a}, М 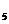 ={c,a,b}, М
={c,a,b}, М 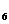 ={c,b,a}.
={c,b,a}.
Число всех перестановок п-элементного множества обозначается Pn и вычисляется по формуле:
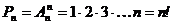 (1.3)
(1.3)
Это число определяет, сколькими способами можно упорядочить множество, состоящее из nэлементов.
Пример 1.5. К билетной кассе одновременно подошли 5 человек. Сколько существует способов составить из них очередь?
4Очередь - это упорядоченное множество, число способов составить очередь равно: P5 = 5! = 1×2×3×4×5 = 120.3
Сочетаниями с повторением из n элементов по k называют k-элементные неупорядоченные подмножества Мk, в которых элементы могут повторяться.
Число сочетаний из n элементов по k с повторением обозначается fnk и вычисляется по формуле:
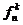 =
= 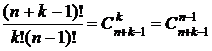 . (1.4)
. (1.4)
Пример1.6.Каждая кость домино представляет собой комбинацию из двух чисел от 0 до 6. Сколько различных костей содержит игра?
4Каждая кость домино состоит из двух полей, точки на поле определяют число, следовательно, кость можно рассматривать как неупорядоченное 2-элементное подмножество М2, элементы которого выбраны из 7 элементов множества М = {0,1,2,3,4,5,6}. Поля на кости могут определяться и одинаковыми числами, т.е. элементы М2 могут повторяться. Тогда число различных костей в игре равно:
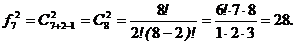 3
3
Размещениями с повторением изn элементов по k называют упорядоченное k-элементное подмножество Мkу, элементы которого могут повторяться. К размещениям с повторением приводит схема выбора с повторением.
Число размещений из n элементов по k с повторениемобозначается Ank(повт) и вычисляется по формуле
Ank(повт) = 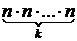 =nk. ( 1.5 )
=nk. ( 1.5 )
Пример 1.7. Сколько может быть составлено различных трехзначных кодов из десяти цифр от 0 до 9, если цифры в коде могут повторяться?
4Код описывается упорядоченным 3 элементным подмножеством с повторяющимися элементами, составленным из множества М={0,1,…,9}. Число кодов равно: 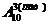 =103=1000.3
=103=1000.3
Перестановками с повторением называют различные упорядоченные множества, состоящие из одних и тех же, но отличающихся расположением элементов, причем некоторые элементы множества одинаковы. Например, перестановками множества М={a,а,c,b} будут: М1={a,а,c,b}, М2={a,c,а,b}, М3={с,a,а,b}, М4={b,c,a,a}, М5={a,b,c,a}, М6={a,a,b,c}, М7={a,b,а,c}, М8={b,a,а,c}, М9={c,b,a,a}, М10={a,c,b,a}, М11={b,а,c,a}, М12={c,a,b,а}.
Пусть задано n-элементное множество М, которое содержит k1 элементов первого типа, k2 элементов второго типа, …, km элементов m-го типа, причем k1+k2+…+km=n. Число перестановок n-элементного множества с повторением обозначается Pn(k1,k2,…,km) и вычисляется по формуле:
Pn(k1,k2,…,km)= 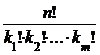 . (1.6)
. (1.6)
Пример 1.8. Предприятие для маркировки своей продукции использует товарный знак, состоящий из 4 полос, две из которых красного цвета, одна- желтого и одна – синего. Сколько различных товарных знаков может быть составлено с такой маркировкой?
4Товарный знак – это упорядоченное множество, состоящее из 4 элементов, среди которых два повторяются, т.е. имеем n=4, k1=2, k2=1, k3=1. Число N различных товарных знаков будет:
N=P4(2,1,1)= 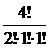 =12.3
=12.3
Разбиение множества на группы. Разбиением множества на группы называют представление n элементного множества М в виде суммы m попарно непересекающихся подмножеств 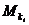 , (i=
, (i= 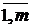 ), содержащих соответственно ki элементов, причем k1+k2+…+km = n. Число способов, которыми М можно разбить на группы
), содержащих соответственно ki элементов, причем k1+k2+…+km = n. Число способов, которыми М можно разбить на группы 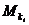 , обозначается Cn (k1,k2,…,km) и вычисляется по формуле:
, обозначается Cn (k1,k2,…,km) и вычисляется по формуле:
Cn(k1,k2,…,km) = 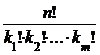 . (1.7)
. (1.7)
Пример 1.9. Сколькими способами можно расселить в общежитии 8 студентов по 3 комнатам: одноместной, трехместной и четырехместной?
4Здесь n =8, k1=1, k2=3, k3=4. Число способов расселения равно:
C8(1,3,4) = 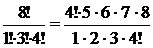 =5×7×8= 280.3
=5×7×8= 280.3
Задачи
1.1. Сколько существует способов провести воскресный вечер, если выбирать между посещением театра, дискотеки, ресторана, кинотеатра, считая, что территориально удобно расположены 5 театров, 4 дискотеки, 6 ресторанов и 3 кинотеатра?
Ответ: 18.
1.2. Имеется 5 видов конвертов без марок и 4 вида марок одинаковой стоимости. Сколькими способами можно выбрать конверт с маркой для посылки письма?
Ответ: 20.
1.3. У одного студента 5 книг, у другого – 9. Все книги различные. Сколькими способами студенты могут произвести обмен: а) одной книги на одну? б) двух книг на две книги?
Ответ: а) 45; б) 360.
1.4. На вершину горы ведут 5 тропинок. Сколькими способами турист может подняться в гору и потом спуститься с нее, если а) подъем и спуск могут происходить и по одной тропинке; б) подъем и спуск должны происходить по разным тропинкам?
Ответ: а) 25; б) 20.
1.5. На окружности выбрано 10 точек. а) Сколько можно провести хорд с концами в этих точках? б) Сколько существует треугольников с вершинами в этих точках?
Ответ: а) 45; б) 120.
1.6. Сколькими способами можно выбрать три различные краски из имеющихся пяти?
Ответ: 10.
1.7. Сколько различных трехцветных полосатых флагов можно сшить, если имеется материал пяти различных цветов?
Ответ: 60.
1.8. Сколько словарей надо издать, чтобы можно было непосредственно выполнить переводы с любого из 5 языков: украинского, русского, английского, немецкого и французского – на любой другой из этих 5 языков?
Ответ: 20.
1.9. Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?
Ответ: 210.
1.10. Сколькими способами можно поставить на библиотечной полке 3 экземпляра учебника по высшей математике, 2 экземпляра учебника по теории вероятностей и один экземпляр учебника по информатике?
Ответ: 60.
1.11. В команду КВН отбирают 5 игроков из 10 претендентов. Сколькими способами это можно сделать, если два определенных претендента должны обязательно войти в команду?
Ответ: 56.
1.12. В течение четырех недель студенты сдают пять экзаменов, в том числе экзамен по теории вероятностей и по информатике. Сколькими способами можно распределить экзамены по неделям так, чтобы экзамены по теории вероятностей и по информатике не следовали друг за другом?
Ответ: 12.
1.13. Сколько существует способов рассадить 6 посетителей кафе: а) за круглый стол; б) за стойку бара.
Ответ: а) 5!=120; б) 6!=720.
1.14. Имеется 5 сигнальных фишек различной расцветки для маркировки товаров. Сколько видов товара можно промаркировать, если для маркировки использовать а) 2 фишки из 5; б) 3 фишки из 5; в) 4 фишки из 5; г) различное количество фишек.
Ответ: а) 20; б) 60; в) 120; г) 320.
1.15. Для маркировки товара имеются сигнальные фишки трех различных цветов, количество фишек каждого цвета не ограничено. Маркировки могут состоять из одной, двух или трех фишек, причем цвет фишек в маркировке может быть и одинаков. Сколько различных маркировок можно составить из имеющихся фишек?
Ответ: 39.
1.16. Три фининспектора проверяют 6 фирм. Сколькими способами это можно сделать, если проверку одной фирмы производит один инспектор, и каждый инспектор может проверить только две фирмы?
Ответ: 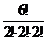 = 90.
= 90.
1.17. Сколько букв русского алфавита может быть передано азбукой Морзе, состоящей из точек и тире, если для передачи одной буквы отводить а) ровно 4 позиции; б) не более 4 позиций; в) равно 5 позиций.
Ответ: а) 16; б) 30; в) 32.
1.18. Номер автомобиля состоит из 2-букв латинского алфавита и трехзначного числа. Сколько существует автомобильных номеров?
Ответ: 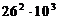 =676000.
=676000.
1.19. В учебной группе 25 студентов. Сколько существует способов разбить группу на 3 подгруппы по 7, 8, и 10 человек для проведения лабораторных занятий?
Ответ: 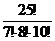 .
.
1.20. Восемь человек должны сесть в 2 автомобиля, причем в каждом должно быть не менее 3 человек. Сколькими способами они могут это сделать?
Ответ: 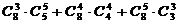 =126.
=126.
1.21. В соревнованиях на первенство страны по футболу принимают участие 12 команд. Сколькими способами могут быть распределены между командами золотая, серебряная и бронзовая медали?
Ответ: 1320.
1.22. Сколько различных шестизначных шифров можно получить, из цифр 1,2,3,4,5,6,7,8,9, если каждый шифр должен состоять из 3 четных и 3 нечетных цифр, причем никакая цифра не входит в шифр более одного раза?
Ответ: 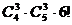 =28 800.
=28 800.
1.23. Фирма закупила четыре различные партии товара. Сколькими способами можно распределить эти партии среди 12 фирменных магазинов, так, чтобы ни один магазин не получил более одной партии нового товара?
Ответ: 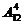 =11880.
=11880.
1.24. Сколькими способами можно расставить на витрине 9 различных экспонатов так, чтобы рядом стоящими оказались: а) два; б) три; в) четыре определенных экспоната?
Ответ: а) 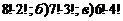 .
.
1.25. Сколько существует вариантов опроса 11 студентов на одном занятии, если ни один из них не будет опрошен дважды и на занятии может быть опрошено любое количество студентов, причем порядок опроса безразличен?
Ответ: 2047. (Воспользоваться свойством сочетаний: 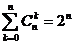 ).
).
1.26. Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй – не более десяти человек?
Ответ:1573.
1.27. Сколькими способами 3 различного вида работ Т1, Т2, Т3 можно распределить между 15 исполнителями, если а) никто из исполнителей не должен выполнять более одной работы; б) работу Т1 должно получить определенное лицо?
Ответ: а) 2730; б) 182.
1.28. В пригородном электропоезде 9 вагонов. Сколькими способами можно распределить для проверки бригаду из 4 контролеров, если все контролеры должны начать проверку одновременно и в различных вагонах?
Ответ: 3024.
1.29. В бригаде 9 человек. Сколько можно образовать разных звеньев из состава бригады при условии, что в звено входит не менее двух рабочих.
Ответ: 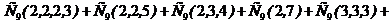
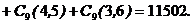
1.30. Сколько существует различных идентификационных кодов, состоящих из пяти цифр, если первая цифра не равна нулю?
Ответ: 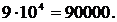
1.31. Менеджеру из своего офиса нужно попасть на деловую встречу, посетив при этом предприятие N, затем вернуться в офис, предварительно опять побывав в N. Сколькими способами он может это сделать, если из офиса в N можно попасть тремя путями, а из N в фирму ведут 4 пути?
Ответ: 144.
1.32. Сколькими способами можно расставить на стоянке 7 различных автомобилей в один ряд, если: два определенных автомобиля а) должны стоять рядом; б) не должны стоять рядом? Ответ: а) 2∙ 6!; б) 5∙6!.
1.33. Сколькими способами можно выбрать четырехзначное число, в десятичной записи которого нет нуля?
Ответ: 6561.
1.34. Сколько различных буквосочетаний можно получить из всех букв слова "экономика"?
Ответ: 9!/(2! ∙2!).
1.35. Сколько различных 10 позиционных кодов можно составить из шести вертикальных и четырех горизонтальных штрихов, если на одну позицию помещать только один штрих?
Ответ:210.
1.36. Найти число всевозможных буквосочетаний из букв слова: а)"сессия", б)"программирование".
Ответ: а) 6!/3!; б)16!/(3!∙2!∙2!∙2!∙2!);
А сколько таких буквосочетаний, в которых 3 буквы а) "с", б) "р" стоят рядом?
Ответ: а) 4!; б) 14!/(2! ∙2! ∙2! ∙2!).
1.37. Имеется 20 наименований товаров. Сколькими способами их можно распределить по 3 магазинам, если известно, что в первый магазин должно быть доставлено 8 наименований, во второй – 7 наименований и в третий – 5 наименований товаров?
Ответ:20!/(8!∙7!∙5!).
1.38. Сколькими способами можно распределить 9 программистов для работы в трех фирмах, если в первую должно быть распределено два, во вторую – три и в третью - четыре программиста?
Ответ: 1260.
1.39. Абитуриент должен сдать четыре вступительных экзамена. Он полагает, что для поступления достаточно набрать 17 баллов. Сколькими способами он может сдать экзамены, набрав не менее 17 баллов и не получив ни одной двойки?
Ответ: 31.
1.40. В кошельке лежат по две монеты достоинством в 1, 2, 5, 10 копеек и по одной монете в 25 и 50 копеек. Сколькими способами можно уплатить этими монетами за покупку стоимостью 76 копеек?
Ответ:4.
Случайные события
Теория вероятностей изучает закономерности массовых, случайных явлений. Одним из основных понятий теории вероятностей является понятие случайного события.
Событием называется всякий факт, который в результате опыта (испытания) может произойти или не произойти.
Примеры событий: получение прибыли при заключении сделки, отказ технического устройства за время его работы, искажение информации при передаче сообщения, получение качественного или бракованного изделия при его изготовлении.
Достоверным называется событие, которое при испытании обязательно произойдет. Обозначают достоверное событие латинской буквой U.
Невозможным называется событие, которое при испытании заведомо не произойдет. Это событие обозначают буквой V.
Случайным называется событие, которое при испытании может произойти или не произойти. Обозначаются случайные события большими буквами латинского алфавита: A, B, C, . . . .
Равновозможными называются случайные события, которые могут произойти с одинаковой возможностью.
Два события называют совместными, если появление одного из них не исключает появления другого. Если появление одного события исключает появление другого, то события несовместны.
Несколько событий называются А1, А2,…, Аn называют попарно несовместными, если появление каждого из них исключает появление любого из остальных.
События А1, А2,…, Аn образуют полную группу событий, если они попарно несовместны, и в результате опыта одно из них обязательно произойдет.
Операции над событиями
Операции над событиями определяют правила действий с событиями и позволяют выражать одни события через другие.
 Суммой (объединением) событий А и В называется событие С=А+В (С=АÈВ), состоящее в том, что произойдет хотя бы одно из них ( или А, или В, или оба) . На диаграмме (рис 1.2.) событию С соответствует заштрихованная область С, представляющая объединение областей А и В. Аналогично, суммой нескольких событий А1, А2,…, Аn называется событие С, состоящее в том, что произойдет хотя бы одно из событий Аi, i=
Суммой (объединением) событий А и В называется событие С=А+В (С=АÈВ), состоящее в том, что произойдет хотя бы одно из них ( или А, или В, или оба) . На диаграмме (рис 1.2.) событию С соответствует заштрихованная область С, представляющая объединение областей А и В. Аналогично, суммой нескольких событий А1, А2,…, Аn называется событие С, состоящее в том, что произойдет хотя бы одно из событий Аi, i= 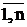 . Если события А1, А2,…, Аn образуют полную группу, то их сумма равна достоверному событию:
. Если события А1, А2,…, Аn образуют полную группу, то их сумма равна достоверному событию: 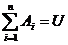 .
.
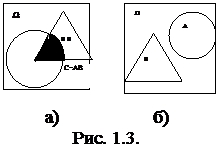 Произведением (пересечением) событий А и В называется событие С=А×В (С=АÇВ), состоящее в совместном появлении событий А и В. На рис 1.3.а событие С представлено пересечением областей А и В. Если А и В – несовместные события, то их произведение - невозможное событие , т. е. А×В=V (рис. 1.3.б).
Произведением (пересечением) событий А и В называется событие С=А×В (С=АÇВ), состоящее в совместном появлении событий А и В. На рис 1.3.а событие С представлено пересечением областей А и В. Если А и В – несовместные события, то их произведение - невозможное событие , т. е. А×В=V (рис. 1.3.б).
Произведение событий А1, А2,…, Аn – это событие С, состоящее в совместном появлении всех событий Аi, i= 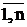 : С=
: С= 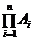 . Произведения попарно несовместных событий А1, А2,…, Аn – невозможные события: Аi×Аj=V, для любого i¹j.
. Произведения попарно несовместных событий А1, А2,…, Аn – невозможные события: Аi×Аj=V, для любого i¹j.
 Противоположным событием
Противоположным событием 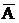 для события А называется событие, состоящее в том, что событие А не произошло.
для события А называется событие, состоящее в том, что событие А не произошло.
Свойства операций над событиями.
1. Переместительные свойства: А+В=В+А, А·В=В·А.
2. Сочетательные свойства: (А+В)+С=А+(В+С), (АВ)С=А(ВС).
3. Распределительное свойство: А(В+С)=АВ+АС.
4. Из определений операций над событиями следуют свойства:
А+А=А; А+U=U; А+V=А; А·А=А; А·U=А; А·V=V.
5 . Из определения противоположного события следует, что:
А+ 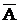 =U; А×
=U; А× 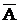 =V;
=V; 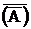 =А;
=А; 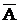 =V;
=V; 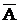 =U; U+V=U; U×V=V.
=U; U+V=U; U×V=V.
Классическое, статистическое и геометрическое определения вероятностей
Вероятность - это количественная мера возможности появления случайного события А и обозначается она Р(А).
Классическое определение вероятности.События, составляющие при данном испытании полную группу попарно несовместных, равновозможных событий, называют элементарными случаями. Те из элементарных случаев, при которых наступает событие А, называют благоприятствующими событию А.
Вероятностью события А называют отношение числа благоприятствующих элементарных случаев к общему числу всех элементарных случаев. Вероятность определяется формулой
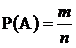 , (1.7)
, (1.7)
где m – число элементарных случаев, благоприятствующих событию А,
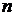 ‑ число всех возможных элементарных случаев.
‑ число всех возможных элементарных случаев.
Пусть проводится опыт, в результате которого могут наступить те или иные события. Если эти события образуют полную группу попарно несовместных и равновозможных событий, то говорят, что опыт обладает симметрией возможных исходов и сводится к "схеме случаев". Для опытов, которые сводятся к схеме случаев, применима классическая формула вероятности.
Пример 1.13. В лотерее разыгрывается 1000 билетов, среди которых 5 выигрышных. Определить вероятность того, что при покупке одного билета будет получен выигрыш.
4Элементарным событием этого опыта является покупка билета. Каждый билет лотереи неповторим, так как имеет свой номер, и купленный билет не возвращается обратно. Событие А заключается в том, что куплен выигрышный билет. При покупке одного из 1000 билетов всевозможных исходов опыта будет 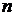 =1000, исходы образуют полную группу несовместных событий. Число исходов, благоприятных событию А, равно
=1000, исходы образуют полную группу несовместных событий. Число исходов, благоприятных событию А, равно 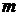 =5. Вероятность получить выигрыш, купив один билет, равна Р(А) =
=5. Вероятность получить выигрыш, купив один билет, равна Р(А) = 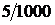 = 0.005.3
= 0.005.3
Для непосредственного подсчета вероятностей удобно применять формулы комбинаторики. Рассмотрим это на примере задачи выборочного контроля.
Пример 1.14. Пусть имеется партия из 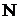 изделий, среди них есть
изделий, среди них есть 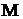 бракованных. Для контроля отбирается часть из
бракованных. Для контроля отбирается часть из 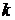 изделий. Какова вероятность того, что среди отобранных изделий будет ровно
изделий. Какова вероятность того, что среди отобранных изделий будет ровно 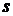 бракованных?
бракованных?
4 Число всех элементарных случаев 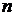 – это число способов, которыми можно отобрать
– это число способов, которыми можно отобрать 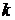 изделий из партии содержащей
изделий из партии содержащей 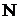 изделий, оно равно числу сочетаний из
изделий, оно равно числу сочетаний из 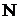 элементов по
элементов по 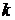 :
: 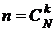 . Число элементарных случаев, благоприятствующих событию А согласно правилу умножения комбинаторики, будет
. Число элементарных случаев, благоприятствующих событию А согласно правилу умножения комбинаторики, будет 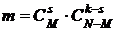 . Тогда искомая вероятность
. Тогда искомая вероятность 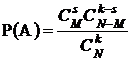 .
.
Например, пусть 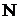 =100,
=100, 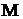 =10,
=10, 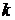 =10,
=10, 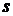 =1. Тогда вероятность того, что среди отобранных 10 изделий будет ровно одно бракованное, равна
=1. Тогда вероятность того, что среди отобранных 10 изделий будет ровно одно бракованное, равна
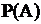 =
= 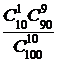 =
= 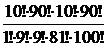 =
= 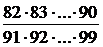 » 0.408. 3
» 0.408. 3
Классическое определение вероятностей применимо только в тех случаях, когда испытания обладают симметрией, можно выделить равновозможные элементарные случаи и число их конечно. Для большинства реальных задач эти требования практически невыполнимы и на ряду с классическим пользуются другими определениями вероятностей.
Статистическое определение вероятности. Пусть эксперимент заключается в проведении серии п испытаний, повторяющих один и тот же опыт, исходом которого может быть появление или не появление события А. И пусть во всей этой серии событие А наступило ровно 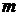 раз.
раз.
Относительной частотой W(A) появления события А называют отношение числа m опытов, в которых событие А наступило, к общему числу п всех проведенных опытов:
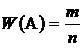 . (1.8)
. (1.8)
Относительная частота обладает свойством устойчивости: если число опытов в серии достаточно велико, то относительные частоты события А в различных сериях одного и того же эксперимента мало отличаются друг от друга.
Статистической вероятностью события называют число, к которому стремятся относительные частоты, если число опытов неограниченно возрастает:
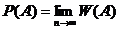 . (1.9)
. (1.9)
Пример 1.15. Метеорологические наблюдения в течении 10 лет в некоторой местности показали, что число дождливых дней в июле было в разные года равно: 2; 4; 3; 2; 4; 3; 2; 3; 5; 3. Определить вероятность того, что какой-либо определенный день июля будет дождливым.
4Событие А заключается в том, что определенный день июля, например, 10 июля, пойдет дождь. Выданная статистика не содержит информации о том, в какие конкретно дни июля шел дождь, поэтому можно считать, что все дни равновозможные для этого события. Один год – это одна серия испытаний из 31 одного дня. Всего серий 10. Относительные частоты серий равны: 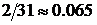 ,
, 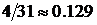 ,
, 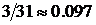 ,
, 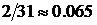 ,
, 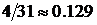 ,
, 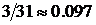 ,
, 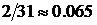 ,
, 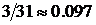 ,
, 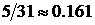 ,
, 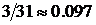 . Частоты различны, но наблюдается их колебание вокруг числа 0.1. Это число и можно принять за вероятность события А. Если за одну серию испытаний принять все дни июля за десять лет, то статистическая вероятность события А будет равна
. Частоты различны, но наблюдается их колебание вокруг числа 0.1. Это число и можно принять за вероятность события А. Если за одну серию испытаний принять все дни июля за десять лет, то статистическая вероятность события А будет равна
W(A)= 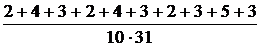 =
= 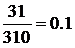 .3
.3
Геометрическое определение вероятности. Это определение вероятности обобщает классическое определение на случай, когда число элементарных случаев бесконечно.
Геометрической вероятностью события А называется отношение меры 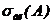 области, благоприятствующей появлению события, к мере
области, благоприятствующей появлению события, к мере 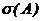 всей области:
всей области: 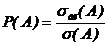 (1.10)
(1.10)
Если области представляют собой а) длины отрезков 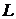 , б) площади фигур
, б) площади фигур 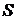 , в) объемы пространственных фигур
, в) объемы пространственных фигур 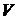 , то геометрические вероятности соответственно равны:
, то геометрические вероятности соответственно равны:
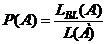 ;
; 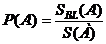 ;
; 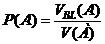 . (1.11)
. (1.11)
Пример 1.16. Рекламные объявления развешены с интервалом в 10 метров вдоль торгового ряда. Широта обзора у некоторого покупателя составляет 3 метра. Какова вероятность того, что он не заметит рекламу, если он движется перпендикулярно торговому ряду и пересечь ряд может в любой точке?
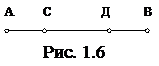 4Участок торгового ряда, расположенный между двумя объявлениями, можно представить как отрезок прямой АВ (рис. 1.6).Чтобы покупатель заметил объявления, он должен пройти через отрезки АС или ДВ, равные 3м. Если же он пересечет торговый ряд в одной из точек отрезка СД, длина которого 4м, то он не заметит рекламы. Вероятность этого события будет Р =
4Участок торгового ряда, расположенный между двумя объявлениями, можно представить как отрезок прямой АВ (рис. 1.6).Чтобы покупатель заметил объявления, он должен пройти через отрезки АС или ДВ, равные 3м. Если же он пересечет торговый ряд в одной из точек отрезка СД, длина которого 4м, то он не заметит рекламы. Вероятность этого события будет Р = 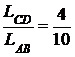 =0.4. 3
=0.4. 3
Задачи
1.41. Лотерея выпущена на общую сумму n гривен. Цена одного билета r гривен. Ценные выигрыши падают на m билетов. Определить вероятность выигрыша на один билет.
Ответ: ( mr)/n.
1.42. 1 сентября на одном из учебных потоков экономического факультета по расписанию должно быть три занятия по разным предметам. Всего на потоке в этом семестре изучается 10 предметов. Студент, не успевший ознакомиться с расписанием, пытается его угадать. Какова вероятность успеха этого опыта, если считать, что любое расписание из трех предметов равновероятно?
Ответ: 1/720.
1.43. На складе торговой фирмы находятся однотипные товары, изготовленные разными фирмами; из них: а товаров изготовлены фирмой "АВС", b товаров – фирмой "F&N", с товаров – фирмой "ЭХО". При ревизии на складе просматривают один за другим все имеющиеся товары и отмечают места их изготовления. Найти вероятность того, что при этом: а) первым появится товар фирмы "F&N"; б) из m просмотренных товаров k (k£c) будут фирмы "ЭХО"; в) из m просмотренных товаров все m (m£b) будут фирмы "АВС".
Ответ: а) b/(a+b+c); б ) 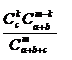 ; в)
; в) 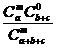 .
.
1.44. На книжной полке в случайном порядке расставлено 20книг, среди них двухтомник Л.Н. Толстого "Война и мир". Предполагая, что различные расположения книг равновероятны, найти вероятность того, что оба тома будут расположены рядом.
Ответ . 0,1.
1.45. На круглой вращающейся полке расставлено 10 видеокассет, среди них два видеофильма с Р. Гиром в главной роли. Предполагая, что различные расположения кассет равновероятны, найти вероятность того, что оба фильма с Р. Гиром будут стоять рядом.
Ответ: 2/9 .
1.46. В коробке лежит 20 канцелярских кнопок, из них 5 – бракованных. Наугад взяли 10 кнопок. Найти вероятность того, что среди них: а) нет бракованных; б) ровно одна бракованная; в) ровно две бракованные.
Ответ: а) 0,0162; б) 0,135; в) 0,348.
1.47. Найти вероятность того, что дни рождения 12 человек придутся на различные месяцы года.
Ответ: 12!/ 12 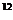 .
.
1.48. Из колоды в 36 карт вынуты три карты. Какова вероятность того, что: 1) две из них бубновой масти; 2) две из них одной масти; 3) хотя бы одна из них бубновой масти; 4) хотя бы одна из них ‑ туз?
Ответ: а) 0,136; б) 0,545; в) 0,5903; г) 0,305.
1.49. В урне имеются 10 шаров: 3 белых, 2 красных и 5 черных. Из урны наугад вынимается один шар. Найти вероятность того, что этот шар: а) белый; б) черный; в) не белый, г) белый или красный; д) не черный.
Ответ: а) 0,3; б) 0,5; в) 0,7; г) 0,5; д) 0,5.
1.50. Брошены три монеты. Найти вероятность, что выпадут а) два герба; б) три герба; в) герб не выпадет.
Ответ: а) 3/8; б) 1/8; в) 1/8.
1.51. Игральная кость бросается один раз. Какова вероятность того, что выпадет: а) четное число очков; б) 4 очка; в) не более 3 очков.
Ответ: а) 0,5; б) 1/6. в) 1/2.
1.52. В урне 3 белых и 7 черных шаров. Наудачу извлекли 2 шара. Какова вероятность того, что они будут разного цвета?
Ответ: 7/15.
1.53. Какова вероятность того, что в выбранном наугад трехзначном номере две цифры одинаковые, а третья отличается от них?
Ответ: 0,27.
1.54. Полная колода карт (52 карты) делится случайным образом на две равные части. Найти вероятности того, что: а) в каждой части окажется по два туза; б) в одной из частей не будет ни одного туза; в) в одной из частей будет ровно один туз.
Ответ: 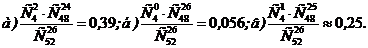
1.55. Карточка лотереи содержит 49 номеров. Для участия в лотерее необходимо купить карточку, отметить в ней 6 номеров и карточку сдать. При розыгрыше тиража лотереи определяется 6 выигравших номеров из 49. Найти вероятности событий: Аi={верно угаданы i выигрышных номера из 6}, если i =3,4,5,6.
Ответ: 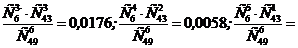
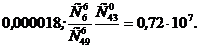
1.56. В картотеке 20 перенумерованных карточек. Наугад вынимают одну за другой и номера записывают. Какова вероятность того, что номера будут идти: а) в естественном порядке: 1,2,…,20; б) в обратном порядке: 20,19,…,1.
Ответ: а) 1/20!; б) 1/20!.
1.57. Решить предыдущую задачу при условии, что каждая карточка после вынимания и записи номера кладется обратно и перемешивается с остальными.
Ответ: 1/20 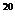 .
.
1.58. В розыгрыше первенства по баскетболу участвуют 18 команд, из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований имеется 5 команд экстракласса. Найти вероятность того, что: а) все команды экстракласса попадут в одну группу; б) две команды экстракласса попадут в одну группу, а три – в другую.
Ответ: а) 1/68; б) 6/17.
1.59. Окрашенный куб распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь: а) одну; б) две; в) три; г) ни одной окрашенной грани.
Ответ: а) 0,384; б) 0,096; в) 0,008; г) 0,512.
1.60. Какова вероятность соединиться с нужным абонентом, набрав наугад шестизначный телефонный номер, состоящий из различных цифр? Как изменится эта вероятность, если а) наугад набраны только три забытые цифры; б) если цифры номера могут повторяться?
Ответ: 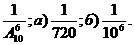
1.61. Из четырех букв разрезной азбуки составлено слово "соль". Ребенок, не умеющий читать, рассыпал эти буквы и собрал в произвольном порядке. Найти вероятность того, что у него получится слово "лось".
Ответ: 1/24..
1.62. В условиях предыдущей задачи, какова вероятность того, что из рассыпавшегося слова "колокол" будет составлено опять слово "колокол"?
Ответ: 1/210.
1.63. Ребенок, играя шестью карточками, на которых написаны буквы: М,Л,К,О,О,О, сложил слово "МОЛОКО". Какова вероятность того, что он не умеет читать? Какой будет вероятность этого события, если ребенок играет десятью карточками с буквами: М,М,Т,Т,А,А,А,К,И,Е, и складывает слово "МАТЕМАТИКА"?
Ответ: 1/120; 2!2!3!/10!=24/10!.
1.64. В кондитерской имеется 7 видов пирожных. Покупатель выбил чек на 4 пирожных. Считая, что любой набор пирожных равновероятен, вычислить вероятность того, что покупатель заказал: а) пирожные одного вида; б) пирожные разных видов; в) по два пирожных различных видов.
Ответ: 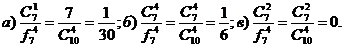
1.65. Для участия в телепередачи об университете необходимо выбрать 5 студентов. Студенты выбираются случайным образом из победителей студенческих олимпиад, которых в университете 15 человек, среди них 4 – студенты первого и второго курсов, 6 третьекурсников и 5 старшекурсников. Найти вероятности того, что: а) будут выбраны одни третьекурсники; б) все первокурсники и второкурсники будут участвовать в передаче; в) в передаче будут участвовать только старшекурсники; г) ни один третьекурсник не попадет на передачу; д) будут выбраны: два студента младших курсов, один студент третьего курса, 2 студента старших курсов.
Ответ: а) 0,002; б) 0,0036; в) 0,0003; г) 0,042; д) 0,12.
1.66. Какова вероятность того, что в группе из 30 студентов у двоих дни рождения совпадут?
Ответ: 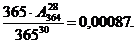
1.67. В доме 7 этажей. На первом в лифт входят 3 человека. Каждый из них с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Найти вероятность того, что 1) все выйдут на четвертом этаже; 2) все выйдут одновременно на любом из этажей.
Ответ: а) 1/216; б)1/36.
1.68. В группе 30 человек, из которых 6 отличников. Группа случайным образом разбита на две равные подгруппы. Какова вероятность того, что в каждой подгруппе по три отличника?
Ответ: 0,349.
1.69. При испытании партии приборов относительная частота годных приборов оказалась равной 0.9. Найти число годных приборов, если всего было проверено 200 приборов.
Ответ: 180.
1.70. При стрельбе была получена частота попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов?
Ответ: п = 30.
1.71. Отдел технического контроля обнаружил 6 бракованных деталей в партии из случайно отобранных 60 деталей. Найти относительную частоту появления брака.
Ответ: 0,1.
1.72. Двое студентов договорились встретиться в интервале времени от 9.00 до 10.00. Каждый пришедший ожидает встречи 15 минут, затем уходит. Какова вероятность того, что встреча произойдет?
Ответ: 7/16. Указание: Обозначить время прихода одного студента х, второго у и рассмотреть геометрическую вероятность выполнения неравенства 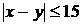 в квадрате со сторонами
в квадрате со сторонами 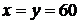 .
.
1.73. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода – один час, а второго – два часа.
Ответ: 0,12.
1.74. Какова вероятность, не целясь, попасть бесконечно малой пулей в прутья квадратной решетки, если толщина прутьев равна 10мм, а расстояние между их осями равно 100мм?
Ответ: ≈ 0,19.
1.75. В шкафу находятся 10 пар ботинок различных сортов. Из них случайно выбирают 4 ботинка. Найти вероятность того, что среди выбранных ботинок отсутствуют парные.
Ответ: 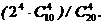
1.76. Среди 25 экзаменационных билетов 5 «легких». Два студента берут по очереди по одному билету. Найти вероятности событий: а) первый студент взял «легкий» билет; б) второй студент взял «легкий» билет; в) оба студента взяли «легкие» билеты.
Ответ: а) 0,2; б) 0,2; в) 0,0333.
1.77. На шахматную доску из 64 клеток наудачу ставятся две ладьи белого и черного цвета. С какой вероятностью они будут бить друг друга?
Ответ: 2/9.
Дата добавления: 2018-05-13; просмотров: 2379; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
