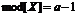Законы распределения дискретных случайных величин.
Биномиальное распределение
Говорят, что дискретная случайная величина X распределена по биномиальному закону, если возможные значения этой случайной величины 0, 1, 2,…, n, а вероятность каждого из значений определяется по формуле Бернулли
 , m = 0, 1, 2,…, n. (23)
, m = 0, 1, 2,…, n. (23)
где 0 £ p £ 1; q = 1 – p.
Постоянные pи n, входящие в формулу (21), называются параметрами биномиального распределения.
На практике биномиальное распределения возникает при следующих условиях: пусть производится серия из n независимых испытаний, в каждом из которых событие A может осуществиться с вероятностью p. Тогда случайная величина X, определяющая число появлений события A в серии из n испытаний, распределена по биномиальному закону.
Биномиальное распределение широко используется при выборочном методе контроля продукции, т.к. определяет вероятность извлечения из партии продукции заданного количества бракованных изделий при известной доле брака.
Закон называется «биномиальным» потому, что правую часть равенства (24) можно рассматривать как общий член разложения бинома Ньютона:
 . (24)
. (24)
Ряд распределения случайной величины X, распределенной по биномиальному закону, имеет вид:
| xi | 0 | 1 | … | k | … | n – 1 | n |
| pi | qn | npqn-1 | … | Cnkpkqn-k | … | npn-1q | pn |
Для случайной величины, распределенной по биномиальному закону,
|
|
|
M[X] = np, D[X] = npq,  . (25)
. (25)
 случайной величины Х, распределенной по биномиальному закону, является целое число k*, удовлетворяющее системе неравенств:
случайной величины Х, распределенной по биномиальному закону, является целое число k*, удовлетворяющее системе неравенств:
np – q £ k* £ np + p.
Пример 14По каналу связи передается 5 сообщений. Каждое сообщение с вероятностью 0,1 независимо от других искажается. Случайная величина X – число искаженных сообщений. Построить ряд распределения этой случайной величины, вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение непосредственно по ряду распределения и сравнить со значениями, которые получаются при использовании формул (25). Найти вероятность того, что будет искажено не более одного сообщения.
Решение. Условие задачи соответствует проведению n = 5 независимых испытаний, в каждом из которых с вероятностью p = 0,1 может осуществиться событие A = {искажение передаваемого сообщения}. Случайная величина X, обозначающая число искаженных сообщений, распределена по биномиальному закону. Возможные значения этой случайной величины: 0, 1, 2, 3, 4, 5. Вероятности возможных значений случайной величины определяются по формуле Бернулли:
|
|
|
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Ряд распределения имеет вид:
| xi | 0 | 1 | 2 | 3 | 4 | 5 | Итого |
| pi | 0,59049 | 0,32805 | 0,0729 | 0,0081 | 0,00045 | 0,00001 | 1 |
Убедимся, что  .
.
Вычислим числовые характеристики данной случайной величины:
| xi | 0 | 1 | 2 | 3 | 4 | 5 | Итого |
| pi | 0,59049 | 0,32805 | 0,0729 | 0,0081 | 0,00045 | 0,00001 | 1 |

| 0 | 0,32805 | 0,1458 | 0,0243 | 0,0018 | 0,00005 | 0,5 |

| 0 | 0,32805 | 0,2916 | 0,0729 | 0,0072 | 0,00025 | 0,7 |

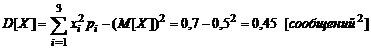 ;
;
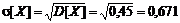 [сообщений];
[сообщений];
xmod = 0 [сообщений].
Вычислим числовые характеристики этой случайной величины по формулам (25):
M[X] = n p = 5 × 0,1 = 0,5;
D[X] = n p q = 5 × 0,1 × 0,9 = 0,45;
 ;
;
Определим моду: 5 × 0,1–0,9 £ k* £ 5 × 0,1+0,1.
–0,4 £ k* £ × 0,6.
xmod = 0.
Как и следовало ожидать, получены точно такие же значения.
Вероятность того, что будет искажено не более одного сообщения,
P(X £ 1) = P(X = 0) + P(X = 1) = 0,59049 + 0,32805 = 0,91854.
Геометрическое распределение
На практике геометрическое распределение возникает при следующих условиях: пусть производится серия независимых опытов, в каждом из которых может произойти событие А с одной и той же вероятностью p. Опыты продолжаются до первого появления события А. Тогда случайная величина X, определяющая число неудач, предшествующих успеху, распределена по геометрическому закону.
|
|
|
Возможные значения этой случайной величины: 0, 1, 2, …, n, …, а вероятность каждого из этих значений определяется по формуле
 , m = 0, 1, 2, …, n, … (26)
, m = 0, 1, 2, …, n, … (26)
где 0 £ p £ 1; q = 1 – p;.
Геометрическое распределение зависит от параметра p.
Замечание– Геометрическая прогрессия – это числовая последовательность a1, a2,…, an,…, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему, умноженному на одно и то же, не равное нулю, число, называемое знаменателем геометрической прогрессии q,
 ,
,  , …,
, …,  .
.
Сумма бесконечно убывающей (q < 1) геометрической прогрессии  .
.
Условие  выполняется, так как принимая во внимание условие сходимости геометрического ряда
выполняется, так как принимая во внимание условие сходимости геометрического ряда  , (
, (  ) и формулу
) и формулу  для его суммы, получаем
для его суммы, получаем 
Ряд распределения случайной величины X, имеющей геометрический закон:
| xi | 0 | 1 | 2 | … | m | … | n | … |
| pi | p | q1 p | q2 p | … | qm p | … | qn p | … |
Для случайной величины, распределенной по геометрическому закону,
 ,
, 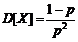 ,
, 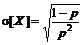 ,
, 
Пример 15Вероятность изготовления нестандартного изделия при некотором технологическом процессе равна 0,06. Контролер берет из партии изделие и сразу проверяет его качество. Если оно оказывается нестандартным, то дальнейшие испытания прекращаются, а партия задерживается. Если же изделие оказывается стандартным, то контролер проверяет следующее изделие и т. д. Записать закон распределения случайной величины X – числа стандартных изделий, проверенных до выявления брака.
|
|
|
Решение. Условие задачи соответствует проведению независимых испытаний, в каждом из которых с вероятностью p = 0,06 может осуществиться событие A = {обнаружено нестандартное изделие}. В этом случае неудача – обнаружение стандартного изделия, успех – обнаружение нестандартного изделия. Случайная величина X – число стандартных изделий, проверенных до выявления брака, распределена по геометрическому закону. Возможные значения этой случайной величины: 0, 1, 2, 3, …, m, …. По условию p = 0,06, q = 1 – 0,06 = 0,94.
Вероятности значений определяются по формуле (26):
 (то есть нестандартное изделие будет обнаружено сразу же при проверке первого изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 0);
(то есть нестандартное изделие будет обнаружено сразу же при проверке первого изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 0);
 (то есть нестандартное изделие будет обнаружено при проверке второго изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 1);
(то есть нестандартное изделие будет обнаружено при проверке второго изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 1);
 (то есть нестандартное изделие будет обнаружено при проверке третьего изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 2) и т. д.
(то есть нестандартное изделие будет обнаружено при проверке третьего изделия, при этом число стандартных изделий, проверенных до появления брака, будет равно 2) и т. д.
Закон распределения можно записать в виде  , или в виде ряда распределения случайной величины X:
, или в виде ряда распределения случайной величины X:
| xi | 0 | 1 | 2 | … | m | … | n | … |
| pi | 0,06 | 0,0564 | 0,053016 | … | 
| … | 
| … |
Распределение Пуассона
Говорят, что дискретная случайная величина X распределена по закону Пуассона, если ее возможные значения: 0, 1, 2, …, m,… (счетное множество значений), а соответствующие им вероятности задаются формулой
 , m = 0, 1, 2, …, (27)
, m = 0, 1, 2, …, (27)
где  .
.
Таблица значений вероятности для различных значений  и
и  приведена в приложении В.
приведена в приложении В.
Таким образом, ряд распределения случайной величины X, распределенной по закону Пуассона, имеет вид:
| xi | 0 | 1 | 2 | … | k | … |
| pi | e– a | ae– a | (a2e– a)/2! | … | (ake– a)/k! | … |
Закон распределения Пуассона зависит от одного параметра: a. Доказано, что для случайной величины, распределенной по закону Пуассона,
M[X] = a, D[X] = a, 
Если a целое число, то случайная величина Х, распределенная по закону Пуассона имеет две моды, a и a-1. Если a дробное число, то мода равна целой части a.
Рассмотрим условия, при которых возникает распределение Пуассона.
1 Распределение Пуассона с параметром a = np можно приближенно применять вместо биномиального распределения, когда число испытаний n достаточно велико, а вероятность появления события в каждом испытании p очень мала (p < 0,1), то есть в каждом отдельном опыте событие A появляется крайне редко. Отсюда происходит использующееся еще иногда для закона Пуассона название «закон редких событий».
2 По закону Пуассона распределена случайная величина, описывающая число событий простейшего потока, произошедших в течение промежутка времени t.
Простейший поток событий.Потоком событий называется последовательность однородных событий, наступающих одно за другим в случайные моменты времени.
Интенсивностью потока l называется среднее число событий, происходящих за единицу времени.
Если l = const, то поток называется стационарным. Это свойство означает, что вероятность наступления того или иного числа событий в течение отрезка времени длиной t не зависит от расположения на оси времени этого отрезка, а зависит только от его длины.
Поток называется ординарным, если вероятность попадания на малый участок Dt двух и более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события. Грубо говоря, это означает, что события возникают поодиночке, а не группами по два, по три и т. д.
Поток событий называется потоком без последействия, если вероятность попадания того или иного числа событий на какой-то отрезок времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним участок, то есть предыстория потока не сказывается на вероятности появления событий в ближайшем будущем. Эта независимость физически сводится к тому, что события появляются на оси времени в силу случайных причин, индивидуальных для каждого из них.
Поток, обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим.
Доказано, что для простейшего потока число событий, попадающих на каждый отрезок времени длиной t, распределено по закону Пуассона с параметром a = lt, где l – интенсивность потока.
Пример 16 По данным длительной проверки качества запчастей определенного вида брак составляет 1%. Найти вероятность того, что в партии из 400 запчастей: а) 5 запчастей окажутся бракованными; б) не более 4 запчастей окажутся бракованными; в) более 4 запчастей окажутся бракованными.
Решение. Случайная величина X, определяющая число бракованных запчастей в партии из 400 запчастей, может принимать значения 0, 1, 2, …, 400. Определим событие В = {в партии из 400 запчастей 5 запчастей окажутся бракованными}.
Так как число испытаний велико, а вероятность наступления события А = {запчасть определенного вида окажется бракованной} очень мала (p = 0,01 < 0,1), то в этом случае можно воспользоваться приближенной формулой Пуассона

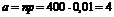 .
.
Определим событие С = {в партии из 400 запчастей не более 4 запчастей окажутся бракованными, то есть или 0, или 1, или 2, или 3, или 4}.
Воспользуемся приближенной формулой Пуассона и теоремой сложения вероятностей несовместных событий:





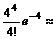 0,0183 + 0,0733 + 0,1465 + 0,1954 +
0,0183 + 0,0733 + 0,1465 + 0,1954 +
+ 0,1954 = 0,6289.
Определим событие D ={ в партии из 400 запчастей более 4 запчастей окажутся бракованными, то есть или 5, или 6, или 7, или 8, …}.
События С и D – противоположные, то есть С È D= 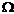 ,Р(С)+Р(D) = 1,
,Р(С)+Р(D) = 1,
Р(D)= 1 – Р(С)= 1 – 0,6289 = 0,3711.
Пример 17 К абоненту АТС в среднем поступает 1,5 вызова в час. Поток вызовов можно считать простейшим. Для этого промежутка времени найти вероятность того, что: а) в течение часа поступит хотя бы один вызов; б) в течение трех часов произойдет не менее четырех вызовов.
Решение. а) Случайная величина X1, определяющая число вызовов, поступивших в течение часа, может принимать значения 0, 1, 2, 3,… и, согласно условию, распределена по закону Пуассона с параметром a = l t = 1,5 (так как интенсивность потока l = 1,5; t = 1[час]). Обозначим событие: A= {в течение часа поступит хотя бы один вызов}.
Тогда
P(A) = P(X1 ³ 1) = 1 – P(X1 = 0) = 1 – (a0e–a)/0! = 1 – е–1,5 = 1 – 0,22313 =0,77687.
б) Для определения вероятности события B = {в течение трех часов поступит не менее четырех вызовов} введем в рассмотрение случайную величину X2, определяющую число вызовов, поступивших в течение трех часов. Эта случайная величина распределена по закону Пуассона с параметром a = l t = 1,5 × 3 = 4,5:

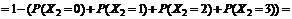

В таблице 2 представим некоторые виды дискретных законов распределения.
Таблица 2 – Некоторые виды дискретных законов распределения
| Вид закона распределения | |||
| Биномиальный закон | Геометрический закон | Закон Пуассона | |
| Возможные значения | |||
| Х: 0, 1, 2, …, n | Х: 0, 1, 2, …, m, …, | Х: 0, 1, 2, …, m,… | |
| Формула для вычисления вероятности | |||

| 
|
| |
| Столбцовая диаграмма | |||

|
| 
| |
| Основные числовые характеристики дискретных случайных величин | |||
| Математическое ожидание дискретной случайной величины
Дисперсия дискретной случайной величины
Среднее квадратическое отклонение
| |||
| Биномиальный закон | Геометрический закон | Закон Пуассона | |
M[X] = np, D[X] = npq,
 .
Мода – целое число, удовлетворяющее неравенству
np – q £ m0 £ np + p, .
Мода – целое число, удовлетворяющее неравенству
np – q £ m0 £ np + p,
|  , ,   , , 
|
M[X] = a, D[X] = a, если a целое число, то мода | |
| Примеры случайных величин, распределенных по закону | |||
| 1 Число появлений герба при четырех подбрасываниях монеты (Х: 0, 1, 2, 3, 4); 2 Число бракованных деталей из наудачу выбранных 3 (при условии, что вероятность брака для каждой детали одинаковая) (Х: 0, 1, 2, 3) | 1 Игральная кость подбрасывается до первого появления цифры 6. Х – число «неудачных» подбрасываний. Х: 0,1,2…; 2 Охотник стреляет в цель до первого попадания. Х – число «неудачных» выстрелов. Х: 0,1,2…n…. | 1 Число вызовов, поступающих на станцию скорой помощи в течение часа. Х: 0, 1, 2, …, m,… 2 Поток железнодорожных составов, прибывающих на станцию в течение часа. Х: 0, 1, 2, …, m,… | |
Дата добавления: 2018-05-12; просмотров: 1001; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!



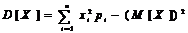


 и
и