Числовые характеристики случайных величин

⇐ ПредыдущаяСтр 5 из 10Следующая ⇒

Закон распределения полностью характеризует случайную величину. Кроме того, в теории вероятностей широко используются некоторые «типичные значения», которые характеризуют случайную величину суммарно. Эти числа, описывающие некоторые характерные черты распределения, называются числовыми характеристиками.

Важнейшей числовой характеристикой положения случайной величины является математическое ожидание.

1 Математическое ожидание характеризует среднее значение случайной величины. Термин «математическое ожидание» связан с начальным периодом развития теории вероятностей, когда она развивалась на примерах и задачах азартных игр и игрока интересовал средний выигрыш, то есть среднее значение ожидаемого выигрыша. Для дискретных и непрерывных случайных величин математическое ожидание вычисляется, соответственно, по формулам (17) и (18) (при условии, что ряд в формуле (17) и интеграл в формуле (18) сходятся абсолютно):

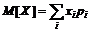; (17)

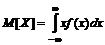. (18)

В механической интерпретации математическое ожидание характеризует центр тяжести системы.

Свойства математического ожидания:

а)математическое ожидание постоянной величины равно этой постоянной:

M[C] = C;

б)постоянный множитель можно выносить за знак математического ожидания:

M[CX] = C M[X];

в)математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий.

Например, для трех случайных величин X₁, X₂, X₃

M[X₁± X₂± X₃] = M[X₁] ± M[X₂] ± M[X₃];

г) если 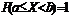, то M[X] 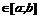, то есть математическое ожидание произвольной случайной величины X принадлежит интервалу между минимальным и максимальным возможными значениями случайной величины X;

д)математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий. Например, для трех независимых случайных величин X₁, X₂, X₃

M[X₁X₂X₃] = M[X₁] M[X₂] M[X₃].

2 Модой дискретной случайной величины X (обозначается x_mod) называется ее наиболее вероятное значение, то есть то значение, для которого вероятность p_i достигает максимума. Моду дискретной случайной величины можно определить графически по столбцовой диаграмме, как абсциссу столбца, имеющего наибольшую высоту.

Модой непрерывной случайной величины X (обозначается x_mod) называется то ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два максимума, то распределение называется двумодальным.

Замечание – Рассмотрим функцию 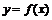, областью определения которой является промежуток 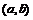. Если можно указать такую 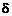– окрестность точки 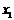, принадлежащую промежутку 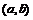, что для всех 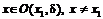, выполняется неравенств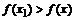о , то 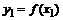называют локальным максимумом функции 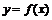. Максимум функции имеет локальный характер (это наибольшее значение функции в достаточно малой окрестности соответствующей точки).

3 Медианой случайной величины X называется такое ее значение x_med, для которого P(X < x_med) = P(X ³ x_med) = 0,5, то есть одинаково вероятно, примет ли случайная величина значение, большее или меньшее медианы.

Для непрерывной случайной величины геометрически: медиана – это координата той точки на оси абсцисс, для которой площади фигур, ограниченных кривой f(x) и осью абсцисс, находящихся слева и справа от неё, одинаковы и равны 0,5. Учитывая определение функции распределения, .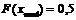

Эта характеристика применяется, как правило, только для непрерывных случайных величин. Для дискретных случайных величин множество значений х, удовлетворяющих свойству медианы 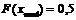, может быть либо бесконечно, либо является пустым.

Очевидно, что характеристики положения (математическое ожидание, мода и медиана) имеют такую же размерность, как и сама случайная величина.

4 Дисперсия является мерой рассеивания значений случайной величины относительно ее математического ожидания. Для дискретных и непрерывных случайных величин дисперсию можно вычислить соответственно по формулам

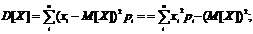(19)

(20)

В механической интерпретации дисперсия представляет собой момент инерции распределения масс относительно центра масс (математического ожидания). Если говорить о форме кривой плотности распределения, то дисперсия характеризует степень ее «размазанности» по оси Ox. Чем больше величина D[X], тем более «размазанным» выглядит соответствующее распределение.

Свойства дисперсии:

а)дисперсия постоянной величины равна нулю:

D[C] = 0;

б)постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D[CX] = C²D[X];

в)дисперсия алгебраической суммы нескольких независимых случайных величин равна сумме их дисперсий. Например, для трех случайных величин X₁, X₂и X₃

D[X₁± Х₂± Х₃] = D[X₁] + D[Х₂] + D[Х₃];

г) дисперсия алгебраической суммы случайной величины Х и постоянной величины С равна дисперсии случайной величины Х

D[С ± Х] = D[X].

5 Для того чтобы получить характеристику разброса значений случайной величины относительно математического ожидания, имеющую такую же размерность, как и сама случайная величина, используют корень квадратный из дисперсии, взятый с положительным знаком. Полученная величина называется средним квадратическим отклонением (или стандартным отклонением) и обозначается 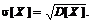Чем больше разброс значений случайной величины Х вокруг М[Х], тем больше 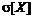и .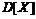

Как следует из определения, размерность дисперсии равна квадрату размерности случайной величины. Так, если случайная величина имеет размерность «вагон», то математическое ожидание, мода и медиана имеют размерность «вагон», дисперсия имеет размерность «вагон²», а среднее квадратическое отклонение имеет размерность «вагон».

Часто используются две безразмерные числовые характеристики, описывающие скошенность и островершинность графика функции плотности распределения вероятностей.

6 Коэффициент асимметрии (обозначается A[X]) характеризует скошенность распределения случайной величины относительно математического ожидания. Для симметричных относительно математического ожидания распределений A[X] = 0. Если в распределении случайной величины преобладают положительные отклонения, то A[X] > 0, если отрицательные, то A[X] < 0.

На рисунке 3 изображены графики функций плотности распределения вероятностей с положительным и отрицательным значениями A[X], а также график симметричного распределения. Значение коэффициента асимметрии для дискретных и непрерывных случайных величин вычисляется, соответственно по формулам

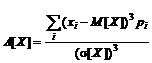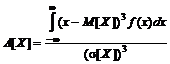; . (21)

7 Коэффициент эксцесса (обозначается Ex[X]) характеризует островершинность графика функции плотности распределения вероятностей f(x). Своеобразным началом отсчета при измерении степени островершинности служит нормальное распределение, для которого Ex[X] = 0.

Как правило, распределения с более высокой и более острой вершиной кривой плотности распределения (или многоугольника распределения) имеют положительное значение коэффициента эксцесса, а с более низкой и пологой – отрицательное значение.

На рисунке 4 приведены графики функции плотности нормального распределения, а также распределений, имеющих положительное и отрицательное значения коэффициента эксцесса.


Рисунок 3 – Графики функции плотности нормального распределения при различных A[X]	Рисунок 4 – Графики функции плотности нормального распределения при различных Ex[X]

Для вычисления значений коэффициента эксцесса дискретных и непрерывных случайных величин используются следующие формулы:

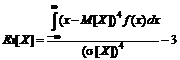; (22).

Пример 12 Для определённой в условии задачи дискретной случайной величины:

а) построить ряд распределения и столбцовую диаграмму;

б) вычислить числовые характеристики: математическое ожидание, моду, дисперсию и среднее квадратичное отклонение.

В цехе работают три автоматических станка, изготавливающиходнотипные детали. Вероятности изготовления детали высшего сорта для каждого из трех станков, соответственно равны: 0,7; 0,6; 0,8. С каждого станка наудачу выбраны по одной детали. Случайная величина X – число деталей высшего сорта из трех наудачу выбранных.

Решение.а) Возможные значения данной случайной величины X: 0, 1, 2, 3. Условие задачи можно рассматривать как серию из n = 3 независимых испытаний. В данном случае для вычисления вероятностей возможных значений случайной величины X можно воспользоваться теоремами сложения вероятностей несовместных событий и умножения вероятностей независимых событий:

Обозначим события:

A_i = {с i-го станка выбрана деталь высшего сорта}, i = 1, 2, 3.

Согласно условию вероятность события A₁ P(A₁) = 0,7, вероятность события A₂ P(A₂) = 0,6, вероятность события A₃ P(A₃) = 0,8. Тогда вероятности противоположных событий:

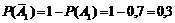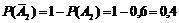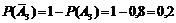Определим все возможные события данного случайного эксперимента и соответствующие вероятности:

События	Вероятности








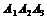
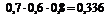
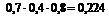
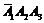
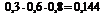
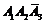
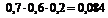
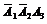
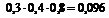
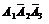
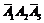
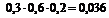
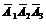
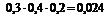
Итого	1

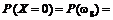
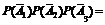
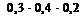= 0,024;

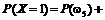
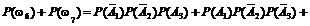
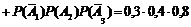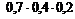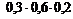+ + = 0,096 + + 0,056 + 0,036 = 0,188;

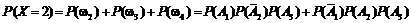
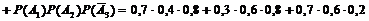= 0,224 + + 0,144 +0,084 = 0,452;

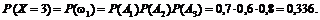
(Проверим, что ).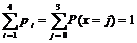

Ряд распределения данной случайной величины X:

x_i	0	1	2	3	Итого
p_i	0,024	0,188	0,452	0,336	1

Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 5.

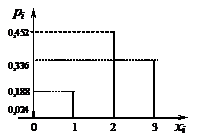
Рисунок 5 – Столбцовая диаграмма

б) Вычислим функцию распределения данной случайной величины:

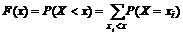при x Î (- ¥, 0] ;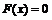

при x Î (0, 1] ;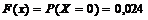

при x Î (1, 2] ;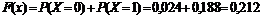

при x Î (2, 3]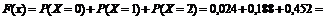

;

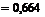при x Î (3, +¥)

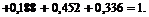
Итак, функция распределения рассматриваемой случайной величины

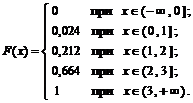
График функции F(x) приведён на рисунке 6.

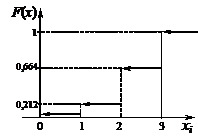
Рисунок 6 – Функция распределения

б) Вычислим числовые характеристики данной случайной величины.

Составим таблицу:

x_i	0	1	2	3	Итого
p_i	0,024	0,188	0,452	0,336	1
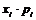
	0	0,188	0,904	1,008	2,1
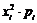
	0	0,188	1,808	3,024	5,02

Математическое ожидание

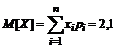[деталей], то есть среднее число деталей высшего сорта из наудачу выбранных трех, равно 2,1.

Как следует из ряда распределения, данная случайная величина имеет моду 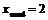[деталей], (для x_i = 2 вероятность принимает максимальное значение p_i= 0,452), то есть наиболее вероятное число деталей высшего сорта из наудачу выбранных трех, равно 2.

Дисперсия 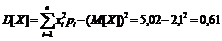[деталей²].

Среднее квадратическое отклонение 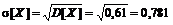[деталей], то есть среднее квадратическое отклонение числа деталей высшего сорта из наудачу выбранных трех, равно 0,671.

Пример 13Закон распределения непрерывной случайной величины задан функцией плотности распределения вероятностей f(x). Требуется:

а) построить график функции плотности распределения вероятностей;

б) вычислить числовые характеристики данной случайной величины: математическое ожидание, моду, медиану, дисперсию, среднее квадратичное отклонение;

в) найти вероятность того, что данная случайная величина примет значение, принадлежащее отрезку [a; b]:

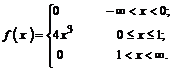а = 0, b = 0,5.

Решение. а) График функции f(x) изображён на рисунке 7.

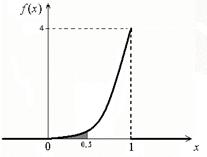
Рисунок 7 – График плотности распределения f(x)

б) Вычислим функцию распределения данной случайной величины:

при x Î (- ¥, 0] ;

при x Î (0, 1] ;

при x Î (1, + ¥) .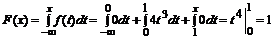

Итак,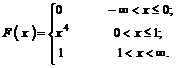

График функции F(x) приведён на рисунке 8.

Рисунок 8 – График функции распределения F(x)

в) Вычислим числовые характеристики данной случайной величины.

Математическое ожидание

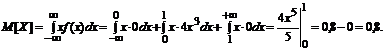
Для вычисления дисперсии воспользуемся формулой

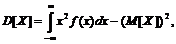
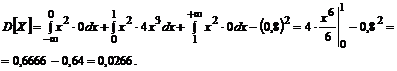
Среднее квадратическое отклонение .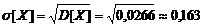

Мода данной случайной величины, как следует из графика функции f(x), равна 1.

Для определения медианы воспользуемся соотношением

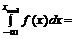
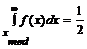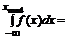
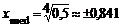По условию плотность распределения случайной величины не равна 0 в интервале 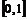, поэтому .

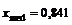Медиану также можно определить из соотношения F(x_med) = 0,5.

Решая уравнение 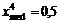, получим .

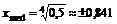По условию плотность распределения случайной величины равна 0 на отрезке 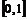, поэтому .

г) Для вычисления вероятности того, что случайная величина Х примет значение, принадлежащее отрезку [0; 0,5], можно воспользоваться, например, соотношением ,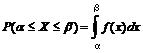

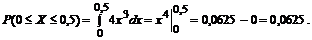
На рисунке 7 штриховкой выделена фигура, площадь которой равна вероятности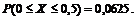

Вопросы для самоконтроля

1 Что называется случайной величиной?

2 Какие величины называются дискретными? непрерывными?

3 Что называется законом распределения случайной величины?

4 Какими способами может быть задан закон распределения дискретной случайной величины? непрерывной?

5 Что характеризует функция распределения F(x) случайной величины?

6 Что характеризует функция плотности распределения случайной величины? Укажите ее вероятностный смысл.

7 Для каких величин определена функция плотности распределения?

8 Как связаны между собой функции F(x) и f(x)?

9 Как определить вероятность попадания значения непрерывной случайной величины в некоторый интервал с помощью функции плотности распределения?

10 Как определяется математическое ожидание дискретной случайной величины?

11 Как определяется математическое ожидание непрерывной случайной величины?

12 Что такое среднее квадратическое отклонение?

2.4 Некоторые наиболее важные для практики распределения
случайных величин

Наиболее часто используемые законы распределения случайных величин:

для дискретных случайных величин – это:

– биномиальное распределение;

– распределение Пуассона;

–геометрическое распределение;

для непрерывных случайных величин – это:

– равномерное (прямоугольное) распределение;

– показательное (экспоненциальное) распределение;

– нормальное распределение (распределение Гаусса).

Дата добавления: 2018-05-12; просмотров: 1123; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!