Дискретные и непрерывные случайные величины

Одним из понятий случайной величины является понятие случайной величины.

Случайной величиной называется величина, которая при повторении некоторого эксперимента в одинаковых условиях может принимать различные значения, причем заранее неизвестно, какое из них.

Случайные величины принято обозначать прописными буквами латинского алфавита: X, Y, Z, …, либо буквами греческого алфавита: x, h, q, …, а их значения – строчными буквами латинского алфавита: x, y, z.

Дискретной называется случайная величина Х, которая в результате эксперимента Е может принимать конечное или счетное число значений. Примеры дискретных случайных величин: число студентов в группе, успешно сдавших экзамен по математике; число клиентов банка, своевременно возвративших кредит; число звонков, поступивших в справочную службу вокзала в течение часа, число и т. д.

Случайные величины, возможные значения которых непрерывно заполняют некоторый (конечный или бесконечный) промежуток числовой оси, называются непрерывными. Множество возможных значений непрерывных случайных величин является несчетным множеством.

Примеры непрерывных случайных величин: время безотказной работы оборудования после очередного ремонта; время простоя клиента магазина в очереди; масса израсходованного автомобилем бензина на одном и том же расстоянии; отклонение размера изделия от номинала.

Закон распределения случайной величины

Законом распределения дискретной случайной величины называется соответствие между значениями этой величины и их вероятностями

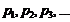
Закон распределения дискретной случайной величины может быть задан таблично или аналитически (то есть с помощью формул).

Очевидно, что для полного описания исследуемого вероятностного эксперимента (то есть для исчерпывающего задания характеризующей его случайной величины) недостаточно задать только пространство элементарных событий W. К этому необходимо добавить также:

а) для дискретной случайной величины (ДСВ) – правило, сопоставляющее каждому возможному значению случайной величины х_i вероятность того, что случайная величина X примет в результате эксперимента это значение:

;

б) для непрерывной случайной величины (НСВ) – правило, позволяющее поставить в соответствие любой измеримой области DX возможных значений случайной величины X вероятность попадания значения случайной величины в эту область:

Дадим общее определение: законом распределения случайной величины X называется любое соотношение, устанавливающее связь между возможными значениями этой случайной величины и соответствующими им вероятностями.

Закон распределения случайной величины Х может быть задан таблично, графически и аналитически (таблица 3).

Таблица 2 –Способы задания законов распределения случайных величин

Табличный	Графический		Аналитический
Ряд распределения	Столбцовая диаграмма	Многоугольник распределения	Непосредственная формула	Функция распределения	Функция плотности распределения
ДСВ	ДСВ	ДСВ	ДСВ, НСВ	ДСВ, НСВ	НСВ

Ряд распределения

Пусть X – дискретная случайная величина, а x₁, x₂, x₃,… – ее значения. Совокупность всех элементарных событий, на которых X принимает фиксированное значение x_i, образует событие X = x_i.

Простейшим способом задания закона распределения дискретной случайной величины является ряд распределения. Это таблица, в первой строке которой указаны возможные значения случайной величины x₁, x₂, x₃, …, а во второй – соответствующие им вероятности p₁, p₂, p₃,…, где p_i = P(X = x_i) – вероятность того, что в результате эксперимента случайная величина X примет значение x_i:

x_i	x₁	x₂	x₃	…
p_i	p₁	p₂	p₃	…

Так как события (X = x₁), (X = x₂), … – несовместны, и их объединение представляет собой все пространство элементарных событий, то сумма вероятностей р_i равна 1:

. (14)

Графическое изображение ряда распределения может быть представлено одним из двух способов: в виде столбцовой диаграммы и в виде многоугольника распределения.

Рисунок 1 – Графические способы задания законов распределения

дискретной случайной величины

Столбцовая диаграмма строится следующим образом: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения.

При построении многоугольника распределения по оси абсцисс откладываются возможные значения случайной величины, по оси ординат – соответствующие им вероятности, и полученные соседние точки соединяются отрезками.

Функция распределения

Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.

Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть

F(x) = P(X < x).

Основные свойства функции распределения F(x):

1Так как по определению F(x) равна вероятности события, все возможные значения функции распределения принадлежат отрезку [0; 1]:

0 £ F(x) £ 1.

2Если , то , то есть F(x) – неубывающая функция своего аргумента.

3Вероятность того, что случайная величина примет значение, принадлежащее полуинтервалу [ 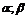), равна приращению функции распределения на этом интервале:

P( £ X < ) = F( ) – F( ).

4Если все возможные значения случайной величины принадлежат отрезку [a, b], то

F(x) = 0, при x £ a; F(x) = 1, при x > b.

Функция распределения дискретных случайных величинможет быть определена по формуле

. (15)

Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения.

В общем случае, функция распределения F(x) дискретной случайной величины X есть разрывная ступенчатая функция, непрерывная слева, скачки которой происходят в точках, соответствующих возможным значениям х₁, х₂, … случайной величины X и равны вероятностям p₁, p₂, … этих значений.

Пример 11 Вычислить и построить функцию распределения для дискретной случайной величины, закон распределения которой, имеет вид:

x_i	0,1	1,2	2,3	4,5
p_i	0,1	0,2	0,6	0,1

Решение. Определим значения функции F(x) = P(X < x) для всех возможных значений x:

при x Î (– ¥; 0,1] нет ни одного значения случайной величины X, меньшего данных значений x:

F(x) = 0;

при x Î (0,1; 1,2] только одно возможное значение (X = 0,1) меньше рассматриваемых значений x. То есть при x Î (0,1; 1,2] F(x) = P(X = 0,1) = 0,1;

при x Î (1,2; 2,3] два значения (X = 0,1 и X = 1,2) меньше данных значений x, следовательно, F(x) = P(X = 0,1) + P(X = 1,2) = 0,1 + 0,2 = 0,3;

при x Î (2,3; 4,5] три значения (X = 0,1, X = 1,2 и X = 2,3) меньше данных значений x, следовательно, F(x) = P(X = 0,1) + P(X = 1,2) + P(X = 2,3) = 0,1 + 0,2 + 0,6 = 0,9 ;

при x Î (4,5, ¥) все возможные значения случайной величины X будут меньше данных значений x, и F(x) = P(X = 0,1) + P(X = 1,2) + P(X = 2,3) +

+ P(X = 4,5) = 0,1 + 0,2 + 0,6 + 0,1 = 1.

Таким образом,

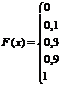
График функции F(x) изображен на рисунке 2.

Рисунок 2 – Функция распределения

Функция распределения непрерывных случайных величин.Теперь можно дать более точное определение непрерывных случайных величин: случайная величина X называется непрерывной, если ее функция распределения F(x) при всех значениях x непрерывна и, кроме того, имеет производную 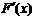всюду, за исключением, может быть, отдельных точек.

Из непрерывности функции F(x) следует, что вероятность каждого отдельного значения непрерывной случайной величины равна нулю.

Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид

P(a £ X < b) = P(a £ X £ b) = P(a < X £ b) = P(a < X < b) = F(b) – F(a). (16)

2.2.3 Функция плотности распределения вероятностей
непрерывной случайной величины

Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке:

f(x) = F ¢(x).

По своему смыслу значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x.

Функция плотности распределения f(x), как и функция распределения F(x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f(x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F(x) называют, соответственно, интегральной функцией распределения.

График функции плотности распределения f(x) называется кривой распределения.

Рассмотрим свойства, которыми обладает функция плотности распределения непрерывной случайной величины.

Свойство 1.Плотность распределения вероятностей – неотрицательная функция:

f(x) ³ 0

(геометрически: кривая распределения лежит не ниже оси абсцисс).

Свойство 2.Вероятность попадания значения случайной величины на участок от до определяется по формуле

;

(геометрически: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f(x), осью Ох и прямыми x = и x = ).

Свойство 3.

(геометрически: площадь фигуры, ограниченной графиком функции плотности распределения и осью абсцисс, равна единице).

В частности, если все возможные значения случайной величины принадлежат отрезку [ ; ], то

Свойство 4.Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом:

Дата добавления: 2018-05-12; просмотров: 555; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!