Вычисление вероятностей событий по классической формуле определения вероятности»
Учебная цель: научиться вычислять вероятности случайных событий с использованием классической формулы вероятности события.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- вычислять вероятности событий с использованием элементов комбинаторики;
знать:
- основы теории вероятностей и математической статистики;
Краткие теоретические и учебно-методические материалы по теме практической работы
События, явления могут быть достоверными, невозможными и случайными. Те события, которые обязательно произойдут при осуществлении определённой совокупности условий (которую будем называть опытом или испытанием), называют достоверными и обозначают U. Событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий, называют невозможным и обозначают V . События, которые при испытании могут произойти, а могут и не произойти, называют случайными и обозначают - А, В, С.
Случайные события называются несовместными, если каждый раз возможно появление только одного из них. События называются совместными, если в данных условиях появление одного из них не исключает появление другого при том же испытании. События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны. Случайные события бывают элементарные и составные. Множество всех элементарных событий, связанных с некоторым опытом, называется пространством элементарных событий (U). Каждое событие определяется как подмножество во множестве элементарных событий A. При этом те элементарные события из U, при которых событие А наступает (т.е. принадлежит подмножеству А), называются благоприятствующими событию А.
|
|
|
Пусть 
- случайное событие, связанное с некоторым опытом. Повторим опыт 
раз в одних и тех же условиях и пусть при этом событие 
появилось 
раз.Отношение 
числа опытов, в которых событие 
появилось, к общему числу проведённых опытов называется частотой события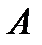 
.
Постоянная величина р, к которой все более приближается частота событий А при достаточно большом повторении опыта, называется вероятностью события А и обозначается 
.
Рассмотрим конечное пространство элементарных событий 
, где 
- попарно несовместные и равновозможные элементарные события. Пусть некоторому событию А благоприятствуют т из п элементарных событий пространства U.
Вероятностью события р(А) называется отношение числа т элементарных событий, благоприятствующих событию А, к общему числу п равновозможных элементарных событий:
|
|
|
(1)
Из определения вероятности вытекают следующие её свойства:
1. Вероятность любого события 
;
2. Вероятность достоверного события 
, так как 
;
3. Вероятность невозможного события 
так как 
Дата добавления: 2018-05-12; просмотров: 763; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!