Основные свойства линейных цепей

⇐ ПредыдущаяСтр 4 из 19Следующая ⇒

Свойство №1.Процессы в простых линейных цепях описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Приведем пример такой цепи. Если имеется простая последовательная цепь, состоящая из сосредоточенных пассивных элементов R, L, и C и источника эдс (рис. 2.1), то процессы в ней описываются уравнением , т. к. , и или после дифференцирования имеем (2.1)

что соответствует указанному выше свойству.

Известно, что систему n уравнений первого порядка можно заменить одним уравнением n-го порядка. В силу этого, для более сложной цепи, состоящей из n простых цепей, справедливо уравнение:

(2.2)

где f(t) – некоторое внешнее воздействие.

Если все параметры a_n являются постоянными, то уравнение (2.2) описывает систему с постоянными параметрами.

Если хотя бы один из параметров a_n является функцией времени, то уравнение (2.2) будет характеризовать систему с переменными параметрами или параметрическую цепь.

Если параметры a_n являются функцией тока или напряжения, то мы будем иметь нелинейную систему.

Свойство линейности элементов можно истолковать как результат линейности их вольтамперных характеристик (w=const).

Свойство №2.Для линейных цепей справедлив принцип независимости при наложении внешних воздействий (принцип суперпозиции). Этот принцип можно проиллюстрировать следующим образом. При действии на линейную систему нескольких внешних сил, поведение системы можно представить путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности. Для простоты рассмотрим цепь, которая при действии на нее силы f₁(t) описывается уравнением (2.3)

Решением этого уравнения будет y₁(t), где y(t) может иметь значение тока, напряжения, заряда и.т. п.

При действии на эту же систему силой f₂(t), процессы будут описываться уравнением

(2.4)

Пусть его решением будет y₂(t)

При одновременном действии на систему сил f₁(t) и f₂(t) уравнение будет иметь вид

(2.5)

Решением его будет y₃(t). Если система линейна, то

y₃(t)=y₁(t)+y₂(t)

(2.6)

Если же система нелинейна, то

y₃(t)¹y₁(t)+y₂(t).

(2.7)

Свойство №3. В линейных системах не происходит преобразования спектра частот. Это свойство является следствием того, что операции интегрирования и дифференцирования являются линейными.

Так, для цепи на рис 2.1, воздействие f(t)=e(t) будет описываться тремя слагаемыми, линейно связанными протекающими по цепи токами с падениями напряжений на резисторе, индуктивности и ёмкости. Тогда , если, например, 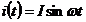, то , ,

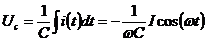
В случае сложного характера f(t), последняя разлагается на элементарные составляющие (в ряд Фурье) и на основании предыдущего принципа суперпозиции, каждая из составляющих даст решение с той же частотой.

В нелинейных цепях всегда происходит процесс преобразования спектра частот сигнала. Это же утверждение справедливо и для параметрических цепей, т. е. цепей с переменными параметрами a=a(t).

В нелинейной системе структура преобразованного сигнала зависит не только от времени но и от амплитуды. Если u₃=u₁+u₂, то i₃¹i₁+i₂.

Дифференцирующие цепи.

С помощью простейших RC- и RL-цепей (рис. 2.3) можно проводить дифференцирование сигналов.

Пусть на вход RC-цепи (рис. 2.3 а) подан сигнал U_вх. Тогда 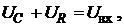но , а U_R=Ri и, следовательно, 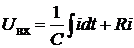(2.11)

Умножая числитель и знаменатель первого слагаемого в правой части уравнения (2.11) на R и учитывая, что напряжение на выходе U_вых=U_R, получим (2.12)

Обозначая далее постоянную времени данной цепи RC=t, а затем дифференцируя обе части уравнения (2.12) по времени t, получим

(2.13)

При условии того, что 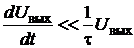, что справедливо, когда tдостаточно мала и что t<<t_и, на основании равенства (2.13) будем иметь 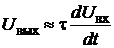(2.14)

из которого следует, что выходное напряжение пропорционально производной от входного, т. е. имеет место процесс дифференцирования сигнала.

Если положить, что tочень велика (t>>t_и), и значением 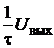по сравнению с можно пренебречь, то на основании соотношения (2.13) получим , откуда U_вых=U_вх и RC-цепь в этих условиях становится переходной, т. е. такой цепью, проходя через которую выходной сигнал повторяет входной. Эта цепь может использоваться, например, для связи между отдельными каскадами многокаскадного усилителя.

Из сказанного выше видно, что дифференцирование будет тем точнее, чем меньше постоянная времени цепи t=RC. Дифференцирующую цепь называют также обостряющей или укорачивающей, так как длительность выходных импульсов меньше длительности входных, а их вершина является острой.

При определении длительности продифференцированных импульсов появляется некоторая неопределенность. Если же величину длительности импульса определять на уровне 0,5U_m, где U_m – его амплитуда, то тогда , откуда , и тогда длительность импульса по уровню 0,5 будет равна (2.15)

Формула (2.15) может быть использована при экспериментальном определении постоянной времени t цепи.

Выражения для комплексного коэффициента передачи дифференцирующей цепи рис.2.3 а имеет вид 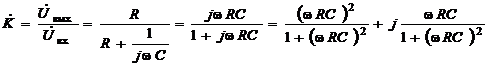(2.16)

АЧХ и ФЧХ такой цепи, как следует из соотношений (2.16), выражаются формулами

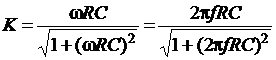	,	(2.17)
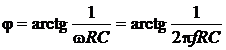	.	(2.18)

Графики выражений (2.17) и (2.18) представлены на рис. 2.4.

Такими же характеристиками обладает RL-цепь, изображенная на рис. 2.3 б спостоянной времени цепи t=L/R.

Если в качестве входного сигнала взять единичный скачок напряжения U_вх(t)=s(t) (рис.2.5 а), то интегрированием уравнения (2.13) можно получить переходную характеристику дифференцирующей цепи или временную зависимость выходного сигнала при единичном скачке напряжения на входе (2.19)

При воздействии на дифференцирующую цепь сигнала прямоугольной формы на выходе получается

напряжение, частный случай

которого представлен на

рис. 2.6. Вид напряжения на

выходе определяется

постоянной времени t=RC.

Интегрирующие цепи.

На рис.2.7. изображены простейшие RC- и RL- интегрирующие цепи.

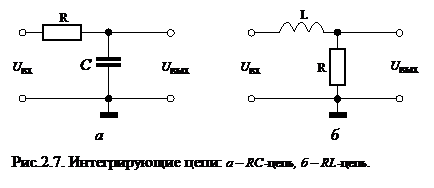Рассмотрим схему, изображенную на рис. 2.7 а. В данном случае выходной сигнал снимается с емкости и уравнение, описывающее рассматриваемую цепь U_вх=Ri+U_вых можно представить в виде

(2.20)

Пусть в равенстве (2.20) tвелика так, что

, тогда получаем , откуда (2.21)

т. е. выходное напряжение пропорционально интегралу от входного, и поэтому с помощью данной цепи выполняется операция интегрирования.

Если же в равенстве (2.20) положить, что tмала и выполняется соотношение ,то можем записать, что (2.22)

В этих условиях цепь называется переходной, т. к. выходной сигнал повторяет входной.

Как следует из (2.21) интегрирование происходит тем точнее, чем больше постоянная времени t. Но увеличение постоянной времени t=RC, как следует из выражения (2.20), ведет к уменьшению величины выходного напряжения, поэтому идеально точное интегрирование с помощью рассмотренной выше цепи невозможно. Условием приближенного интегрирования импульса является неравенство t_и<<t.

Комплексный коэффициент передачи напряжения интегрирующей RC-цепи (рис. 2.7) можно представить в виде

(2.23)

При этом модуль коэффициента передачи выражения (2.23) или другими словами амплитудно-частотная характеристика (АЧХ) цепи будет иметь вид

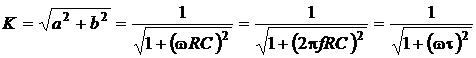(2.24)

где t=RC – постоянная времени цепи.

Фазовый сдвиг между напряжением на выходе и входным напряжением или фазо-частотная характеристика (ФЧХ) цепи определяется выражением

(2.25)

Графики выражений (2.24) и (2.25) представлены на рис.2.8.

Переходная характеристика такой цепи получается интегрированием (2.13) при U_вх=s(t): (2.26)

При равных постоянных времени такими же свойствами обладает RL-цепь с сопротивлением на выходе (рис. 2.7 б).

Частный пример интегрирования прямоугольного импульса представлен на рис. 2.9. Вид напряжения на выходе определяется как и в случае дифференцирующей цепи постоянной времени t.

Дата добавления: 2018-05-12; просмотров: 997; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!