Необходимое условие монотонности
F(x)-дифференцируемая функция; если f(x) – возрастает(убывает), то 

Достаточное условие монотонности
если f(x) – возрастает(убывает), то 
доказательство – формула Лангранжа

Необходимое и достаточное условия существования экстремума функции в точке. Нахождение наибольшего и наименьшего значений функции на отрезке.
Точка Х0 называется точкой локального минимума (максимума) функции f(x), если f(x0)< f(x)(f(x0)>f(x)) для всех точек Х из данной окрестности в точке Х0.
Общее название – локальный экстремум.
Теорема 3. (необходимое условие существования экстремума)
Если дифферинцируемая функция имеет экстремум в точке Х0, то f ‘(x)=0 (следствие теоремы ферма)
Следует: функция может иметь экстремум в точке, в которой производная равна 0 или не существует, такие точки называются критическими.
Теорема 4. (первое достаточное условие существования экстремума).
f(x) дифферинцируема в точке x0 f ‘(x)=0.
Если при переходе через точку x0 производная изменяет знак, то в точке x0 существует экстремум, а именно max, если с + на – и min, если с – на + .
Теорема 5. (второе достаточное условие существования экстремума).
f(x)-дважды дифферинцируема и f ‘(x)=0.
Если f ‘’(x0)<>0, то в точке x0 существует экстремум, причем min, если f ‘’(x0)>0 и max, если f ‘’(x0)<0.
f ‘’(x0)=lim(f’(x0+∆x)- f ‘(x0))/∆x=lim(f ‘(x)/(x-x0)>0 =>
f ‘(x) >0, если x>x0 и
f ‘(x)<0, если x< x0
|
|
|
Асимптоты графика функции и их нахождение
Прямая x=a является вертикальной асимптотой для графика функции f(x), если хотя бы один из пределов:  бесконечен.(x=a – точки разрыва 2-го рода).
бесконечен.(x=a – точки разрыва 2-го рода).
Прямая у=kx+b является асимптотой функции f(x), если функцию можно представить в виде:
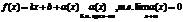
Ищем k и b




Исследование функции на выпуклость. Точки перегиба. Общая схема исследования функции.
Общая схема исследования функции:
1. D (f)-область определения функции. Четность и нечетность.
2. Асимптоты.
3. Исследование функции на монотонность и экстремумы.
4. Исследование функции на выпуклость и точки перегиба.
5. Вычисление значений функции в точках экстремумы, перегиба, некоторых других точках. Точки пересечения с осями координат.
6. Таблица и график.
Исследование функции на выпуклость.
Функция называется выпуклой (вогнутой) на промежутке (А, В), если для любой точки с координатами x и f(x), x€(a,b) график лежит под (над) касательной.
Если f’’(x)<0, f’’(x)>0
Функции нескольких переменных. Частные производные.
Z=x2+y2 - элептический пораболоид
Z=x2-y2 - гиперболический пораболоид
Z=f(x,y) предел: 
Непрерывность 
Полное приращение ф-и: 
Непр-ть: 
|
|
|
Частные производные 

Производные высших порядков

Утв-е: Смешенные производные по одним и тем же переменным, отличающиеся только порядком дифференцирования равны, если они непрерывны.
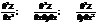
Дифференциал: 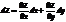
Дата добавления: 2018-05-12; просмотров: 242; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
