Произв. ф-и в точке:определение, геометрич. и механич. смысл. Уравнение касательной.
F’(xo)= 
Определение: производной ф-и в точке, наз.предел отношен. приращения ф-и в приращение аргумента, когда последнее стремится к нулю.
Обозначения: y’, f’(x), 
, 
Если S(t) – закон движения матер. точки
Vср = 
- средн. скорость т. За время 
V(to)= 
- мнгнов. Скорость точки в том времени to – механич. смысл производн.
Производн. ф-и хар-ет скорость изменен. ф-и относит. изменен. аргумента. Если T(t) – температура тела в том врем. t, то Т’(t) означ. скорость нагреван.(если Т’>0) или остыв.(если Т<0)
Если Х(t) – кол-во хим. вещ-ва в том времени, то X’(t) хар-ет скорость химич. реакций. Если X(t) – численность популяц. микробов, то X’(t) хар-ет скорость распространен. болезни.
Геометрический смысл производной: 
, угловой коэфф. секущей АВ; tg 
угловой коэфф. касательной.
Уравнение касательной. y=yo+f’(xo)(x-xo); Если сущ. конечн. произв. ф-и в т. Xo , то ф-я наз. Дифференцируемой в т. Xo
Теорема: ф-я f(x) диф-на в т. Xo , то она непрер. В т. Xo (обратное утверждение, вообще говоря, неверно)
Док-во: Проверим: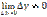 
Основные правила дифференцирования
1). 
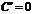
Д-во: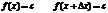 
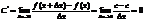
2). 
Д-во: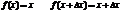 
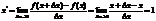
3). 
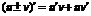
Д-во: 
4). 
Д-во: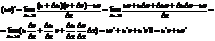 
4’).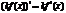 
5). 
Д-во: 
Дифферецирование сложной и обратной функции. Логарифмическое дифференцирование.
1).Производная сложной ф-ии y=f(g(x));
|
|
|
z=g(x) – промежуточный аргумент
f(z) – внешняя ф-я
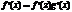- производная сложной ф-ии равна производной внешней ф-ии на
производную промежуточного аргумента
Д-во: 
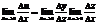
,т.к. z=g(x) – дифф.=> непрерывна
=> 
2).Производная обратной ф-ии y=f(x) – дифф. и x=f -1(y) – обратное тожд. дифф. 
Д-во: 
, т.к. x=f -1(y) – дифф. => непрерывна
Логарифмическое дифференцирование
- сложная показательная
осн. лог. тождество
б)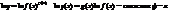 
Вывод таблицы производных: тригонометрические и обратные тригонометрические функции.
1. (sin x)’=cos x
2. (cos x)’= -sin x
3. (tg x)’= 
4. 
5. 
6. 
7. 
8. 
Вывод таблицы производных: логарифмическая, показательная и степенные функции.
логарифмическая
показательная
степенная
Произведение высших порядков, производные функций, заданных неявно и параметрически.
1)Производная высших порядков.
Y ”=(f ’(x))’- Производная второго порядка.
=( 
)
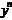Если S(t) закон движения точки, то U(t)=S ’(t) – скорость в момент времени.
U ’(t)=S’’(t)= a(t)- ускорение тела в момент времени.
2)Производная функций заданных неявно
y=f(x)- явно заданная функция.
|
|
|
F(x;y(x))=0 неявно заданная функция Y.
Дифференцируем функцию F(x;y(x)), считая Y сложной функцией.
Выражаем y’ как функцию x и y.
3) Производная функций заданных параметрически.
t- параметр
f(t) и g(t)- дифф. и существует.
я функция.
Дифференциал функции и его применение . Дифференциалы высших порядков.
Утв-е смешанные производные по одним и тем же перемен-х, отличающейся только порядкам дифференц-я, равны, если они непрерывны.
; 
.
Дифференциал: 
.
Пример:
Дифференциалы:
Пример:
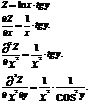
Теорема Ферма
Теорема Ферма: Если f(x) определена на множестве D и в точке х0 €D принимает наибольшее или наименьшее знач., тогда существует f’(x0), то f’(x0)=0 .
Теорема Роля: Функция f(x) непрерывна на отрезке [a,b]и диффер. на множестве(a,b) и f(а)= f(b), тогда сущ. т. С€(a,b) такая, что .
Теорема Лагранжа: Функция f(x) непрерывна на [a,b] и диффер на множестве (a,b), тогда т. С€(a,b), так что – функция Лагранжа f(b)-f(a)=f’(c)*(b-a).
Дата добавления: 2018-05-12; просмотров: 204; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!