Минор и алгебраическое дополнение элемента определителя. Разложение определителя по строке и столбцу.
Высказывания и логические операции над ними.
Высказывание - предложение которое может быть истинным или ложным (логическая переменная)
1.Отрицание (если р высказывание, то р отрицание р)
2.Коньюнкция ( р^q – может быть истинной только в случае, когда оба высказывания истины)
3.Дизъюнкция(pvq – может быть ложной только в одном случае, когда оба высказывания ложны)
4.Имплекция (p→q, ложно только если p-истина q-ложь)
5.Эквиваленция (P↔Q , xor, 0xor0 =1; 1xor1 =1 остальные случаи ложь)
Свойства:
o p^q<=>q^p; pvq<=>qvp; коммутативность
o (p^q)^r<=>p^(q^r); (pvq)vr<=>pv(qvr); ассоциативность
o p^(qvr)<=>(pvq)v(pvr); pv(q^r)<=>(pvq)^(pvr); дистрибутивность
o p<=>p;
o (p^q)<=>pvq ; pvq<=>p^q ; законы Моргана
o (p=>q)<=>(q v p)
o (p=>q)<=>(q=>p)
Высказывания, зависящие от переменной.
p(n): ”n-простое число”
q(x): “x2>5”
r(x;y): “x-y>1”
Пусть высказывание p(x) задано на множестве U.
Множество значений аргумента, при которых высказывание истинно, называется множеством истинности.
Обозначим A и B множеством истинности высказываний p(x) и q(x) соответственно
Логические операции:
1.Отрицание p(x) истинно на A=U A
2.Коньюнкция ( р(x)^q(x) истинна на A∩B
3.Дизъюнкция (p(x)vq(x) истина на AVB
4.Имплекция (p(x)→q(x) истинна на BVA
5.Эквиваленция (p(x)↔q(x) истинно если A=B
Метод математической индукции.
Кванторы:
- квантор общности «для любого»;
- квантор существования «существует»;
Принцип математической индукции:
|
|
|
1. Доказывается истинность p(1) т.е. проверяется, что высказывание истинно n=1
2. Предполагается, что высказывание истинно при n=k, p(k)-истинна. Проверяем истинность высказывания. p(k+1), т.е. при n=k+1. В этом случае выск 
истинно
Бином Ньютона, треугольник Паскаля
Бином Ньютона
Факториал: n!=n(n-1)…2*1
3!=3*2*1=6
0!=1
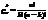- число сочетаний из n элементов по k эл-в
Треугольник Паскаля
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Пр.: 
Комплексные числа и формы их представления.
- (комплексные числа);
i – мнимая единица; 
Z – комплексное число;
;
C = { 
; 
};
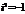y=ReZ – действительная часть числа Z;
x=ImZ – мнимая часть числа Z;
Z=ReZ + 
;
– число, комплексно-сопряжённое к Z = x +i*y.
Формы представления комплексных чисел:
- тригонометрическая форма.
; - показательная форма.
; 
;
; 
;
Арифметические операции:
; 
;
1) Сложение (вычитание);
;
2) Умножение;
;
3) Деление;
;
Формулы Эйлера:
1) 
- результат сложения.
2) 
; - результат вычитания.
|
|
|
Умножение и деление комплексных чисел в тригонометрической форме.
; 
;
А) Умножение:
Б) Деление:
Вывод формулы Муавра.
Док-во по методу мат. индукции:
n=1 
Предположим 
n=k+1
Формулы корней n-ой степени из комплексных чисел.
1. Извлечение корня n-ой степени
;
;
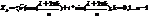
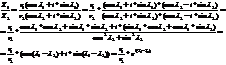
2. Решение уравнений над полем комплексных чисел:
-Z0 – назыв. Корнем многочлена Рn(Z), если Pn(Z0)=0
Утверждение1: Z0 является корнем многочлена Pn(Z) тогда и только тогда когда Pn(Z) без остатка делится на (Z- Z0).
Утверждение2: Любой многочлен Pn(Z) имеет n корней на множестве комплексных чисел и представляются в виде 
Матрицы и операции над ними
Матрица Amxn – это таблица чисел
Amxn = 
Квадратная матрица (An)
A1xn = 
- матрица-строка
Amx1 = 
- матрица-столбец
0mn = 
- нулевая матрица
En = 
- единичная матрица
Операции над матрицами:
Сложение и вычитание:
Amxn 
Bmxn=Cmxn, где cij=aij±bij
i=1, 2, 3–строка, j=1, 2, 3,…,n-столбец.
Свойства этой операции:
1. А+В=В+А – коммутативность;
2. (А+В)+С=А+(В+С) – ассоциативность;
3. А+0=А.
Умножение матрицы на число:
k*A=B, k 
R
b=k*a
Свойства этой операции:
k*(l*A)=(k*l)*A=l*(k*A)– ассоциативность;
(k+l)*A=k*A+l*A– дистрибутивность;
k*(A+B)=k*A+k*B– дистрибутивность;
Умножение матриц:
|
|
|
Amxk*Bkxn=Cmxn
cij=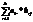 
(i-ая строка первой матрицы умножается на j-ый столбец второй)
Свойства этой операции:
(A*B)*C=A*(B*C)– ассоциативность;
(A+B)*C=A*C+B*C и A*(B+C)=A*B+A*C– дистрибутивность;
A*B 
B*A– вообще говоря;
Amxn*En=Amxn и En*Amxn= Amxn
Транспонирование матриц:
(Amxn)T= 
= Bnxm
Определители и их свойства.
detA – детерминант матрицы А
detA1= 
=a11
detA2= 
=а11*а22-а21*а12
- +
|
|
Доказательство:
=
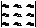=а11*а22*а33+а31*а12*а23+а21*а32*а13-(а31*а22*а13+а21*а12*а33+а11*а21*а23)=
=а11*(а22*а33-а32*а23)-а12*(а21*а33-а31*а23)+а13(а21*а32-а31*а22)=
=а11*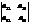 
-а12* 
+а13* 
=
=a11*M11-a12*M12+a13*M13=
=a11*A11-a12*A12+a13*A13 – что и требовалось доказать
Свойства определителя:
При транспонировании матрицы ее определитель не меняется:
det(A)T= detA=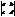 
=a*d-b*c= 
- равноправие строк и столбцов
Если 2 строки (столбца) поменять местами, то определитель поменяет знак:
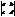=ad-bc=-(bc-ad)=-
Определитель, содержащий нулевую строку (столбец) равен нолю:
=0-0=0
Определитель, содержащий одинаковые строки (столбцы) равен нолю:
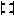=a*c-a*c=0
|
|
|
Общий множитель какой либо строки (столбца) можно вынести за знак определителя:
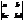=k*a*d-k*b*c=k*(ad-bc)=k
Определитель, содержащий пропорциональные сроки (столбцы) равен нолю:
=k*a*b-k*a*b=0
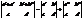
Орпеделитель не изменится, если к элементу какой-либо строки (столбца) прибавить элемент другой сторки (столбца), умноженные на какое-либо число:
det (An*Bn)= det An* det Bn
Минор и алгебраическое дополнение элемента определителя. Разложение определителя по строке и столбцу.
Минором Mijэлемента aij пределителя n-го порядка называют определитель (n-1)-го порядка, который получается из исходного вычёркиванием i-й строки и j-го столбца.
Алгебраическое дополнение Aij элемента aij определителя находится по формуле:
Теорема 1
Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
det 
-- разложение определителя по i-той строке
det 
--разложение определителя по j-тому столбцу
Доказательство
Теорема 2
Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равен нулю.
если 
Замечание
Определители 4-го и более высокого порядков вычисляется разложением по строке или столбцу.
Дата добавления: 2018-05-12; просмотров: 268; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!