Обратная матрица: определение, построение и свойства. Решение матричных уравнений.
Если определитель матрицы А не равен нулю, то матрица А является невырожденной, а если определитель матрицы равен нулю, то матрица А является вырожденной.
Матрица, состоящая из алгебраических дополнений к элементам матрицы А, наз. Взаимной.
к матрице А
Матрица A-1называется обратной к матрице А, если: A*A-1=a-1*A=E
Лемма: 
Проверка:
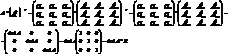
Теорема 1
Для того, чтобы у матрицы А существовала обратная матрица 
, необходимо и достаточно, чтобы матрица А была невырожденной.
Доказательство
, то по лемме 
Теорема 2
Если 
, то она единственна.
Доказательство (от противного)
Пусть 
- обратные к матрице А
Свойства:
1. 
2. 
3. 
4. 
Матричные уравнения:
1. А*Х=В
2. Х*А=В
Х*А* 
Системы линейных уравнений. Совместные и эквивалентные системы. Элементарные преобразования системы.
(*)
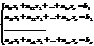
A X B
A*X=B,где A= 
-матрица коэффициентов системы
-столбец неизвестной 
-столбец сводных членов системы
Совокупность чисел
X1=C1, X2=С2,Xn=Cn, , …- называется решением системы(*),если при подстановке их в уравнение обращает их в тождество.
Совместная система- система, которая имеет хотя бы одно решение.
Определённая система-система, которая имеет единственное решение.
Две системы называются эквивалентными, если их множество решений совпадают.
Элементарные преобразования системы:
1)перестановка строк;
2)умножение строки на число 
;
3)прибавление к строке другой строки умноженной на число.
|
|
|
Утверждение: элементарные преобразования приводят систему к эквивалентной.
Решение систем с невырожденной матрицей матричным методом и с помощью формул Крамера.
Существует три метода решения систем с невырожденной матрицей:
1)матричный
2)формулы Крамера
3)метод Гаусса
Матричный способ:
A*X=B(*)
Формулы Крамера:
где 
; 
; 
-Формулы Крамера
Метод Гаусса (исключения неизвестных)
Составляем расширенную матрицу системы(А/B):
(A|B)= 
Обратный ход матрицы Гаусса:
Ранг и базисный минор.
Опр.1 На пересечении ķ строк и ķ столбцов образуется матрица ķ-ого порядка. Её
определитель называется минором ķ-ого порядка.
Опр.2 Рангом матрицы называется – наибольший порядок ненулевых миноров.
Опр.3 Любой ненулевой минор, порядок которого равен рангу наз. – базисным. Его строки и столбцы называются базисными.
Свойства ķ(А):
ķ(Аmxn) 
min(m;n)
ķ(A)=0 
A=0
ķ(An)=n detAn 
(максимальный) ( базисный минор)
Утверждение. Элементарное преобразование не изменяет ранг матрицы (не влияет на равенство 0(нулю)).
Линейная зависимость и независимость элементов. Теорема о базисном миноре.
|
|
|
Совок-ть элементов 
(столбцы)
Линейная комбинация элементов ei : определяется их суммой с каким-либо коэффициентом.
, причем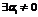 
Совокупность элементов 
называется линейно зависимой, если хотя бы один из них является линейной комбинацией остальных.
Составляем равенство
=0
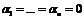
Линейная независимость Линейная зависимость
Теорема о базисном миноре:
Любая небазисная строка(столбец) матрицы является линейной комбинацией базисных.
Базисные строки (столбцы) линейно независимы.
Следствие: наибольшее число линейно-независимых строк(столбцов)матрицы равно рангу.
Дата добавления: 2018-05-12; просмотров: 197; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!