Оценка коэффициентов парной регрессии на компьютере
Для решения задачи прогнозирования требуется по экспериментальным точкам провести гладкую кривую (или, в общем случае, многомерную поверхность), то есть выявить функциональную зависимость (аппроксимация), продлить ее в неизученную область (экстраполяция) и оценить надежность прогноза.
Для конкретизации задачи будем исследовать продажу мороженого в зависимости от температуры воздуха в диапазоне 0О – 30О: Постановка задачи: по имеющимся данным о продажах в диапазоне температур 0О…20О спрогнозировать уровень и диапазон продаж при температуре 30О. Обобщённая модель:
y = f (x )+u
где x– независимая (экзогенная) переменная: температура,
y - зависимая (эндогенная) переменная: продажа мороженого.
В таблице 4.1 и на рисунке 4.1 приведены известные нам объемы продаж при различных температурах в диапазоне 0О – 20О, требуется дать прогноз на диапазон 21О – 30О. Рассмотрим две модели и 4 способа решения задачи.
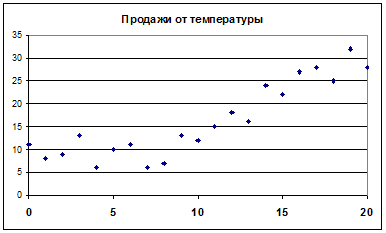Таблица 4.1
| Температура X | Продажи Y |
| 0 | 11 |
| 1 | 8 |
| 2 | 9 |
| 3 | 13 |
| 4 | 6 |
| 5 | 10 |
| 6 | 11 |
| 7 | 6 |
| 8 | 7 |
| 9 | 13 |
| 10 | 12 |
| 11 | 15 |
| 12 | 18 |
| 13 | 16 |
| 14 | 24 |
| 15 | 22 |
| 16 | 27 |
| 17 | 28 |
| 18 | 25 |
| 19 | 32 |
| 20 | 28 |
Рис.4.1.
Рис.4.1.
В данной задаче температуры упорядочены изначально. В противном случае обычно требуется провести предварительную сортировку данных по независимой (экзогенной) переменной: выделить таблицу, в меню Данные – Сортировка – указать столбец независимой переменной – ОК.
|
|
|
4.1. Построение диаграмм и спецификация моделей.
Решение эконометрической задачи начинается со спецификации модели, то есть выявления функции регрессии и особенностей возмущений. Для этого надо построить диаграмму: выделить оба столбца данных и построить диаграмму Точечная, что позволит сразу правильно расположить данные по оси абсцисс и оценить корреляцию X и Y или ее отсутствие. Диаграмма позволяет оценить вид аппроксимирующей функции, может быть, различной в разных диапазонах Х, и увидеть точки, выпадающие из закономерности. Эти точки надо удалить из выборки и рассматривать отдельно. В данном примере аномальные значения Y могут быть связаны с праздничными днями и премиями.
Если функция Ŷ = f(X) нелинейная, то ее, как правило, надо линеаризовать, заменив значения Xи Yна их логарифмы, квадраты, квадратные корни или более сложные функции, а после решения задачи провести обратное преобразование полученной аппроксимирующей функции. Если точки уплотняются в левой части диаграммы, то целесообразно заменить значения Х, а может и Y их логарифмами. Целесообразно построить гистограммы частотных распределений X и Y, и при распределении с “толстым хвостом” провести логарифмирование.
|
|
|
В данном случае можно увидеть на диаграмме, что от 0о до 10о продажи не возрастают, а после 10о – возрастают. Можно построить две модели с расчетом коэффициентов по различным диапазонам:
1) Линейная Y = a + b X + u в диапазоне от 10о до 20о;
2) Парабола Y = a + b X + с Х2 + u в диапазоне от 0о до 20о.
(Любую функцию в некотором диапазоне можно достаточно точно представить многочленом).
В первом случае мы отбрасываем половину исходных данных и считаем, что до 10оодна закономерность, а свыше 10о – другая. Во втором случае мы используем для настройки модели все данные. Выбор модели зависит от теоретических закономерностей и от личного опыта, а также от результатов эконометрических тестов, например, теста Чоу.
Параметры моделей и прогноз можно получить, построив диаграммы.
Модель1:
- выделите оба столбца в диапазоне температур 10о – 20о, постройте диаграмму типа Точечная;
- щелкните правой клавишей мыши по любой точке, в появившемся окне щёлкните Добавить линию тренда, установите Тип – Линейная, выберите Параметры, установите Прогноз вперед на 10 единиц и флажки Показывать уравнение на диаграмме, Поместить на диаграмму величину достоверности (R^2) – ОК. На диаграмме появятся уравнение регрессии и коэффициент детерминации.
|
|
|
Модель 2:
- выделите оба столбца в диапазоне температур 0о – 20о, постройте диаграмму типа Точечная;
- щелкните правой клавишей мыши по любой точке, в появившемся окне щёлкните Добавить линию тренда, установите Тип – Полиномиальная, Степень 2, выберите Параметры, установите Прогноз вперед на 10 единиц и флажки Показывать уравнение на диаграмме, Поместить на диаграмму величину достоверности (R^2) – ОК.
Рис.4.1. Диаграммы линейной и параболической моделей.
Индекс детерминации R2 даёт представление о надёжности модели. Критерии качества модели и её параметров мы обсудим позднее.
Возможно использование других функций: степенной, экспоненты, логарифма. Обратите внимание, что модели дают различные прогнозы на 30о.
Данный пример служит иллюстрацией того, что в разных диапазонах переменных могут действовать разные закономерности. Из житейских соображений следует, что параболу нельзя продлевать в область отрицательных значений температуры: продажи мороженого зимой не вырастут. Обе функции нельзя экстраполировать на 40 и более градусов. Для каждой закономерности существует диапазон значений, или область определения экзогенной переменной.
|
|
|
Возникает вопрос: можно ли повысить качество модели, увеличив степень полинома? Это возможно, но только при очень большом количестве измерений и высоком (>0,95) коэффициенте детерминации. Попробуем увеличить степень полинома в нашем примере до 4, а последние 4 замера (17о - 20о) используем не для настройки модели, а для проверки её адекватности. Получим результат: Рисунок 4.2А. Получился высокий R2, последние 4 значения Yпредсказаны неплохо. Решим, что модель качественная и адекватная, используем её для прогнозирования. Получим абсолютно безобразный прогноз: Рисунок 4.2 Б.
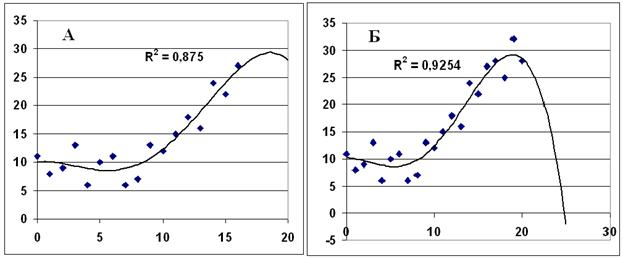Рис. 4.2.
Это произошло из-за большого количества тесно связанных влияющих переменных – х в различных степенях, что привело к высокой дисперсии (большим ошибкам) коэффициентов. В диапазоне настройки эти ошибки друг друга компенсируют, а в области прогноза – нет.
Функция ЛИНЕЙН
Параметры линейной регрессии можно определить с помощью встроенной статистической функции ЛИНЕЙН. Порядок вычисления следующий:
- Ввод исходных данных;
- Выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1х2 – для получения только оценок коэффициентов регрессии;
- Активизируйте Мастер функций – щелкните fx на панели инструментов или в главном меню выберите Вставка – Функция;
- В окне Категория выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните ОК.
- Заполните аргументы функции:
q Известные значения у – диапазон, содержащий данные результативного признака;
q Известные значения_х – диапазон, содержащий данные факторов независимого признака;
q Константа – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении: если Константа = 1, то свободный член рассчитывается обычным способом, если Константа = 0, то свободный член равен 0;
q Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу ( = 1) или нет (=0);
q Нажмите комбинацию клавиш CTRL – SHIFT – ENTER. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей таблице:
Таблица 4.2.
| Коэффициент b | Коэффициент a |
| Среднеквадратическое отклонение b | Среднеквадратическое отклонение a |
| Индекс детерминации R2 | Среднеквадратическое отклонение остатков |
| F – статистика | Число степеней свободы остатков |
| Регрессионная сумма квадратов S(Ŷ - Ŷсредн.)2 | Сумма квадратов остатков S(Y - Ŷ )2 |
Полученный результат:
| 1,7818 | -4,2727 |
| 0,2451 | 3,7578 |
| 0,8544 | 2,5710 |
| 52,833 | 9 |
| 349,23 | 59,490 |
Если случайно щёлкнули ОК, нажмите на клавишу F2, а затем – на комбинацию клавиш CTRL – SHIFT – ENTER.
Для вычисления параметров показательной функции Y = abxв Excel применяется встроенная статистическая функция ЛГФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.
Как видите, полученные коэффициенты a, b и индекс детерминации R2 совпадают с результатами их оценки с помощью диаграммы. Кроме того, получены погрешности коэффициентов a, b, стандартное отклонение Y, число степеней свободы остатков (n-2 = 9), сумма квадратов остатков, регрессионная сумма квадратов = S ( Ŷ - Ŷсредн.)2 и статистика Фишера.
4.3. Сервис Регрессия
Ещё больше информации даёт сервис Регрессия из Пакета анализа Excel. Для его запуска надо щелкнуть в Меню Excel 2003 и более ранних версий Сервис – Анализ данных – Регрессия. (Если Анализ данных в меню Сервиса не появится, щелкните Надстройки и установите флажок Пакет анализа). В Excel 2007 и 2010 Пакет анализа вызывается в разделе Меню Данные. Если Анализ данных не виден, установить его: Файл – Параметры – Надстройки – Параметры Excel применить – Пакет анализа. Укажите диапазоны ячеек Y и X и на какой лист выводить результаты – на новый или на тот же. В этом случае надо указать достаточно большой диапазон ячеек для вывода. Поставьте флажок Метка, если выделили X и Y с заголовками.
Сервис Регрессия выводит все статистические характеристики модели с соответствующими надписями. Сервис Регрессия может применяться для линейных или линеаризованных моделей.
Оценка параметров Модели 1 с использованием сервиса Регрессия:
Таблица 4.3.
| Регрессионная статистика |
| |
| Множественный R | 0,9243 | Квадратный корень из коэффициента детерминации. Для линейной модели – коэффициент корреляции |
| R-квадрат | 0,8544 | Коэффициент детерминации |
| Нормированный R-квадрат | 0,8382 |
|
| Стандартная ошибка | 2,5710 | Стандартное отклонение остатков |
| Наблюдения | 11 | Количество наблюдений n |
| Дисперсионный анализ | Число степеней свободы сумм | Суммы квадратов | Дисперсия на одну степень свободы |
|
|
| df | SS | MS | F | Значимость F | |
| Регрессия (Y^) | 1 | 349,23 | (349,23/1=) 349,23 | 52,83 | 4,72E-05 |
| Остаток | 9 | 59,490 | (59,49 / 9=) 6,610 |
|
|
| Итого (Y) | 10 | 408,72 | (Var(Y) =) 40,87 |
|
|
|
|
|
|
|
|
|
|
| Коэффи-циенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -4,2727 | 3,7578 | -1,1370 | 0,2849 | -12,773 | 4,228 |
| X | 1,7818 | 0,2451 | 7,2686 | 4,72051E-05 | 1,227 | 2,336 |
Стандартные надписи и дополнительные пояснения позволяют быстро разобраться в таблице результатов сервиса Регрессия. Коэффициент детерминации (здесь R-квадрат), статистика Фишера F и t-статистика Стьюдента разобраны в разделах 2.3 и 3.2. Осталось добавить про Значимость F и Р-Значение. Соответствующие числа в таблице означают вероятности принятия неверных гипотез относительно наличия влияния всех переменных на Y (Значимость F) и каждой экзогенной переменной в отдельности (Р-Значение). В данном случае имеется одна влияющая переменная, поэтому значимости F и b совпадают. Погрешность b равна 14%, t-статистика b высокая, вероятность того, что b £ 0, то есть продажи не зависят от температуры, ничтожно мала (P-Значение = 4,72051E-05). Погрешность a равна 88%, t-статистика низкая, и вероятность того, что a окажется больше нуля, равна 28,5% (Р-значение). В разделе Дисперсионный анализ выведены: регрессионная сумма квадратов S( Ŷ - Ŷсредн.)2 , здесь равная 349,23 , и соответствующая дисперсия для одной степени свободы (один х), а также сумма квадратов остатков, здесь 59,49 , дисперсия остатков 6,61 и соответствующие величины для эндогенной переменной Y.
Сервис Регрессия можно применять к линеаризованным моделям, а также считая х в разных степенях в полиноме как самостоятельные экзогенные переменные, то есть сводя полиномиальную модель к модели множественной регрессии, которая рассмотрена далее. Пример: оценка параметров Модели 2 (парабола) с помощью сервиса Регрессия:
Таблица 4.4.
|
| Темпера-тура | Продажи | ВЫВОД ИТОГОВ |
|
|
|
|
| x^2 | x | y |
|
|
|
|
|
| 0 | 0 | 11 | Регрессионная статистика |
|
|
| |
| 1 | 1 | 8 | Множественный R | 0,940 |
|
|
|
| 4 | 2 | 9 | R-квадрат | 0,884 |
|
|
|
| 9 | 3 | 13 | Нормированный R-квадрат | 0,871 |
|
|
|
| 16 | 4 | 6 | Стандартная ошибка | 2,961 |
|
|
|
| 25 | 5 | 10 | Наблюдения | 21 |
|
|
|
| 36 | 6 | 11 |
|
|
|
|
|
| 49 | 7 | 6 | Дисперсионный анализ |
|
|
|
|
| 64 | 8 | 7 | df | SS | MS | F | |
| 81 | 9 | 13 | Регрессия | 2 | 1205 | 602 | 68,7 |
| 100 | 10 | 12 | Остаток | 18 | 157,8 | 8,7 |
|
| 121 | 11 | 15 | Итого | 20 | 1363 |
|
|
| 144 | 12 | 18 |
|
|
|
|
|
| 169 | 13 | 16 |
|
|
|
|
|
| .... | .... | .... |
|
|
|
|
|
| 361 | 19 | 32 |
|
|
|
|
|
| 400 | 20 | 28 |
|
|
|
|
|
| Коэффици- енты | СKO | t | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 9,1942 | 1,7674 | 5,2020 | 0,0001 | 5,48 | 12,90 |
| x^2 | 0,0756 | 0,0198 | 3,8235 | 0,0012 | 0,034 | 0,117 |
| x | -0,3287 | 0,4095 | -0,8025 | 0,4327 | -1,189 | 0,531 |
4.4. Сервис Поиск решения (Solver)
Использование сервиса Поиск решения позволяет наглядно продемонстрировать суть метода наименьших квадратов (МНК). Вызывается он так же, как и Анализ данных: в Excel-2003 и более ранних версиях через меню Сервис (если не вызывается, то Сервис-Надстройки) ; в Excel-2007 и 2010 в меню Данные (если не вызывается, то Пуск – Параметры Excel – Надстройки – Перейти). Схема расчетов та же, что и в задачах математического программирования:
- задать произвольные коэффициенты аппроксимирующей функции f(X) ,
- построить функцию Ŷ = f(X) в заданном диапазоне Х,
- вычислить отклонения Y – Ŷ для диапазона, в котором значения Yиспользуются для настройки модели, то есть оценки коэффициентов,
- вычислить все (Y – Ŷ )2 и их сумму S(Y – Ŷ )2 (сумма квадратов отклонений (остатков) ,
- вызвать Поиск решения, целевая ячейка S(Y – Ŷ)2, Изменяя ячейки коэффициенты, ограничений нет, Выполнить.
Применение Поиска решения к линейной модели, представлена в таблице 4.5.
Метод наименьших квадратов с Поиском решения может применяться для настройки нелинейных моделей. Его использование для настройки Модели 2 – параболической – показано в Таблице 4.6.
Показатель качества линейной модели – коэффициент корреляции Х и Y Rxy и его квадрат – коэффициент детерминации R2.
Вычисленные для обеих моделей R2, DW, GQ представлены в таблицах, а также показаны графики остатков. Видно, что качество обеих моделей высокое, применение МНК правомерно. Применение для прогноза одной из двух моделей зависит от дополнительной информации и личного опыта.
Вычисление эластичности
Важная характеристика экономических процессов – эластичность, которая показывает, на сколько процентов изменится зависимая переменная Y при увеличении влияющей переменной Хна 1 % :
Э = (ΔY / Y) / (ΔX / X)
Применение компьютера позволяет вычислить эластичность по всему диапазону Х, а не только средние значения, как при ручном счете.
В качестве Х иY берутся их средние значения на соответствующих интервалах ΔX иΔY, расчет ведется по аппроксимирующей функции Ŷ:
Э= (Ŷ1 – Ŷ0)/( Ŷ1+ Ŷ0)/(Х1 – Х0)*(Х1+Х0)
где индексы 0 и 1 относятся к первым двум значениям переменных Хи Ŷ. Затем формула копируется на весь диапазон, кроме последней ячейки; в Модели1 расчет начинается с температуры 10о. Графики показывают, что расчет эластичности по разным моделям приводит к различным результатам. Обычно экономисты используют среднюю эластичность
,
Где DY/ DX – средний наклон функции Ŷ = f(X). Применение функции эластичности позволяет изучать влияние добавок Х на изменение Y при различных значениях влияющей переменной.
Далее представлены результаты расчетов по двум моделям.
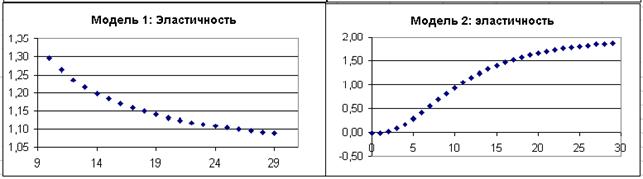Рис.4.3.
Таблица 4.5.
| Модель 1 | a | b | |||
| -4,2727 | 1,7818 | ||||
| Температура X | Продажи Y | Ŷ. | Остатки: Y-Ŷ | (Y-Ŷ)2 | Эластичность |
| 10 | 12 | 13,55 | -1,55 | 2,39 | 1,30 |
| 11 | 15 | 15,33 | -0,33 | 0,11 | 1,26 |
| 12 | 18 | 17,11 | 0,89 | 0,79 | 1,24 |
| 13 | 16 | 18,89 | -2,89 | 8,36 | 1,22 |
| 14 | 24 | 20,67 | 3,33 | 11,07 | 1,20 |
| 15 | 22 | 22,45 | -0,45 | 0,21 | 1,18 |
| 16 | 27 | 24,24 | 2,76 | 7,64 | 1,17 |
| 17 | 28 | 26,02 | 1,98 | 3,93 | 1,16 |
| 18 | 25 | 27,80 | -2,80 | 7,84 | 1,15 |
| 19 | 32 | 29,58 | 2,42 | 5,85 | 1,14 |
| 20 | 28 | 31,36 | -3,36 | 11,31 | 1,13 |
| 21 | 33,15 | 1,13 | |||
| 22 | 34,93 | Sост2 | 59,49 | 1,12 | |
| 23 | 36,71 | Корреляция | 0,92 | 1,11 | |
| 24 | 38,49 | Индекс детерминации | 0,85 | 1,11 | |
| 25 | 40,27 | 1,10 | |||
| 26 | 42,05 | Автокор-реляция | -0,58 | 1,10 | |
| 27 | 43,84 | DW | 3,17 | 1,10 | |
| 28 | 45,62 | GQ | 1,61 | 1,09 | |
| 29 | 47,40 | Дисп.ост.1 | 4,55 | 1,09 | |
| 30 | 49,18 | Дисп.ост.2 | 7,34 | ||
| ДИСП Y | ДИСП Ŷ | ДИСП остатков | |||
| 40,87 | 34,90 | 5,95 |
Таблица 4.6.
| Модель 2 | a | b | c | ||
| 9,1942 | -0,3286 | 0,075588 | |||
| Температура X | Продажи Y | Ŷ | Остатки: Y-Ŷ | (Y-Ŷ)2 | Эластичность |
| 0 | 11 | 9,19 | 1,81 | 3,26 | -0,01 |
| 1 | 8 | 8,94 | -0,94 | 0,89 | -0,02 |
| 2 | 9 | 8,84 | 0,16 | 0,03 | 0,01 |
| 3 | 13 | 8,89 | 4,11 | 16,90 | 0,08 |
| .... | .... | .... | .... | .... | .... |
| 18 | 25 | 27,77 | -2,77 | 7,67 | 1,57 |
| 19 | 32 | 30,24 | 1,76 | 3,10 | 1,62 |
| 20 | 28 | 32,86 | -4,86 | 23,59 | 1,66 |
| 21 | 35,63 | 1,69 | |||
| 22 | 38,55 | 1,72 | |||
| 23 | 41,62 | Sост2 | 157,82 | 1,75 | |
| 24 | 44,85 | Индекс детерминации | 0,88 | 1,78 | |
| 25 | 48,22 | F | 61,0 | 1,80 | |
| 26 | 51,75 | Автокор-реляция | -0,13 | 1,82 | |
| 27 | 55,43 | DW | 2,26 | 1,84 | |
| 28 | 59,25 | GQ | 1,05 | 1,85 | |
| 29 | 63,23 | Дисп.ост.1 | 7,86 | 1,87 | |
| 30 | 67,37 | Дисп.ост.2 | 8,28 | ||
| ДИСП Y | ДИСП Ŷ | ДИСП остатков | |||
| 68,19 | 60,31 | 7,89 |
Некоторые комментарии к таблицам.
Индексы детерминации и F-статистики вычислены по формулам ( 3.2 ) и (3.3) на стр. 29 с использованием функции ДИСП. Коэффициент автокорреляции остатков Rавт вычислен с помощью функции КОРРЕЛ(е1:еn-1 ; е2:еn), то есть в первом окне указан диапазон остатков с первого до (n-1)-го, во втором – со второго до n-го. Тест Дарбина-Уотсона осуществлён по формуле
DW=2(1–Rавт). В линейной модели DW=3,17 , то есть попадает в интервал 3,07…4, соответствующий отрицательной автокорреляции. Этот пример объясняет секрет процветания казино. Исходные данные для этой задачи автор придумал сам, и тест Дарбина-Уотсона выявил, что эти числа не являются случайными. Человек не может создать абсолютно случайный ряд чисел, а рулетка его создаёт. Из теории игр следует, что отклонение от оптимальной смешанной стратегии, в данном случае ряда случайных чисел, приводит к проигрышу игрока и выигрышу казино.
Тест Голдфелда-Квандта GQ проведён по первой и второй половинам диапазона остатков: данных слишком мало, чтобы исключать середину, как положено по правилам.
Нелинейные модели
Довольно часто приходится использовать нелинейные функции регрессии двух видов:
1. Регрессии, нелинейные относительно включённых в анализ объясняющих переменных:
Полином второй, редко третьей степени y = a + bx+сх2+u.
Гипербола y = a +b/x +u.
Эти модели сводятся к линейным заменой переменных: z = х2 для полинома и z=1/x для гиперболы. После этого можно использовать функцию ЛИНЕЙН и сервис Регрессия, выделяя в качестве влияющих переменных х и z для полинома и z для гиперболы.
2. Регрессии, нелинейные по оцениваемым параметрам относятся:
Степенная y = axbe;
Показательная y = abxe;
Экспоненциальная y = ea+bxe.
Здесь e =1+ u. Эти модели могут быть линеаризованы логарифмированием, после чего можно использовать функцию ЛИНЕЙН и сервис Регрессия. Например, показательная функция преобразуется в ln(y) =ln(a) +xln(b)+ln(e), или, после переименования z=A+cx+v.
После нахождения коэффициентов A и c можно вычислить z^=A+cx и y^=exp(z^).
Самостоятельная работа
По данным Таблицы 4.7 определите по графику вид каждой функции регрессии, оцените её коэффициенты, используя ЛИНЕЙН или Регрессия с линеаризацией, или Поиск решения. По вектору остатков вычислите R2, F, GQ,DW. Сделайте выводы о качестве модели.
Таблица 4.7.
| x | y | y | y | y | y | y | y | y | y | y | y | y | y | y |
| 1 | 55 | 3 | 55 | 1 | 88 | 4 | 9 | 55 | 177 | 33 | 2 | 45 | 444 | 144 |
| 2 | 50 | 5 | 55 | 3 | 77 | 5 | 6 | 66 | 88 | 22 | 4 | 65 | 222 | 133 |
| 3 | 40 | 9 | 55 | 6 | 66 | 12 | 4 | 44 | 88 | 8 | 7 | 47 | 100 | 122 |
| 4 | 22 | 9 | 66 | 11 | 44 | 22 | 9 | 99 | 77 | 7 | 7 | 99 | 88 | 99 |
| 5 | 12 | 22 | 33 | 19 | 33 | 25 | 12 | 122 | 55 | 5 | 9 | 124 | 77 | 99 |
| 6 | 33 | 44 | 33 | 22 | 22 | 17 | 11 | 111 | 66 | 6 | 9 | 117 | 66 | 122 |
| 7 | 38 | 33 | 22 | 11 | 25 | 17 | 18 | 188 | 33 | 3 | 8 | 188 | 55 | 133 |
| 8 | 55 | 77 | 11 | 6 | 16 | 12 | 22 | 222 | 28 | 2 | 5 | 229 | 54 | 144 |
| 9 | 77 | 99 | 11 | 2 | 15 | 4 | 27 | 277 | 27 | 3 | 5 | 366 | 48 | 166 |
| 10 | 77 | 222 | 1 | 2 | 15 | 5 | 27 | 555 | 27 | 2 | 2 | 555 | 47 | 188 |
| x | y | x | y | x | y | x | y | x | y | x | y | x | y | |
| 55 | 3 | 55 | 1 | 66 | 4 | 9 | 55 | 111 | 33 | 1 | 45 | 220 | 55 | |
| 50 | 5 | 50 | 3 | 55 | 5 | 6 | 66 | 88 | 22 | 4 | 228 | 170 | 62 | |
| 40 | 9 | 40 | 6 | 66 | 12 | 4 | 44 | 88 | 8 | 9 | 47 | 100 | 122 | |
| 22 | 9 | 22 | 11 | 44 | 22 | 9 | 99 | 77 | 7 | 7 | 99 | 88 | 99 | |
| 12 | 22 | 12 | 19 | 33 | 25 | 12 | 122 | 55 | 5 | 9 | 124 | 77 | 99 | |
| 33 | 44 | 33 | 22 | 22 | 17 | 11 | 111 | 66 | 6 | 9 | 117 | 66 | 122 | |
| 38 | 33 | 38 | 11 | 25 | 17 | 18 | 188 | 33 | 3 | 8 | 188 | 55 | 133 | |
| 55 | 77 | 55 | 6 | 16 | 12 | 22 | 222 | 28 | 2 | 5 | 229 | 54 | 144 | |
| 77 | 99 | 77 | 2 | 15 | 4 | 27 | 277 | 27 | 3 | 5 | 298 | 48 | 166 |
Контрольные вопросы
1. Метод наименьших квадратов (МНК) и работа с функцией ЛИНЕЙН.
2. Метод наименьших квадратов (МНК) и смысл выходной статистической информации сервиса Регрессия
3. Метод наименьших квадратов (МНК) и его реализация с использованием сервиса “Поиск решения”
4. Оценка погрешности прогноза и проверка адекватности модели
5. Экономический смысл коэффициентов линейного и степенного уравнений регрессии .
Дата добавления: 2018-05-12; просмотров: 276; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!