Взаимосвязь случайных величин

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

Одна из основных задач эконометрики – выявление взаимосвязи переменных. Количественными оценками взаимосвязи служат ковариация и коэффициент корреляции. Ковариация переменных x и y – это ожидаемое значение произведения их отклонений от ожидаемых значений:

сov(x,y) = E((х-E(х))*(y-E(y)))

Для оценки ковариации по выборке используется формула, аналогичная формуле дисперсии

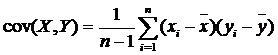
Cov(x,x) – это дисперсия x. Коэффициент корреляции – это ковариация, нормированная на стандартные отклонения x и y:

Коэффициент корреляции – безразмерная величина, изменяется от –1 до +1; близость к нулю означает отсутствие связи переменных.

Практическое задание

Проведите обработку простого массива данных X и Y. Вычислите количество данных, используя функцию Excel СЧЁТ(). До 11 мы считать умеем, но реальные таблицы экономических данных могут быть огромными. Вычислите суммы X и Y, используя функцию S, и их средние значения, используя формулу и функцию СРЗНАЧ(). Вычислите квадраты отклонений X и Y от их средних значений, просуммируйте. Обратите внимание на фиксацию адресов Xcp и Ycp знаком $. Вычислите дисперсии и среднеквадратические отклонения (СКО) по формулам и через функции ДИСП и СТАНДОТКЛОН. Сравните результаты. Вычислите ковариацию и корреляцию по формулам и через функции КОВАР и КОРРЕЛ.

                                                                                      Таблица 2.1

X Y
(X-$Xcp)^2

(Y-$Ycp)^2

(X-$Xcp)*(Y-$Ycp)

10 12
25

109,2

52,2

11 15
16

55,5

29,8

12 18
9

19,8

13,3

13 16
4

41,6

12,9

14 24
1

2,38

-1,54

15 22
0

0,20

0

16 27
1

20,6

4,54

17 28
4

30,7

11,0

18 25
9

6,47

7,63

19 32
16

91,1

38,1

20 28
25

30,7

27,7

11

11

165

247

110

408,7

196

15

22,45

15

22,45

Ковариация

Sum(X-$Xcp)^2 /(N-1)

11

40,8

19,6

КОРЕНЬ

3,31

6,39

СТАНДОТКЛОН

3,31

6,39

Корреляция

Cov/Sx/Sy

0,924

КОРРЕЛ()

0,924

Контрольные вопросы

1. Дифференциальный и интегральный закон распределения случайной величины, виды функций распределения. Что такое “толстые хвосты”?

2. Параметры случайной величины: ожидаемое значение, дисперсия и среднее квадратическое отклонение, коэффициенты ковариации и корреляции.

3. Проверка статистических гипотез, t-статистика Стьюдента, доверительная вероятность и доверительный интервал, критические значения статистики Стьюдента.

Регрессионный анализ

Понятие ожидаемого значения случайной переменной позволяет дать точное определение понятия функции регрессии. Пусть случайная переменная у принимает свои значения в опыте вместе с переменной х (случайной или детерминированной — неважно).

Простая (парная) регрессия представляет собой модель, где ожидаемое значение зависимой (объясняемой, эндогенной) переменной y рассматривается как функция одной объясняющей (независимой или управляемой, предопределённой) переменной х, то есть модель вида

Е(y) =f(x)

Множественная регрессия представляет собой модель, где ожидаемое значение зависимой переменной y рассматривается как функция многих объясняющих переменных, то есть модель вида

Е(y) =f(x₁, х₂, …, x_n)

Случайную переменную у формируют функция f(x) и случайная величина u (uncertainty, disturbance term, возмущение) с ожидаемым значением, равным нулю:

у = f(x) + и

Такое разложение случайной переменной у именуется регрессионным анализом переменной у.

Предполагается, что f(x) отражает идеальную закономерность, на которую накладываются неучтённые факторы или ошибки измерения. В физике это так, а в экономике – нет. В физике параметрами функции f(x) являются константы, которые надо оценить по результатам измерений (скорость света, масса протона, период полураспада радиоактивного изотопа). В экономике измеряемые величины (ВВП, количество населения) и их взаимосвязи постоянно меняются, поэтому нет фундаментальных констант. Тем не менее, эконометрика переняла математический аппарат, разработанный для физики, и мы его будем использовать.

    Регрессионные модели, которые наиболее часто используются в эконометрике:

1) Линейная y = a + bx+u; употребляется наиболее часто, остальные функции стараются преобразовать к линейному виду, линеаризовать.

Регрессии, нелинейные относительно включённых в анализ объясняющих переменных:

2) Полином второй, редко третьей степени y = a + bx+сх²+u.

3) Равносторонняя гипербола y = a +b/x +u.

Эти модели сводятся к линейным заменой переменных: z = х² для полинома и   z=1/x для гиперболы.

К нелинейным регрессиям по оцениваемым параметрам относятся:

4) Степенная y = ax^be;

5) Показательная y = ab^xe;

6) Экспоненциальная y = e^a⁺^bxe.

Здесь e =1+ u. Эти модели могут быть линеаризованы логарифмированием.

    Следует отметить разницу между идеальной закономерностью, которую для линейной модели обычно записывают

y = a + bx+u

и оценённой регрессионной моделью

y = a +bx + e,

а также возмущением u и отклонением, или ошибкой е. Предполагается, что a и b являются реальными константами, а a и bслужат их оценками. В экономике констант нет, но математический аппарат сохраняется. Возмущение u – это отклонение реального замера от идеальной закономерности a+bх, которую мы не знаем. Значит, u мы тоже не знаем, но можем делать предположение о его свойствах. Ошибка е – это разность между реальным у и его значением, оценённым по формуле a + bx; она служит оценкой u.

Коэффициенты b и a можно вычислить по формулам

Метод наименьших квадратов

Для оценки параметров линейной или линеаризованной модели применяется метод наименьших квадратов (МНК). Суть метода состоит в следующем: к реальным данным подбирается функция и её параметры, чтобы разности (отклонения, остатки) между реальными и вычисленными значениями у были минимальны. Но разностей много, поэтому минимизируется сумма квадратов этих разностей:

           Рис.3.1. Отклонения реальных у от оценённой функции регрессии.

Как правило, вычисления проводятся на компьютере с использованием различных сервисов и программ. Далее мы рассмотрим технологию МНК, которую использовали при ручном вычислении параметров парной линейной регрессии.

Сумма квадратов остатков, зависящая от параметров a и b

где n – количество измерений. Эта функция достигает минимума в точке, где её частные производные по a и по b равны нулю:

    или

                                     an + bSx = Sy

                                     aSx + bSx²=Sxy

Это называется система нормальных уравнений. В ней два уравнения и два неизвестных aи b, а коэффициенты получаются суммированием х, у и т.д. Решать её можно разными способами. В данном случае использован сервис Excel Поиск решения для настройки линейной модели по данным X и Y, представленным в Таблице 3.1. Коэффициенты системы нормальных уравнений расположены в виде матрицы (верхние строки таблицы 3.2), неизвестные a и bзадаются произвольно и умножаются на коэффициенты (нижние строки). В окне Поиска решения задаются: Целевая ячейка – первая сумма, Значение равно 247 (Sy), Изменяя ячейки – aи b, Ограничения: вторая сумма равна 3901 (Sxy). Исходные данные X и Y приведены в Таблице 3.1. результаты расчёта в Таблице 3.2.

                           Таблица 3.1.                                                  Таблица 3.2.

     X Y
X²

XY

10 12
100

120

11 15
121

165

12 18
144

216

13 16
169

208

14 24
196

336

15 22
225

330

16 27
256

432

17 28
289

476

18 25
324

450

19 32
361

608

20 28
400

560

Суммы 165

247

2585

3901



11

165

247

165

2585

3901

a

b

-4,27

1,78

Суммы по строкам

-47,00

294,00

246,9999

-705,00

4606,00

3901



Теперь можно построить функцию регрессии Ŷ, сравнить её с Y и использовать для прогноза.

В принципе, МНК с Поиском решения можно использовать непосредственно. Для этого надо задать произвольные коэффициенты a и b, построить по ним функцию Ŷ = a + bX, вычислить остатки e = Y – Ŷи их квадраты, сумму e².

       В окне Поиска решения установить Целевая ячейка Se²минимум, Изменяя ячейки a и b, ограничений нет.

                                                                    Таблица 3.3.

X Y
Ŷ

Остатки e

e²

10 12
13,545

-1,545

2,388

11 15
15,327

-0,327

0,107

12 18
17,109

0,890

0,793

13 16
18,890

-2,890

8,357

14 24
20,672

3,327

11,070

15 22
22,454

-0,454

0,206

16 27
24,236

2,763

7,637

17 28
26,018

1,981

3,927

18 25
27,8

-2,8

7,840

19 32
29,581

2,418

5,847

20 28
31,363

-3,363

11,314

Суммы

1E-06

59,490

Дисперсии

40,872

34,923

5,949

R²

0,854

a

b

             F

52,833

-4,27

1,78

    Этот метод описан более подробно в разделе 4.4.

Дата добавления: 2018-05-12; просмотров: 284; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!

X	Y	(X-$Xcp)^2	(Y-$Ycp)^2	(X-$Xcp)(Y-$Ycp)*
10	12	25	109,2	52,2
11	15	16	55,5	29,8
12	18	9	19,8	13,3
13	16	4	41,6	12,9
14	24	1	2,38	-1,54
15	22	0	0,20	0
16	27	1	20,6	4,54
17	28	4	30,7	11,0
18	25	9	6,47	7,63
19	32	16	91,1	38,1
20	28	25	30,7	27,7
11	11
165	247	110	408,7	196
15	22,45
15	22,45			Ковариация
	Sum(X-$Xcp)^2 /(N-1)	11	40,8	19,6
	КОРЕНЬ	3,31	6,39
	СТАНДОТКЛОН	3,31	6,39	Корреляция
			Cov/Sx/Sy	0,924
			КОРРЕЛ()	0,924

X	Y	X²	XY
10	12	100	120
11	15	121	165
12	18	144	216
13	16	169	208
14	24	196	336
15	22	225	330
16	27	256	432
17	28	289	476
18	25	324	450
19	32	361	608
20	28	400	560

Суммы 165	247	2585	3901

11	165	247
165	2585	3901

a	b
-4,27	1,78
		Суммы по строкам
-47,00	294,00	246,9999
-705,00	4606,00	3901

X	Y	Ŷ	Остатки e	e²
10	12	13,545	-1,545	2,388
11	15	15,327	-0,327	0,107
12	18	17,109	0,890	0,793
13	16	18,890	-2,890	8,357
14	24	20,672	3,327	11,070
15	22	22,454	-0,454	0,206
16	27	24,236	2,763	7,637
17	28	26,018	1,981	3,927
18	25	27,8	-2,8	7,840
19	32	29,581	2,418	5,847
20	28	31,363	-3,363	11,314

		Суммы	1E-06	59,490

Дисперсии	40,872	34,923	5,949

R²	0,854		a	b
F	52,833		-4,27	1,78