Последовательность разработки математических моделей и решения задач.

2. Назначение эконометрических моделей. Принципы их спецификации.

3. Типы данных в эконометрике.

4. Виды экономико-математических моделей.

5. Построение концептуальной модели.

 

Основы математической статистики

 

    Предполагается, что приступая к изучению эконометрики студенты уже знают основы математической статистики. Практика показывает, что не знают. Это результат реформ образования. Поэтому необходимо вспомнить основные понятия теории вероятностей и математической статистики. Разделы 2.1 и частично 2.2 основаны на учебнике В.А.Бывшева [ 2 ] , так как содержат стандартные определения и формулы.

Случайная переменная.

Пусть q₁, q₂, …, q_n – набор n чисел, формирующих множество X = { q₁, q₂, …, q_n}. Величина х называется переменной, а множество Х – множеством её возможных значений, или областью изменения, если х  может принимать любые значения  q_i  из множества Х. Переменная величина, все возможные значения которой можно занумеровать, называется дискретной переменной. Если же возможные значения переменной х непрерывно заполняют собой некоторый интервал (a, b),  то есть X = (a, b),  то такая переменная величина называется непрерывной.

Переменная величина х с областью изменения Х называется случайной, если в результате некоторого опыта со случайными элементарными исходами она принимает значение из множества Х, которое заранее невозможно предсказать. Случайная величина может быть дискретной или непрерывной.

Теория вероятностей, математическая статистика и эконометрика базируются на предположении о существовании вероятности события

p:  x = q_i

 для дискретной случайной величины и

p:    xÎ( q_i , q_i +Dq )

для непрерывной, то есть существует вероятность того, что значение х попадёт в интервал  ( q_i , q_i +Dq ) .  Вероятность каждого элементарного исхода пропорциональна Dq .

Полной характеристикой случайной переменной х служит ее дифференциальный закон распределения. Так называется функция Р_х(q) скалярного аргумента q, определенная на всей числовой прямой, характеризующая объективную возможность появления в опыте значений q случайной переменной х. Если х – дискретная случайная переменная, то 

 

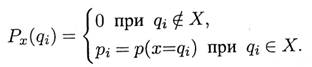
Следовательно, P_x(q_i) – это вероятность появления в опыте значения q_i  случайной переменной x. Функция P_x(q_i) имену­ется вероятностной функцией (или функцией частот, распределением частот)дискрет­ной случайной переменной x. Не­редко эту функцию задают таблицей, именуемой таблицей рас­пределения. Значения функции P_x(q_i)  неотрицательны и обладают следующим свойством:

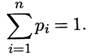
Дифференциальный закон распределения P_x(q) непрерывной случайной переменной х, если этот закон существует, имеет более сложный смысл:

 

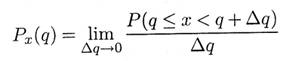
и называется плотностью вероятности. Как видите, это отношение вероятности попадания х в интервал Dq к величине этого интервала.Значения функции P_x(q) неотрицательны и обладают свойством

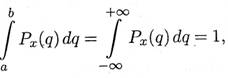
то есть какое-то значение переменная хпримет.

 

 

---

Дата добавления: 2018-05-12; просмотров: 183; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!