Логические и схемотехнические основы ЭВМ
Иерархическая структура функциональных модулей
При проектировании и построении ЭВМ и систем используют модульный принцип. Он состоит в том, что проектирование и построение схем и устройств в ЭВМ выполняют на основе некоторых наборов стандартных модулей (рис.2.1). Эти модули, как правило, выпускаются в промышленности серийно.
Рис.2.1.Иерархическая структура представления стандартных модулей в составе ЭВМ
Цифровой элемент (ЦЭ) – простейший функциональный модуль, который обеспечивает несложный алгоритм по обработке и хранению информации.
Функциональные узлы (ФУ)- функциональные модули, которые выполняют более сложные стандартные операции по обработке информации. Например, регистры, счетчики.
Функциональные устройства (ФУС) – функциональные модули, которые могут использоваться в качестве самостоятельных устройств.
2.2. Физические способы представления информации
Логические сигналы в электрических схемах представляются (кодируются) в виде различных значений токов и напряжений в различных точках схемы.
Рис. 2.2. Временные диаграммы представления логических сигналов
Используют два основных способа представления логической информации: в виде потенциальных сигналов и в виде импульсных сигналов (рис. 2.2).
На первой временной диаграмме представлено изображение потенциальных логических сигналов. Его характеристиками являются высокий и низкий потенциальные уровни, которым соответственно присвоены значения “1” и “0”.
|
|
|
На второй временной диаграмме представлено изображение логических сигналов в виде импульсов напряжения, при этом отсутствие импульса в данном временном такте означает “0”, а наличие импульса представляет “1”.
На третьей временной диаграмме представлено изображение логических сигналов в виде импульсов напряжения разной полярности, при этом отрицательный импульс в данном временном такте означает “0”, а положительный –“1”.
Общие сведения об алгебре логики
В схемотехнике возникают задачи анализа и синтеза логических схем. При этом используют специальный математический аппарат, который называется алгеброй логики (алгебра Буля) или исчислением высказываний. Высказывание - это любое утверждение, в отношении которого можно сказать истинно оно или ложно. В вычислительной технике принято принимать за “истину” –“1”, за “ложь –“0”. В основу булевой алгебры положены три логические операции: инверсия, конъюнкция, дизъюнкция. Правила выполнения логических операций задаются с помощью таблиц истинности. Условные графические обозначения (УГО) логических элементов определяются по ГОСТ 2742-82.
|
|
|
2.3.1. Основные логические операции
1) Инверсия (“НЕ”) F = Х
Таблица 2.1
| X | F |
| 0 | 1 |
| 1 | 0 |
В табл. 2.1 показана таблица истинности операции инверсия. На рис.2.1 – УГО логического элемента.
Рис. 2.3. Логический элемент- инвертор
2) Дизъюнкция (“ИЛИ”) F = X1 V X2 V ... V X n.
Таблица 2.2
| Х1 Таблица 2.2Х1 | Х2 | …… | Хn | F |
| 0 | 0 | 0… | 0 | 0 |
| 1 | 0 | 0… | 0 | 1 |
| 0 | 1 | 0… | 0 | 1 |
| 0 | 0 | 0… | 1 | 1 |
В табл. 2.2 показана таблица истинности операции “ИЛИ”, которая иногда называется “логическое сложение”. На рис.2.4 – УГО соответствующего логического элемента “ИЛИ”.
Рис.2.4. Логический элемент- дизъюнктор
3) Конъюнкция ( “И” ) F = X1 & X2 & X3 ...& Xn .
Рис.2.5. Логический элемент – конъюнктор
Таблица 2.3
| X1 | X2 | … | Xn | F |
| 0 | 0 | 0… | 0 | 0 |
| 1 | 0 | 0… | 0 | 0 |
| 1 | 1 | 0… | 0 | 0 |
| … | ||||
| 1 | 1 | 1… | 1 | 1 |
В табл. 2.3 показана таблица истинности операции “И”, которая иногда называется “логическое умножение”.
|
|
|
На рис.2.5 – УГО логического элемента “И”.
4) Штрих Шеффера
Таблица 2.4
| X1 | X2 | F |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
В табл. 2.4 представлена таблица истинности логической операции “штрих Шеффера”.
F = X1 & X2 = X1 │ X2 .
5) Стрелка Пирса
В табл. 2.5 представлена таблица истинности логической операции “стрелка Пирса”.
Таблица 2.5
| X1 | X2 | F |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
F = X1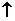 
X2 = X1VX2 .
Функционально-полный набор логических операций характеризуется тем, что на его основе можно записать любую логическую функцию алгебры логики. На основе логических элементов, реализующих этот набор операций, можно построить любую логическую схему. Например, возможны следующие функционально-полные наборы логических операций.
1) “НЕ”,” ИЛИ”, “И”;
2) “НЕ”, “ИЛИ”;
3) “НЕ”, “И”;
4) Штрих Шеффера (“И– НЕ”);
5) Стрелка Пирса (“ИЛИ – НЕ”).
Дата добавления: 2018-05-12; просмотров: 457; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!