Методы анализа и синтеза логических функций (логических схем)
Анализ и синтез логических схем выполняются в соответствии со следующими законами и соотношениями алгебры логики:
1) закон переместительный
X1V X2 = X2 V X1
X1 & X2 = X2 & X1 ;
Закон сочетательный
X1 V X2 V X3 = ( X1 V X2 ) V X3
X1 & X2 & X3 = X1 & ( X2 & X3 );
3) операция «склеивания»
(X1 & X2 ) V ( X1 & 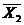 ) = X1 & ( X2 V
) = X1 & ( X2 V  ) = X1;
) = X1;


 4) правило де Моргана
4) правило де Моргана
X1 V X2 = X1& X2


 X1 & X2 = X1 V X2.
X1 & X2 = X1 V X2.
Логические функции и схемы задаются с помощью таблиц истинности. Синтез выполняется на основе законов алгебры логики. Рассмотрим методику синтеза логической функции на основе примера. Зададим логическую функцию в виде табл. 2.6. Запись логического выражения можно сделать в двух формах: дизъюнктивной и конъюнктивной.
Таблица 2.6
| X1 | X2 | X3 | F |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 |
ДСНФ – дизъюнктивная совершенная нормальная форма записи логической функции. Она состоит из дизъюнкции (логической суммы) конъюнкций (логических произведений), каждая из которых соответствует значению F=1 в очередной строке таблицы истинности. Если в состав каждой конъюнкции входят все входные переменные, то форма имеет совершенный характер. Если количество конъюнкций равно количеству единиц в выходном столбце таблицы истинности, то форма называется нормальной.
Запишем ДСНФ для предложенной таблицы истинности.
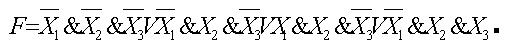
Выражение представляет собой конъюнкцию (логическое произведение) дизъюнкций, каждая из которых соответствует значению F= 1 в очередной строке заданной таблицы истинности.
Если в состав каждой дизъюнкции входят все входные переменные, то форма имеет совершенный характер.
Если количество дизъюнкций равно количеству нулей в выходном столбце таблицы истинности, то форма называется нормальной.
Запишем теперь КСНФ для предложенной таблицы истинности. 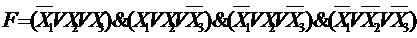 .
.
Это выражение записывается для строк, в которых F=0.
Оно может быть минимизировано на основе приведенных выше основных законов и соотношений алгебры логики.
Системы цифровых элементов
Система цифровых элементов – это совокупность логических, запоминающих и вспомогательных элементов, согласующихся между собой и имеющих единое конструктивное выполнение. Системы цифровых элементов (СЦЭ) классифицируются по двум признакам: типам связи между элементами в схеме и типам приборов, которые используются для реализации тех или иных функций в составе элементов. В зависимости от типов связей различают следующие системы цифровых элементов:
- потенциальные СЦЭ - отличаются тем, что при построении схемы разрешены только потенциальные 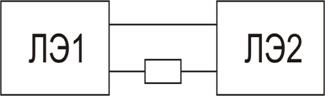 связи (рис.2.6)
связи (рис.2.6)
Рис.2.6. Типы связей между потенциальными ЛЭ
импульсные СЦЭ – при построении схем разрешены только импульсные связи (рис. 2.7);
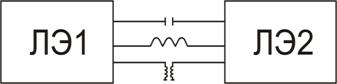
Рис. 2.7. Типы связей между импульсными ЛЭ
импульсно- потенциальные СЦЭ, в которых разрешены и импульсные и потенциальные связи между ЛЭ (рис.2.8).
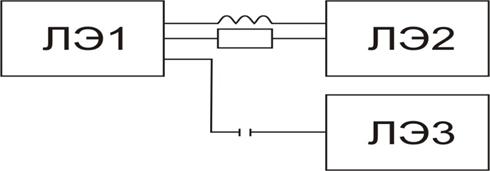
Рис. 2.8.Типы связей между импульсно- потенциальными ЛЭ
Согласование цифровых элементов означает использование одних и тех же источников питания и одинаковых уровней логических сигналов. Вспомогательными элементами являются различные типы усилителей, формирователей сигналов, схемы согласования и индикаторы. Эти схемы рассматриваются в курсе «Электроника».
В настоящее время применяются только потенциальные системы элементов. Потенциальные элементы обеспечивают более высокую надежность при передаче информации, а также являются предпочтительными при использовании интегральных технологий, так как в их схемах отсутствуют емкости и индуктивности.
Запоминающие элементы
В качестве запоминающих элементов (ЗУ) в составе логических схем используются, в основном, статические триггеры. Триггер имеет два устойчивых состояния “1” и “0”. Простейшим ЗУ является однотактный R–S- триггер или триггер с раздельным управлением
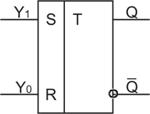
Рис.2.9. УГО R–S - триггера с раздельным управлением
 Q – прямой выход Q– инверсный выход
Q – прямой выход Q– инверсный выход
S (Set) – вход установки в “1”
R(Reset) – вход установки в “ 0 “.
Триггер находится в состоянии “1”, если на его прямом выходе будет потенциал, соответствующий значению “1”, на инверсном - “0” (рис.2.8). Существуют два типа R–S -триггеров: триггер с прямым управлением и инверсным управлением.
В работе триггера выделяются 3 режима:
1) режим хранения информации,
2) режим уcтановки в “0”,
3) режим установки в “1”.
R–S -триггер с прямым управлением строится на базе элементов “ИЛИ-НЕ” (рис. 2.10).
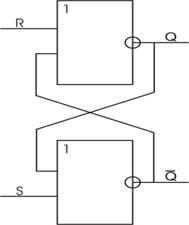
Рис. 2.10. Логическая схема R–S- триггера с прямым управлением
Таблица 2.7
| St | Rt | Qt+1 | Режимы |
| 0 | 0 | Qt = Q* | Хранения |
| 1 | 0 | 1 | Установка в “1” |
| 0 | 1 | 0 | Установка в “0” |
| 1 | 1 | ↑ | Запрещенный |
Состояния на входах триггера в момент времени t и состояния на прямом выходе триггера в момент (t+1) , т.е. после срабатывания триггера, и соответствующие режимы представлены в табл. 2.7, которая называется таблицей переходов. Как следует из этой таблицы, состояние триггера изменяется при поступлении на один из его входов сигнала “1”.
Триггер с инверсным управлением (R–S -триггер) построен на базе элементов “И-НЕ”. В табл. 2.8 представлена таблица переходов R-S- триггера с инверсным управлением, из которой следует, что изменение состояния триггера происходит при поступлении на один из его входов сигнала “0”.

Рис. 2.11. Логическая схема R–S - триггера с инверсным управлением
Таблица 2.8
| St | Rt | Qt+1 | Режимы |
| 0 | 0 | ↑ | Запрещенный |
| 1 | 0 | 0 | Установка в “0” |
| 0 | 1 | 1 | Установка в “1” |
| 1 | 1 | Qt | Хранения |
Дата добавления: 2018-05-12; просмотров: 682; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
