Условие, определяющее необходимость расчета здания на ветровую нагрузку

 

Согласно «Руководства по проектированию конструкций и технологии возведения монолитных бескаркасных зданий». ЦНИИЭП жилища М., С.М. 1982, расчет здания на действие ветровой нагрузки допускается не производить в том случае, если выполняется условие:

                             (6.1)

где f_cd – призменная прочность бетона, принимаемая с коэффициентом условий работы, равным 1;

B_i, h_i – ширина и толщина несущих стен здания, расположенных в плоскости действия ветровой нагрузки, м;

B_max – максимальная ширина несущей стены, М;

n – количество несущих стен в плоскости действия ветровой нагрузки;

K_i – коэффициент, учитывающий влияние проемов на жесткость несущих стен, определяемый по формуле

.                                              (6.2)

Значение «Р» для диафрагмы с одним проемом вычисляется по формуле

,                        (6.3)

где A₁; A₂; I₁; I₂ – площади и моменты инерции сечения простенков без учета примыкания полок;

  I – момент инерции системы без учета влияния проемов;

  H – полная высота здания;

  l – ширина проема в стене;

  I_n – момент инерции перемычки над проемом, определяемый при отсутствии трещин. В зданиях с монолитными перекрытиями I_n определяется с учетом плиты перекрытия. При этом ширина свесов плиты перекрытия, вводимая в расчет, принимается равной меньшей из величин: 1,5l и 12h^/_f, где h^/_f – толщина плиты перекрытия. При сборных плитах перекрытия их работа при определении I_n не учитывается. В последнем случае формула 6.3. принимает вид:

,                         (6.4)

где b₁ и b₂ – длина простенков, м;

  b – полная длина стены, м;

  h_n – высота перемычки, м.

Остальные значения принимаются по формуле (6.3). При наличии в стене нескольких рядов проемов значение «Р» вычисляется по формуле:

;

где P_i – коэффициент, вычисленный по формуле 6.3. для ряда проемов, как для стены с одним рядом проемов, в предположении, что перемычки над другими проемами на жесткость стены не влияют.

Величину суммарного изгибающего момента М в формуле (6.1), приходящегося на несущие стены здания от действия ветровой нагрузки, рекомендуется определять по формуле

                 (6.5)

где W_n – нормативное значение скоростного напора ветра в кПа (кг/м²);

  α₁, α₂, α₃ – коэффициенты, зависящие от высоты здания и типа местности, определяемые по таблице 6.6;

  B – ширина подветренного фасада здания, м.

Если на фасаде, параллельном направлению ветра, имаются лоджии, балконы с глухими ограждениями и т.п., значение В возрастает на величину ΔВ, определяемую по формуле

                                      (6.6)

где h_л, l_л – высота и длина одной лоджии (балкона и т.п.);

П_л – число лоджий на фасадах, параллельных действию ветра.

 

Таблица 6.6.

Коэффициент	Высота здания, м
	10	20	40	60	80	100
Тип местности А
α1	1	0,94	0,91	0,94	0,98	1,01
α2	1	1,19	1,55	1,81	2	2,18
α3	–	–	1,06	1,15	1,21	1,26
Тип местности Б
α1	0,65	0,59	0,56	0,58	0,61	0,67
α2	0,65	0,84	1,2	1,48	1,7	1,87
α3	–	–	1,11	1,24	1,32	1,39

 

Условие, определяющее общую устойчивость здания

Многоэтажное здание в целом работает в условиях продольно-поперечного изгиба. При большой массе и недостаточной жесткости вертикальных несущих конструкций здание может потерять общую устойчивость.

При этом возможны три частные формы потери устойчивости – две поступательные, сопровождающиеся изгибом коробки здания в направлении главных осей инерции, и третья – крутильная, сопровождающаяся закручиванием ее вокруг центра жесткости.

Каждой частной форме потери устойчивости соответствует свое частное значение критической массы здания (G_cr), т.е. такой его массы, при которой становится возможной потеря общей устойчивости, при действии общей нагрузки, отклоняющей здание от первоначального вертикального положения. Практикой проектирования и возведения многоэтажных зданий установлено, что для обеспечения необходимой устойчивости и жесткости здания требуется выполнение следующего условия:

                                           (6.7)

G_п – нормативная масса здания;

G_cr – критическая масса здания.

При изгибно-крутильной форме потери устойчивости критическая масса здания (G_cr) может быть найдена решением кубического уравнения:

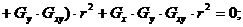                                                                    (6.8)

где G_x, G_y, G_xy – частные значения критической массы здания при поступательной форме потери устойчивости с изгибом относительно осей X и Y и при крутильной форме потери устойчивости;

и  расстояние от центра массы здания до центра жесткости по направлению осе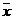й  и  (см. рис.6.4)

                                     (6.9)

Рисунок 6.4 – План здания (к определению координат центра жесткости и угла наклона главных осей по отношению к вспомогательным).

 

 главные суммарные моменты инерции стен жесткости относительно осей ;

А – сумма площадей горизонтальных сечений несущих стен здания.

Частные критические веса при поступательных формах потери устойчивости вычисляются по формуле Эйлера

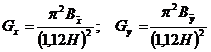,                           (6.10)

где H – высота здания, исчисляемая от поверхности земли;

 – суммарные жесткости несущих стен в направлении осей .

Критическая масса здания при крутильной форме потери устойчивости определяется по формуле:

,                                       (6.11)

где B_xy= 0,85E_b·I_w – крутильная жесткость здания;

E_b – модуль упругости бетона;

I_ω – полярный (крутильный) момент инерции несущих стен здания, определяемый по формуле:

,                   (6.12)

γ – характеристика плана здания, определяется по формуле:

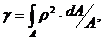                                   (6.13)

ρ – расстояние элементарной площадки плана dA от центра жесткости (рис. 6.4)

                           (6.14)

 

---

Дата добавления: 2018-04-15; просмотров: 518; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!