Покрытия с длинными цилиндрическими оболочками и призматическими складками
Длинная цилиндрическая оболочка под действием нагрузки от собственного веса и снега деформируется при определённых условиях подобно балке пролётом l1 c фигурным поперечным сечением высотой h1, включающим бортовые элементы (см. рис. 5.1), шириной, равной длине волны l2; в нижних частях поперечного сечения оболочки возникает растяжение, в верхней части – сжатие.
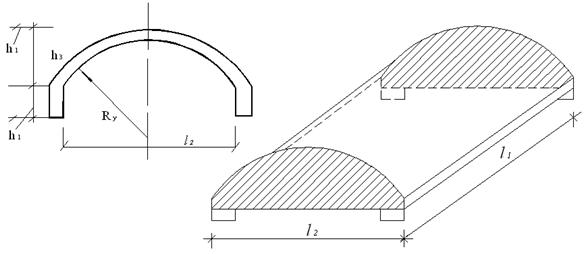
Рисунок 5.1
Бортовые элементы предназначены для повышения прочностных и жесткостных характеристик поперечного сечения покрытия. В них размещается основная растянутая арматура конструкции. Бортовые элементы укрепляют прямолинейные края цилиндрических оболочек, что необходимо при действии местных нагрузок. Форма и размеры бортовых элементов определяются конструктивным решением покрытия и его расчетом.
Монолитные оболочки делают гладкими. Сборные оболочки устраивают с продольными и поперечными ребрами для усиления сборных элементов на период изготовления, перевозки и монтажа.
В качестве диафрагм применяют сплошные балки, фермы, арки с затяжками (см. рис.5.2). Для обеспечения естественного освещения и аэрации помещений цилиндрические оболочки могут быть шедового типа или с проемами в вершине (см. рис. 5.3). Проемы окаймляют продольными ребрами; при большой длине их раскрепляют распорками.
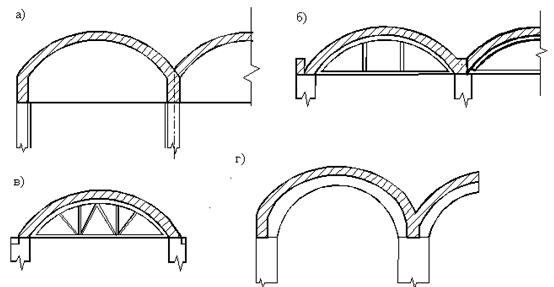
а) – сплошная балка; б) – арка с затяжкой; в) – ферма; г) – рама
Рисунок 5.2 – Типы диафрагм

|
|
|
а) – шедовая; б) – цилиндрическая.
1 – продольное ребро; 2 – стойка в плоскости остекления; 3 – распорка
Рисунок 5.3 – Оболочка со световыми проемами
При определенных условиях (покрытие в целом оперто по углам, нагрузка – равномерно распределенная, отношение размеров в плане 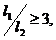 а для промежуточных волн
а для промежуточных волн  ) покрытия можно приближенно рассчитывать на прочность, жесткость и трещиностойкость как балки корытообразного профиля (см. рис.5.1). Расчет прочности производят по стадии разрушения при расчетных нагрузках; жесткость и трещиностойкость от действия нормативных нагрузок.
) покрытия можно приближенно рассчитывать на прочность, жесткость и трещиностойкость как балки корытообразного профиля (см. рис.5.1). Расчет прочности производят по стадии разрушения при расчетных нагрузках; жесткость и трещиностойкость от действия нормативных нагрузок.
Односторонняя равномерно распределенная снеговая нагрузка, не превышающая ¼ полной симметричной нагрузки, может быть заменена в расчете симметричной нагрузкой той же интенсивности. Легкую подвижную нагрузку от терьферов грузоподъемностью до 1т, подвешенных к бортовым элементам, при расчете можно рассматривать как симметричную, приложенную одновременно к обоим бортовым элементам.
В остальных случаях длинные оболочки рассчитывают как пространственно деформируемые системы.
Крайние полуволны многоволновых длинных оболочек с бортовыми элементами, не подкрепленными в пролете колоннами или стенами, приближенно можно рассчитывать в составе симметричной одноволновой оболочки, а промежуточные волны – так же, как одноволновые, но с учетом закрепления продольных краев от смещения в горизонтальном поперечном направлении (см. рис.5.4).
|
|
|
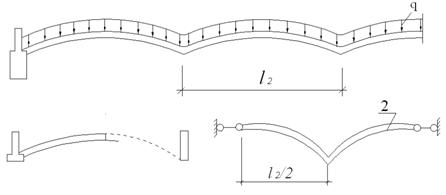
1) – крайняя полуволна; 2) – промежуточная волна
Рисунок 5.4 – Расчетные схемы многоволновой длинной оболочки
Для многопролетной оболочки, нагруженной равномерно распределенной нагрузкой (рис.5.5), достаточно рассчитать однопролетную шарнирно опертую оболочку пролетом l0, равным расстоянию от крайней диафрагмы до нулевой точки на эпюре моментов соответствующей многопролетной балки, а затем изменение вдоль оболочки внутренних сил и моментов, принять согласно изменению ординат в эпюре моментов указанной многопролетной балки с учетом изменения знака моментов под промежуточными опорами.

Рисунок 5.5 – Расчетная схема многопролетной оболочки
Далее рассмотрим приближенный расчет прочности длинной цилиндрической оболочки кругового симметричного профиля на действие вертикальной симметричной нагрузки на стадии предельного равновесия как железобетонной балки.

Рисунок 5.6 – К расчету длинной цилиндрической оболочки по предельным состояниям как железобетонной балки.
|
|
|
На рис.5.6 представлена схема расчетного напряженного состояния в поперечном сечении оболочки.
A3 – полка площадь сечения растянутой арматуры;
Q1 – половина центрального угла дуги оболочки;
Qc – половина центрального угла дуги сжатой зоны;
Q0 – расстояние от равнодействующей сил в растянутой арматуре до центра привязки круговой части сечения оболочки;
t – толщина цилиндрической части оболочки;
Ry – радиус цилиндрической части оболочки;
d1 – расстояние от равнодействующей сил в растянутой арматуре до верха бортового элемента.
Условие прочности при моментах внутренних сил, действующих в сечении оболочки относительно центра круговой части сечения.
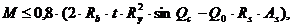 (5.1)
(5.1)
где M – момент внешних сил, вычисленный как в балке относительно той же точки;
0,8 – опытный коэффициент условия работы.
Положение границы сжатой зоны определяют из уравнения
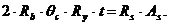 (5.2).
(5.2).
При проверке прочности из уравнения (5.2) определяют Qc и подставляют в уравнение (5.1). При подборе арматуры оба выражения объединяют в одно.
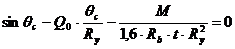 (5.3)
(5.3)
Это уравнение можно решить итераций, первоначально приняв 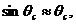 после чего из равенства (5.2) вычислить арматуры As.
после чего из равенства (5.2) вычислить арматуры As.
|
|
|
Касательные силы достигают наибольшего значения на диафрагмах; их вычисляют (приближенно) по формуле сопротивления материалов.
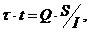 (5.4)
(5.4)
где Q – поперечная сила в опорном сечении оболочки, вычисленная как для балки;
τ – касательные напряжения в оболочке.
При детальном конструировании покрытий, определения их деформаций и перемещений, расчет на образование трещин в бетоне и их раскрытие необходимо выполнить расчет покрытий при промежуточных значениях нагрузок. Рассмотрим длинную цилиндрическую оболочку с параметрами a,b,Ry опертую по контуру на недеформируемые (в своей плоскости) контурные конструкции (рис.5.7).
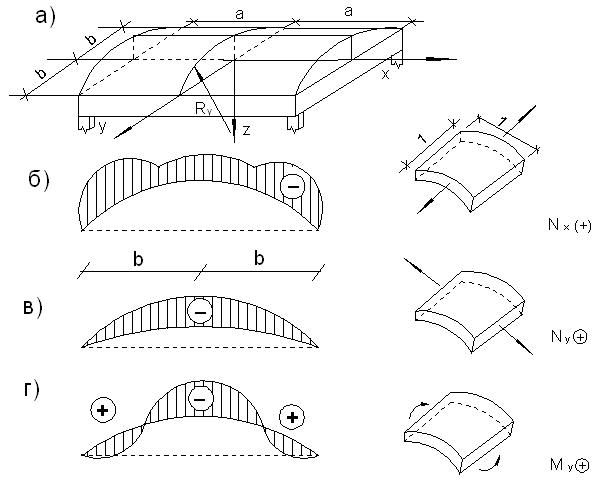
Рисунок 5.7 – Силы Nx и Ny и моменты My, действующие в длинной цилиндрической оболочке
Как выше отмечалось, внутренние силы в тонкостенной оболочке можно определить (с достаточной для практики точностью) по безмоментному состоянию конструкции. Для пологой цилиндрической оболочки в ее безмоментном состоянии нужно принять kx=0; ky=1/Ry; kx,y=0; D=0.
В этом случае уравнение равновесия на ось OZ нагрузки и внутренних сил, от нанесенных к элементу единичных размеров основания оболочки (5.5).
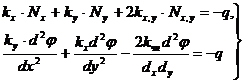 (5.5)
(5.5)
Существенно упрощается:
 (5.6)
(5.6)
Функция напряжений может быть взята в виде:

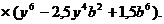 (5.7)
(5.7)
Эта функция отвечает граничным условиям задачи:
при x = ±а сила Nx= 0, при у = ±b сила Ny= 0.
Решение уравнения (5.7) при точках (0;0) и (0,5а; 0,5b) приводит к значениям постоянных параметров

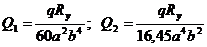
Сила в оболочке выражается зависимостями:
 (5.8)
(5.8)
Изгибающие моменты вдоль волны оболочки
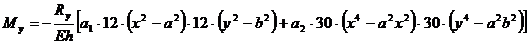 (5.9)
(5.9)
Двойным дифференцированием функции момента My по формуле (5.9) можно получить функцию прогибов оболочки.
Если задана цилиндрическая оболочка с недеформируемыми торцевыми диафрагмами и деформируемыми свободно висящими в пролете бортовыми элементами, при равномерно распределенной по поверхности нагрузке q (рис.5.8), то эту задачу можно решать в несколько этапов. На первом этапе полагают бортовые элементы недеформируемыми в пролете; при этом предположении можно использовать формулы (5.7) и (5.8).
Эпюра 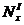 для сечения х=0 показана на рис.(5.8, а). Значение ординат сил
для сечения х=0 показана на рис.(5.8, а). Значение ординат сил 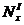 и
и 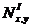 в отдельных точках составляют:
в отдельных точках составляют:

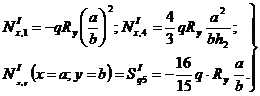
 (5.10)
(5.10)
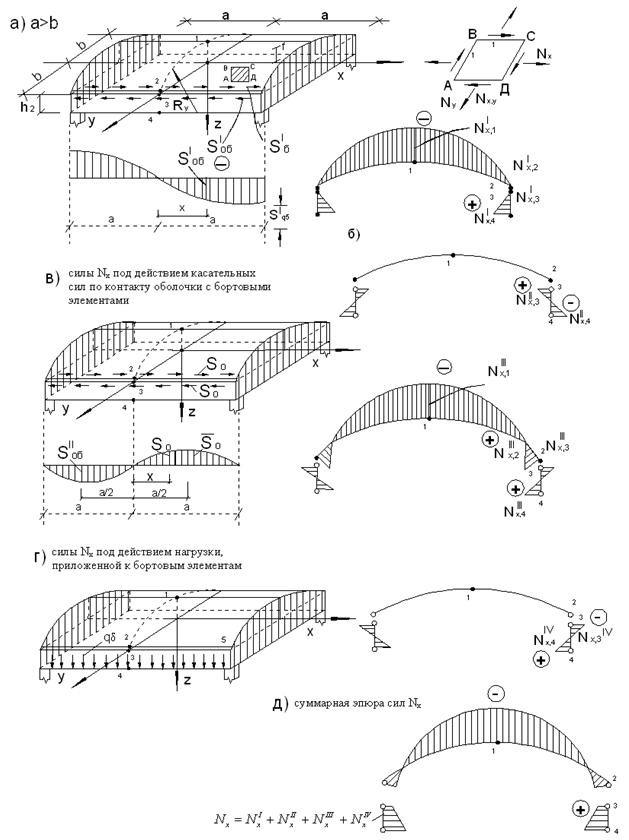
Рис.5.8 – К расчету длинной цилиндрической оболочки как пространственной системы
а) – оболочка на деформируемом контуре под действием нагрузки q;
б) – силы Nх при отделении бортовых элементов от оболочки.
На втором этапе отделяют оболочку от бортовых элементов (состояние II). При этом напряженное состояние в оболочке не изменится. В бортовых элементах под действием касательных усилий 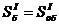 , развивающихся по линии контакта с оболочкой, возникнут новые продольные силы. Они на уровне верха и низа бортовых элементов составляют (рис. 5.8, б):
, развивающихся по линии контакта с оболочкой, возникнут новые продольные силы. Они на уровне верха и низа бортовых элементов составляют (рис. 5.8, б):
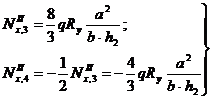 (5.11)
(5.11)
Действительный уровень нулевых значений Nx не совпадает с верхней гранью бортовых элементов; вследствие этого образуются дополнительные касательные силы S0 между оболочкой и бортовыми элементами.
Рассматривая их как загружение (состояние III), принимают функцию напряжений в виде:
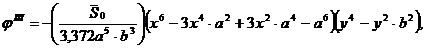 (5.12)
(5.12)
где 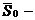 фиксированное значение при x = 0,5a (рис.5.8, в)
фиксированное значение при x = 0,5a (рис.5.8, в)
Выражения для определения внутренних сил:
 (5.13)
(5.13)
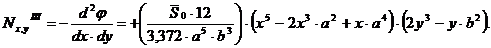 (5.14)
(5.14)
Эпюры NxIII для сечения х = 0 приведены на рис. (5.8, в); значение ординат в отдельных точках:
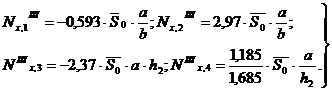 (5.15)
(5.15)
Кроме того, необходимо учесть нагрузку, приложенную непосредственно к бортовым элементам, в качестве их собственных все qδ (состояние IV, рис. 5.8, г).
Значение усилий по граням бортового элемента
 (5.16)
(5.16)
На линиях контакта оболочки с бортовыми элементами суммарные продольные деформации должны быть одинаковыми: (при одинаковых модулях упругости и суммарные продольные напряжения должны быть одинаковыми).
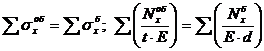 (5.17)
(5.17)
где t – толщина оболочки;
d – толщина бортового элемента.
С использованием приводимых выше напряжений равенство напряжений принимает вид
 . (5.18)
. (5.18)
Из этого уравнения находят значение 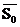 , после чего суммируют решения по всем четырем состояниям (рис.5.8, д). Данное решение позволяет вычислить также силы
, после чего суммируют решения по всем четырем состояниям (рис.5.8, д). Данное решение позволяет вычислить также силы 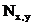 в любом месте покрытия.
в любом месте покрытия.
Моменты вдоль волны М, вычисляют способом, изложенным выше (см. рис. 5.7).
Около диафрагм возникают местные моменты Mx.
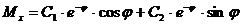 , (5.19)
, (5.19)
где С1 и С2 – постоянные интегрирования;
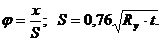
При шарнирном соединении оболочки с диафрагмой (в сборных конструкциях).
 , (5.20)
, (5.20)
Наибольший изгибающий момент (рис. 5.8, а).
 . (5.21)
. (5.21)
Он действует на расстоянии от диафрагмы
 (5.22)
(5.22)
Дата добавления: 2018-04-15; просмотров: 1600; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
