Сцепление арматуры с легкими бетонами
Под сцеплением понимают сопротивление забетонированного арматурного стержня выдерживанию или продавливанию. Как и в тяжелом бетоне, силы сцепления зависят от ряда физических и механических факторов:
1) склеивание арматуры с бетоном благодаря клеящей способности цементного камня;
2) силы трения, возникающие в результате обжатия арматуры в процессе усадки бетона;
3) силы механического зацепления из-за неровностей арматуры или наличия выступов.
На значение напряжений сцепления τg влияют состояние поверхности арматуры (шероховатость, периодический профиль), прочность бетона, степень уплотнения бетона в контактной зоне, сопротивления зерен заполнителя деформациям под сосредоточенными нагрузками в местах контакта с ребрами стержней периодического профиля. В силу последнего сцепления легких бетонов может быть ниже, чем тяжелых.
Прочность сцепления стержней периодического профиля с легким бетоном определяют по формуле:
(1.22)
В приопорных частях балок, плит и других аналогичных конструкций на напряжения сцепления оказывает влияние опорное поперечное давление q (рис. 1.5), которое по прочности для существующих типовых конструкций не превышает 0,3Rm (Rm – средняя кубиковая прочность бетона).
Поперечное давление вызывает появление радиальных напряжений (нормальных) σττ по поверхности контакта арматурного стержня с бетоном. Среднее напряжение сцепления τg.q возникающее вследствие поперечного обжатия стержня:
|
|
|
, (1.23)
k – коэффициент трения стержня по бетону (для гладких стержней k=0,3; для стержней периодического профиля k= 0,5);
γg – коэффициент условий работы, зависящий от прочности бетона и класса арматуры и колеблющийся в пределах от 0,8…0,92, в среднем его принимают равным 0,9.
Рисунок 1.5 – Опорный участок элемента и распределение радиальных напряжений вокруг арматурного стержня.
Влияние армирования на усадку и ползучесть
Усадка и ползучесть армированных легких бетонов изучены мало.
В армированном элементе свободные усадка и ползучесть сдерживаются арматурой, которая играет роль внутренней связи, т.к. ее модуль упругости выше модуля упругости бетона. Вследствие этого деформации усадки и ползучести армированного бетона ниже, чем неармированного, причем, чем выше коэффициент армирования μ, тем больше его влияние.
Под влиянием разности деформаций свободной усадки бетонного элемента εsl и стесненной усадки армированного элемента εsl,s (рис. 1.6)
εвt= εsl – εsl,s. (1.24)
|
|
|
Возникают средние растягивающие напряжения в бетоне.
Рисунок 1.6 – Деформации усадки образцов:
а) – бетонного; б) – железобетонного
(1.25)
Наибольшие значения этих напряжений находятся в зоне контакта с арматурой. Деформации εsl,s являются для арматуры упругими, и в ней возникают сжимающие напряжения.
(1.26)
Теоретически влияние армирования на процессе усадки получим, использовав условие внутреннего равновесия, в любой момент времени t.
(1.27)
и условие совместности деформаций
(1.28)
где σвt(t) – растягивающие напряжения в бетоне к моменту времени t;
σs(t) – сжимающие напряжения в арматуре к моменту времени t;
Ав – площадь поперечного сечения бетона ( 
);
εsl(t) – деформации свободной усадки бетона к моменту времени t;
εsl,s(t) – деформации сжатия в арматуре к моменту времени t;
εвt(t) – деформации растяжения в бетоне к моменту времени t;
Учитывая, что из (1.27) σвt(t)= μσs(t) и
εвt(t)= 
(1.29)
после интегрирования и решения уравнения (1.29), получаем выражение для определения деформаций усадки армированного бетона 
|
|
|
(1.30)
где 
; 
Н(t,τ) – резольвента ядра.
; (1.31)
С(t) – удельная деформация ползучести бетона. Для приближенного описания изменения С(t,τ) можно использовать эмпирическую формулу, полученную на основе статистической обработке результатов опытов с керамзитобетоном
С(t,τ) 
,
где 
;
ξ1, ξ3, ξ4 – коэффициенты, учитывающие соответственно возраст бетона к моменту нагружения, приведенный размер поперечного сечения и относительную влажность среды (принимают по нормам);
k= 13,5·10-6 м3/кг;
В – расход воды, кг/м3,
Rm – кубиковая прочность бетона.
Формула (4.30) даст хорошую сходимость с опытными данными, но она сложна для практического пользования. Поэтому при расчетах применяют эмпирические зависимости, основанные на экспериментальных данных. Так для керамзитобетона используют формулу:
, (1.32)
где εsl(100) – свободная усадка бетона к моменту наблюдений (100 суток) вычисляется по формуле (1.20). Для других бетонов используют зависимость
(1.33)
При выводе формулы для ползучести армированного легкого бетона при осевом сжатии используется уравнение равновесия и совместности деформации арматуры и бетона:
|
|
|
(1.34)
(1.35)
где εs(t) и εв(t,τ) – деформации арматуры и бетона к моменту времени t при загружении элемента в возрасте τ;
N(t) – осевая сжимающая сила во времени t.
Деформации бетона εв(t,τ) запишем в виде
, (1.36)
где 
– функция влияния.
Учитывая, что из (1.34) 
и условие (1.35), после некоторых преобразований получим интегральное уравнение Вольтера второго рода
, (1.37)
где 
.
Так как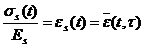 
, где 
полная относительная деформация армированного элемента, а деформация ползучести элемента 
, то после решения (1.37) получим
, (1.38)
где 
.
Для частного случая, когда N(t)=N=const, Eв(t)=Eв=const, выражения для f2(t) и f3(t) принимают вид
; 
. (1.39)
Для приближенного определения деформаций армированного бетона можно использовать зависимость
, (1.40)
где С(t,τ) вычисляют по формуле (1.32).
Теплофизические свойства
Теплофизические свойства легких бетонов оценивают физическими (средняя плотность, пористость, воздухопроницаемость, звукоизолирующая способность), влажностными (влажность, паропроницаемость, сорбционная влажность, водопоглащение), и теплотехническими (теплопроводность, температуропроводность, теплоемкость, теплоусвоение) характеристиками.
Средняя плотность легких бетонов является важнейшей характеристикой, от которой зависят многие другие. В СниП 2.04.01-84 установлены марки по плотности: Д800, Д900…Д2200. В ГОСТ 25820-83 марки бетона по плотности обозначены буквами «Пл» (например Пл1400). Марка по средней плотности означает массу 1м3 легкого бетона в сухом состоянии.
Пористость 
ρm – средняя плотность; ρ – истинная плотность ρ определяют делением массы бетона на объем без учета пор. Пористость легких бетонов колеблется от 25…80% (для тяжелого бетона 10…20).
Влажность зависит от технологических факторов и температуры – влажностных условий хранения и эксплуатации легких бетонов. Первоначальное содержание влаги в бетонах со средней плотностью > 1400 кг/м3 составляет 10…20%. Максимальная влажность бетона в различных видах конструкций устанавливается соответствующими нормами.
На водопоглащение бетона в первую очередь влияет открытая межзерновая пористость, вид заполнителя, вяжущего, структура бетона. С увеличением плотности водопоглащение уменьшается.
Коэффициент теплопроводности имеет решающее значение при определении толщины ограждающих конструкций. Зависит от структуры бетона, средней плотности, зернового состава заполнителей, влажности бетона и других факторов. Значение коэффициента теплопроводности приведены в СниП 11-3-79* «Строительная теплотехника». Так, для шлакопемзобетона, шунгизитобетона и керамзитобетона с ρм=1400кг/м3 коэффициенты теплопроводности λ, в сухом состоянии соответственно равны 0,35;0,49 и 0,47 Вт/(м·Со).
Дата добавления: 2018-04-15; просмотров: 587; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!