Соединение резисторов (сопротивлений)
Резисторы в электрических цепях могут быть включены последовательно, параллельно или смешано.
При последовательном включении все резисторы соединены один за другим без разветвлений (рисунок 2.4, а), и при подключении к источнику питания по ним протекает ток одной и той же величины.
Общее, или эквивалентное, сопротивление такой цепи равно сумме сопротивлений этих резисторов:
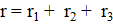
Напряжения (падения напряжения) на отдельных участках цепи:
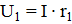

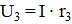
Общее напряжение всей цепи равно сумме падений напряжения на отдельных участках:

Ток неразветвленной цепи:

Последовательное включение резисторов (добавочных сопротивлений) используется на практике для понижения напряжения (пусковые и регулировочные реостаты), а также для расширения пределов измерения измерительных приборов (вольтметров).
При параллельном соединении все резисторы подключены к двум точкам (узлам) цепи на одно и то же напряжение (рисунок 2.4, б).

Рисунок 2.4 - Соединение резисторов: а) - последовательное; б) - параллельное; в) - смешанное
Общее сопротивление резисторов такой цепи можно найти из выражения:

В частном случае, когда параллельно включены три резистора, эквивалентное сопротивление:

При параллельном включении n одинаковых резисторов общее сопротивление уменьшается в n раз:

где r1- сопротивление одного резистора, Ом.
Заменяя величины сопротивлений проводимостями, получим:
|
|
|

Следовательно, общая проводимость цепи при параллельном соединении резисторов равна сумме проводимостей параллельных ветвей.

Рисунок 2.5 - Электрическая цепь: а) - с узловыми точками; б) - замкнутого контура
Напряжение цепи:

Ток в неразветвленной цепи определяется по формуле:
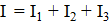
Выключение одного или нескольких резисторов из цепи не отражается на работе оставшихся. Поэтому осветительные лампы, электродвигатели и другие приемники электрической энергии преимущественно включают параллельно.
При смешанном соединении резисторы включают в цепь последовательно и параллельно (рисунок 2.4, в). В этом случае расчет электрической цепи приводится к расчету параллельных и последовательных соединений, а сама цепь - к эквивалентной последовательной.
Для расчета сложных разветвленных электрических цепей применяют законы Кирхгофа, которые устанавливают соотношения между токами и напряжениями в сети.
Первый закон. Сумма токов, притекающих к точке разветвления (узлу) цепи, равна сумме токов, вытекающих из этого узла, или алгебраическая сумма токов в узловой точке электрической цепи равна нулю. Например, в узле А (рисунок 2.5, а).
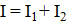

Притекающие к узлу токи принято считать положительными, а вытекающие из узла - отрицательными.
|
|
|
Второй закон. Алгебраическая сумма ЭДС (источников тока), действующих в любом замкнутом контуре, равна алгебраической сумме падений напряжения в ветвях этого контура:
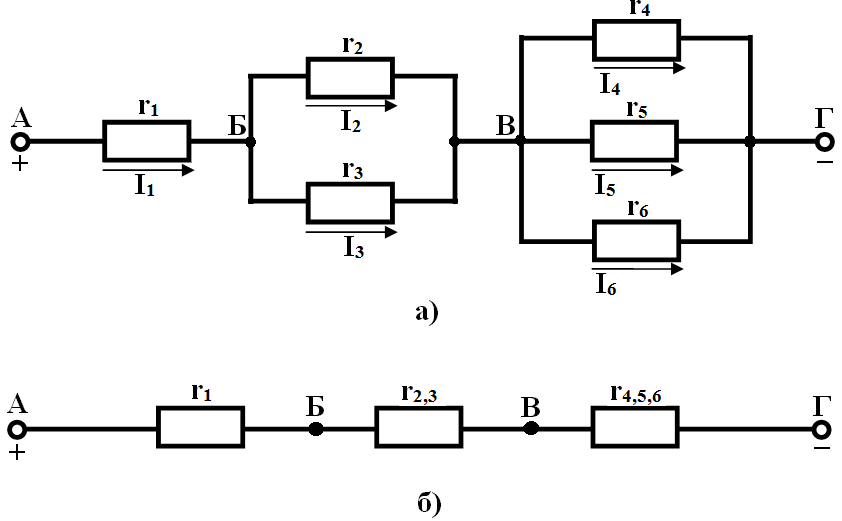
Рисунок 2.6 - Электрическая цепь со смешанным соединением резисторов


При составлении уравнений выбирают направление обхода контура и произвольно задаются направлениями токов.
Например, в замкнутом электрическом контуре (рисунок 2.5, б) действуют три ЭДС: E1, E2, E3. Две из них, E1 и E3, действуют согласно, в одном направлении, а третья E2 - навстречу. Направление тока в контуре принимается произвольно.
Если направление обхода контура, показанное внутри стрелкой, совпадает с направлением ЭДС и тока, то эти ЭДС и токи считаются положительными, если же не совпадает, то они записываются с отрицательными знаками, т. е.:

Если в результате решения уравнений получается отрицательная величина тока, значит, ток в контуре протекает в обратном направлении.
Пример.Определить напряжения и токи на участках цепи (рисунок 2.6, а), если r1 = 1,6 Ом; r2 = 36 Ом; r3 = 24 Ом; r4 = 40 Ом; r5=10 Ом; r6 = 8 Ом; напряжение на выводах цепи U = 60 В.
Решение.Эквивалентные сопротивления (рисунок 2.5, б):
|
|
|

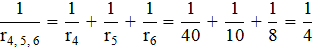
Откуда:

Эквивалентное сопротивление всей цепи:

Ток в неразветвленной части цепи:


Рисунок 2.7 -Схема питания электроприемников
Напряжения на участках:


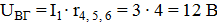
Токи в ветвях:



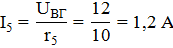
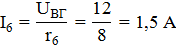
Пример.К групповому распределительному щитку (рисунок 2.7) присоединены три параллельные группы электроприемников, имеющие сопротивления r1 = 22 Ом; r2 = 10 Ом; r3 = 100 Ом. Ток в первой группе I1 = 10 А. Определить ток в магистральном проводе, а также напряжение на главном распределительном щите, расположенном от группового щитка на расстоянии 100 м, если магистраль выполнена двумя медными проводами сечением 10 мм2.
Решение. Ток во второй группе:

Ток в третьей группе:

Ток в магистральном проводе:
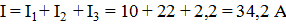
Эквивалентное сопротивление электроприемников:


Напряжение на групповом распределительном щитке:

Потеря напряжения в магистрали:

Напряжение на главном распределительном щите:

Пример. Определить ток в цепи (рисунок 2.4, б) и падение напряжения на резисторах, если E1 = 100 В, Е2 = 75 В, E3 = 50 В, r01 = О,1 Ом; r02 = 0,3 Ом; r03 = 0,1 Ом; r1 = 5 Ом; r2 = 2 Ом.
Решение. Результирующая ЭДС:

Общее сопротивление:

Ток в цепи:

Падение напряжения в источниках ЭДС:


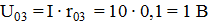
Падение напряжения на резисторах
|
|
|


Проверка:
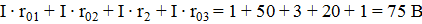
что равно результирующей ЭДС цепи.
Дата добавления: 2018-04-15; просмотров: 1519; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
