Исходные данные для логического вывода
| Лингвистическая переменная | Альтернатива | ||||
| u1 | u2 | u3 | u4 | u5 | |
| ОБРАЗОВАНИЕ | Среднее | Высшее | Не (Среднее или Высшее) | Среднее | Высшее |
| ОПЫТ | Приемлемый | Большой | Большой | Приемлемый Ç Большой | Большой |
| УМЕНИЕ РАБОТАТЬ C ПО | Есть | Нет | Есть | Нет | Нет |
| ЮРИДИЧЕСКАЯ ГРАМОТНОСТЬ | Нет | Нет Ç Есть | Есть | Есть | Есть |
На рис. 4.5 показан результат вывода с использованием правила d1 для альтернативы u1.
На рис. 4.6 и 4.7 показаны экранные формы интеллектуальной программной системы нечеткого логического вывода, используемые для ввода исходной информации.
В табл. 4.7. приведены результирующие лингвистические оценки альтернатив, полученные методом нечеткого вывода, и соответствующие им значения мер сходства.
Таблица 4.7
Результаты работы системы нечеткого вывода
| Лингвистическая оценка
| Альтернатива
| ||||
| u1 | u2 | u3 | u4 | u5 | |
| СПЕЦИАЛИСТ (Неудовлетворяющий) | 0,08 | 0,0 | 0,30 | 0,21 | 0,10 |
| СПЕЦИАЛИСТ (Удовлетворяющий) | 0,85 | 0,95 | 0,32 | 0,69 | 0,97 |
| КАНДИДАТ (Хороший) | 0,81 | 0,0 | 0,30 | 0,0 | 0,0 |
| КАНДИДАТ (Очень хороший) | 0,0 | 0,74 | 0,28 | 0,57 | 0,91 |
| КАНДИДАТ (Безупречный) | 0,0 | 0,0 | 0,22 | 0,0 | 0,0 |
Полученные результаты позволяют увидеть, что кандидаты u1, u2, u4, u5 являются удовлетворяющими специалистами (мера сходства больше 0,5), а кандидат u3 почти с одинаковым значением меры сходства принадлежит ко всем возможным категориям. При этом значения меры сходства находятся в интервале (0,22 - 0,32), что свидетельствует о весьма слабом сходстве с соответствующими понятиями. Такие результаты скорее следует интерпретировать как неспособность данного объекта вписаться в рамки имеющихся градаций при сформулированном наборе правил, чем как свойство быть похожим на все категории одновременно. Альтернатива u1 хорошо согласуется с понятием хорошего кандидата, а u2 и u5 — с понятием очень хорошего кандидата. Альтернатива u4 также претендует на роль очень хорошего кандидата, однако сходство с соответствующим нечетким прототипом имеет весьма невысокое.
|
|
|
Выбор фирмой стратегии расширения доли рынка методом аддитивной свертки
Рассмотрим пример применения метода аддитивной свертки для решения задачи по выбору некоторой фирмой, производящей бытовую технику, стратегии расширения своей доли на рынке.
Первоначально определяются альтернативы — возможные стратегии поведения фирмы.
Стратегия а1 — снижение цены. Это возможно в том случае, когда фирма имеет некоторое преимущество перед конкурентами или может обеспечить снижение себестоимости продукции. Однако реализация этой стратегии может привести к ценовой конкуренции, что само по себе достаточно опасно,
|
|
|
Стратегия а2 — модификация существующего продукта. Она потребует дополнительных расходов на переналадку производства, но при этом обеспечит некоторое повышение качества продукции. Реализация такой стратегии может привлечь новых покупателей, способствуя новому перераспределению долей рынка между фирмами. Конкуренция в данном случае не является ценовой и столь сильной.
Стратегия а3 — разработка нового продукта. Эта стратегия потребует дополнительных и значительных расходов, но позволит в случае успеха опередить конкурентов в технологическом развитии и некоторое время быть монополистом на рынке.
Стратегия а4 — поиск новых рынков сбыта. В этом случае фирма за счет поиска новых рынков и вхождения на них может увеличить объем продаж, но это не повлечет за собой перераспределение старого рынка. При такой стратегии также достаточно велика вероятность возникновения сильной конкурентной борьбы и возрастания расходов на маркетинговые исследования и новые производственные мощности.
|
|
|
Для оценки альтернатив определим следующие критерии:
c1 — затраты на расширение производства; c2 — время реализации проекта; c3 — затраты на маркетинговые исследования; с4 — управленческие расходы; с5 — риск от потерь; c6 — срок окупаемости; c7 — качество продукции; c8 — цена продукции.
Для оценки относительной важности критериев используется лингвистическая переменная W = {ПРАКТИЧЕСКИ НЕВАЖНЫЙ; НЕ ОЧЕНЬ ВАЖНЫЙ; ДОВОЛЬНО ВАЖНЫЙ; ВАЖНЫЙ; ОЧЕНЬ ВАЖНЫЙ}. Значения термов множества заданы нечеткими числами, которые имеют треугольный вид функций принадлежности (рис. 4.8).
Критерии получили следующие лингвистические оценки относительной важности a = { 
= ВАЖНЫЙ; 
= ДОВОЛЬНО ВАЖНЫЙ;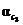 
= НЕ ОЧЕНЬ ВАЖНЫЙ; 
= ВАЖНЫЙ; 
= НЕ ОЧЕНЬ ВАЖНЫЙ; 
= ДОВОЛЬНО ВАЖНЫЙ; 
= ВАЖНЫЙ; 
= НЕ ОЧЕНЬ ВАЖНЫЙ}.
Оценка альтернатив по критериям производится с использованием лингвистической переменной S == "УДОВЛЕТВОРИТЕЛЬНОСТЬ" = {КРАЙНЕ НИЗКАЯ; НИЗКАЯ; СРЕДНЯЯ; ВЫСОКАЯ; ОЧЕНЬ ВЫСОКАЯ}. Функции принадлежности термов имеют следующий вид:
КРАЙНЕ НИЗКАЯ = {1,0/0,0; 0,0/0,0};
НИЗКАЯ = {0,0/0,0; 1,0/0,2; 0,0/0,4};
СРЕДНЯЯ = {0,0/0,3; 1,0/0,5; 0,0/0,7};
ВЫСОКАЯ = {0,0/0,6; 1,0/0,8; 0,0/1,0};
|
|
|
ОЧЕНЬ ВЫСОКАЯ = {0,0/0,8; 1,0/1,0};
В табл. 4.8 сведены оценки рассматриваемых альтернатив.
Таблица 4.8
Дата добавления: 2018-04-15; просмотров: 331; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!