Многокритериальный выбор альтернатив на основе аддитивной свертки
В рассматриваемом методе [3] экспертные предпочтения представлены с помощью нечетких чисел, имеющих функции принадлежности треугольного вида (рис.4.2).

Пусть имеется множество альтернатив А = {а1, а2, ..., am} и множество критериев С = {с1, с2, ..., сn}, при этом оценка j-й альтернативы по i-му критерию представлена нечетким числом Rij, a относительная важность i-го критерия задается коэффициентом a i = 1,2 ...,п. Если коэффициенты а, нормированы, то взвешенная оценка j-й альтернативы вычисляется по формуле

Если функции принадлежности mRij(rij) и mai(ai) имеют треугольный вид, то для них, как и для нечеткого числа X, вершина X*, а также левая Х¢ и правая X" границы определяются следующими соотношениями:

Взвешенная оценка j-й альтернативы Rj является результатом линейной комбинации нечетких чисел и также будет иметь функцию принадлежности треугольного вида. Вершину и границы нечеткого числа Z == Х ´ Y, полученного в результате операций сложения или умножения (символ ´ обозначает обобщенную операцию), можно вычислить следующим образом:
Z'=X¢ ´ Y¢;Z¢¢ =X¢¢ ´ Y¢¢;Z*=X* ´ У.
Ранжирование альтернатив с использованием полученных взвешенных оценок возможно на основе их нечеткой композиции:

Здесь mJ(j) — нечеткое множество альтернатив, соответствующих понятию "лучшая альтернатива". Лучшей считается альтернатива, имеющая наибольшее значение mJ(j).
Приоритет каждой альтернативы вычисляется путем выбора минимума среди точек пересечения правой границы соответствующего ей нечеткого числа Rj с границами нечетких чисел, представляющих взвешенные оценки альтернатив, расположенных правее на числовой оси (удовлетворяющих условию rk > rj.). При этом предполагается, что правая граница области определения нечетких чисел соответствует самым предпочтительным оценкам, а левая — наихудшим.
Ранжирование альтернатив на множестве лингвистических векторных оценок
Задано множество альтернатив A == {а1, а2, ..., аm} и множество соответствующих исходов S = [s1, s2, ..., sm,}. Каждый исход sj характеризуется альтернативой аi и вектором лингвистических оценок на множестве критериев К = [К1, К2, .... Кn}. Множество лингвистических векторных оценок исходов К = {K(s1), K(s2), ..., K(sm)} можно упорядочить, введя функцию принадлежности нечеткого отношения порядка m ³: К ´ К ® [0,1]. Для i-го критерия обозначим mi ³ (Ki(sj), Ki(sk)) через mi³ (sj , sk) Значение этой функции можно вычислить по фоомуле

Степень истинности m < (sj, sk) нечеткого высказывания sj < sk можно определить как вероятность того, что точное значение sj будет меньше точного значения sk. Предполагая, что исходы являются независимыми случайными величинами, отношение m < (sj, sk) можно представить в виде:
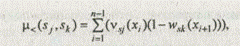
где vs(x) — вероятность того, что в качестве точного значения нечеткого числа s используется величина х;
ws(x) — вероятность того, что в качестве точного значения s используется величина у < х:

Векторные оценки могут быть упорядочены на основе функции принадлежности

где х — обозначает символ обобщенной операции.
Так как между множеством альтернатив и исходив существует взаимно однозначное соответствие, функцию принадлежности нечеткого отношения предпочтения на множестве альтернатив можно представить в виде:

Решение задачи с использованием данного метода включает следующие основные шаги:
• вычисление функций принадлежности m< с использованием соотношений (4.2);
• построение нечеткого отношения порядка m³;
• минимизация отношения m³;
• определение отношений предпочтения на множестве альтернатив и выявление лучшей альтернативы. Для этого вычисляется отношение предпочтения между альтернативой aj и всеми остальными альтернативами, функция принадлежности которого имеет вид:
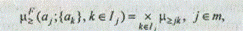
где Ij — множество индексов альтернатив, с которыми может сравниваться j-я альтернатива.
Решение задачи ранжирования можно описать соотношениями:
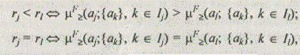
где rj — ранг альтернативы.
Наиболее предпочтительная альтернатива имеет самый низкий ранг.
Дата добавления: 2018-04-15; просмотров: 472; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
