Многокритериальный выбор альтернатив на основе пересечения нечетких множеств
Элементы теории нечетких множеств успешно применяются для . принятия решений. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. Последние можно определить как отношения предпочтительности между объектами. Рассмотрим одну из математических постановок задач принятия решений на основе теории нечетких множеств.
В данном случае критерии определяют некоторые понятия, а оценки альтернатив представляют собой степени соответствия этим понятиям. Пусть имеется множество альтернатив А = {а1, а2, ..., аm,} и множество критериев С= {С1, С2, ..., Сn}, при этом оценки альтернатив по каждому i-му критерию представлены нечеткими множествами:
Сi= {mCi (a1)/ mCi, (a2)/a2, …, mCi (am)/am}
Правило выбора лучшей альтернативы можно представить как пересечение нечетких множеств, соответствующих критериям:
D = С1 Ç C2 Ç ... Ç Сn.
Операция пересечения нечетких множеств может быть реализована разными способами. Иногда пересечение выполняется как умножение, но обычно этой операции соответствует взятие минимума:
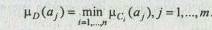
Лучшей считается альтернатива a*, имеющая наибольшее значение функции принадлежности
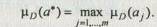
|
|
|
Если критерии Сi имеют различную важность, то их вклад в общее решение можно представить как взвешенное пересечение:
D=C1a1 Ç C2a2Ç ...Ç nan,
где аi - весовые коэффициенты соответствующих критериев, которые должны удовлетворять следующим условиям:
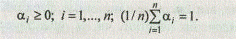
Коэффициенты относительной важности можно определить, используя процедуру попарного сравнения критериев.
Многокритериальный выбор альтернатив на основе нечеткого отношения предпочтения
Рассмотрим метод принятия решений, предполагающий построение множества недоминируемых альтернатив на основе нечеткого отношения предпочтения [З].
Постановка задачи в краткой форме представляется следующим образом. Пусть задано множество альтернатив А и каждая альтернатива характеризуется несколькими критериями качества с номерами j == i, ..., т. Информация о попарном сравнении альтернатив по каждому критерию качества j представлена в форме отношения предпочтения Rj. Таким образом, имеется т отношений предпочтения Rjна множестве А. Требуется выбрать лучшую альтернативу из множества {A, R1, ...,Rm}.
Метод многокритериального выбора альтернатив на основе нечеткого отношения предпочтения основан на ряде определений.
|
|
|
Определение 1. Нечетким отношением R на множестве А называется нечеткое подмножество декартова произведения А ´ А, характеризующееся функцией принадлежности mR: А ´ А ® [0,1]. Значение mR (a, b) этой функции понимается как степень выполнения отношения аÙb .
Определение 2. Нечетким отношением предпочтения на А называется любое заданное на этом множестве рефлексивное нечеткое отношение, функция принадлежности которого вычисляется следующим образом:
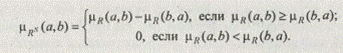
Определение 3. Пусть А — множество альтернатив и mR — заданное на нем нечеткое отношение предпочтения. Нечеткое подмножество недоминируемых альтернатив множества (А, mR) описывается функцией принадлежности
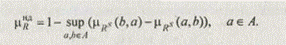
Определение 4. Четко недоминируемыми называются альтернативы, для которых mRНД (а) = 1, а множество таких альтернатив
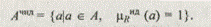
Определение 5. Носителем нечеткого множества В с функцией принадлежности mB (a) является множество {а½а Î А, mB > 0}.
Процедура решения задачи выбора выполняется в несколько шагов.
1. Строится нечеткое отношение Q1, которое является пересечением исходных отношений предпочтения:
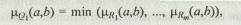
и определяется нечеткое подмножество недоминируемых альтернатив в множестве (А, mQ1):
|
|
|
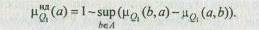
2. Строится нечеткое отношение Q2:
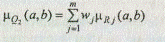
и определяется нечеткое подмножество недоминируемых альтернатив в множестве (A,mQ2):
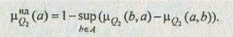
Данная функция упорядочивает альтернативы по степени их недоминируемости. Числа wj в приведенной выше свертке представляют собой коэффициенты относительной важности рассматриваемых критериев, для которых выполняются следующие условия:
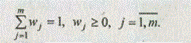
3. Отыскивается пересечение множеств mQ1НД и mQ2НД:
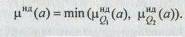
4. Рациональным считается выбор альтернатив из множества

Наиболее рациональной альтернативой из множества АНД является та, которая имеет максимальную степень недоминируемости.
Дата добавления: 2018-04-15; просмотров: 887; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
