МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ НА ОСНОВЕ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
Элементы теории нечетких множеств могут успешно применяться для принятия решений в условиях неопределенности. Основатель теории нечетких множеств Л. Заде еще в 1965 г. предрекал широкое прикладное значение своей теории, написав по этому поводу следующее: "Фактически нечеткость может быть ключом к пониманию способности человека справляться с задачами, которые слишком сложны для решения на ЭВМ".
Элементы теории нечетких множеств
Рассмотрим основные элементы теории нечетких множеств [l]. Пусть U— полное множество, охватывающее все объекты некоторого класса. Нечеткое подмножество F множества U, которое в дальнейшем будем называть нечетким множеством, определяется через функцию принадлежности mF (u), и Î U. Эта функция отображает элементы Ui, множества U на множество вещественных чисел отрезка [0,1], которые указывают степень принадлежности каждого элемента нечеткому множеству F.
Если полное множество U состоит из конечного числа элементов иi, i = 1, 2, ..., п, то нечеткое множество F можно представить в следующемвиде:
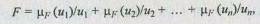
где "+" означает не сложение, а, скорее, объединение: символ "/" показывает, что значение mF относится к элементу, следующему за ним (а не означает деление на иi).
В случае, если множество U является непрерывным, F можно записать как интеграл:
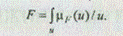
Нечеткие множества широко применяются для формализации лингвистических знаний. Рассмотрим для примера множество процентных ставок, предоставляемых банками по вкладам. Каким образом можно выделить подмножество высоких процентных ставок? В условиях динамично изменяющейся среды не всегда возможно точно ответить на этот вопрос, однозначно выделив множество высоких ставок. При использовании аппарата теории нечетких множеств решить такую задачу можно даже при отсутствии полной количественной информации об окружении. Функция принадлежности для элементов нечеткого множества F1, соответствующих понятию "высокие процентные ставки" (рис. 4.1), будет иметь следующий вид:
|
|
|
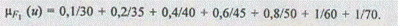
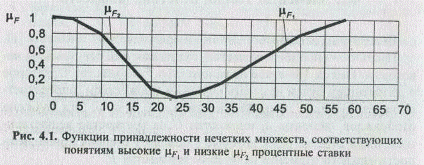
Функция принадлежности к нечеткому множеству низких процентных ставок запишется следующим образом:
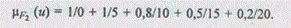
Нечеткие операции, отношения и свойства отношений
Операции над нечеткими множествами. Над нечеткими множествами, как и над обычными, можно выполнять математические операции. Рассмотрим важнейшие из них: дополнение множества, объединение и пересечение множеств.
Операция дополнения может быть представлена следующим образом:
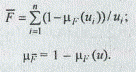
Операция объединения будет иметь следующий вид:
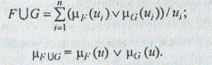
Здесь и далее операция v обозначает взятие максимума. Операция пересечения вычисляется следующим образом:
|
|
|
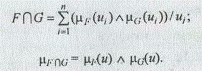
Здесь и далее символ л обозначает взятие минимума.
Нечеткие отношения. Нечетким отношением R между полным множеством U и другим полным множеством V называется подмножество прямого декартова произведения U ´ V, определяемое следующим образом:
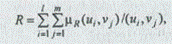
где U = {u1, u2,..., иl}, V {v1, v2,..., vm}.
Допустим, что между элементами знаний, представленных нечеткими множествами F и G, существует связь, заданная правилом: "Если F, то G", при этом F Í U, G Í V. В логике высказываний для представления правил подобного вида используется операция импликации. В нечеткой логике предложены различные способы реализации импликации. Один из наиболее простых способов заключается в представлении импликации, соответствующей правилу "Если F, то G", нечетким отношением R, которое вычисляется следующим образом [2]:
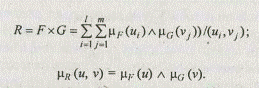
Свойства нечетких отношений.
1. Объединение отношений
(RÈ S)(u, v) = R(u, v) Ú S(u,v), и Î U, v Î V.
2. Пересечение отношений
(RÇ S)(u, v) = R(u, v) Ù S(u,v), и Î U, v Î V.
3. Операция включения
(R Í S) « R(u, v) £S (u,v), u Î U, v Î V.
4. Свойство идемпотентности
RÇR = R, RÈ R = R.
5. Коммутативность
|
|
|
RÇ S = SÇ R,RÈ S =SÈ R.
6. Ассоциативность
RÇ (SÇ Q) = (RÇ S)Ç Q.
RÈ (SÈ Q) = (RÈ SÈ Q.
7. Дистрибутивность
RÇ (SÈ Q) = (RÇ S)È (SÇ Q).
RÈ (SÇ Q) = (RÈ S)Ç (SÈQ).
8. Рефлексивность
Если mR (и, и) = 1, отношение R — рефлексивное.
Если mR (и, и) < 1, отношение R — слабо рефлексивное.
Если mR (и, и) = 0, отношение R — антирефлексивное.
Если mR (и, и) > 0, отношение R — слабо антирефлекеивное.
9. Симметричность
mR (u, v) = mR (v,и); и, v Î U.
10. Транзитивность
mR (u, v) ³ mR (u, z) Ù mR (z, v); u, v, z Î U.
Дата добавления: 2018-04-15; просмотров: 513; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
