Решение задачи методом максиминной свертки
Оценки альтернатив по заданным критериям представлены следующими нечеткими множествами:
Весовые коэффициенты важности рассматриваемых критериев определены с использованием процедуры парного сравнения и имеют следующие значения:
b = {1,78; 0,68; 0,67; 0,22; 1,65}.
Наиболее важными критериями для ЛПР являются рентабельность и инвестиционный риск, существенно менее важными — размер вложений и оценка рынков, самым меньшим весом обладает производственный риск.
Лучшая альтернатива определяется следующим образом:
Множество оптимальных альтернатив имеет вид:
mD(a) = {0,781/a1; 0,432/a2; 0,588/a3}.
Максимальное значение принадлежит а1, навтором месте находится a3, а худшей альтернативой является а2.
Решение задачи с использованием метода отношений предпочтения
На основании функций принадлежности (4.3) построены следующие отношения предпочтения на множестве альтернатив:
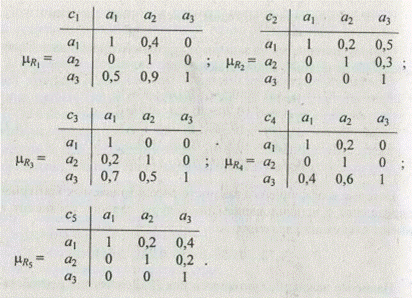
Множество недоминируемых альтернатив 
= ||1 1 1||. Значение нормированных на единицу весовых коэффициентов критериев заданы вектором w = {0,36; 0,14; 0,13; 0,05; 0,32}. Вычислим нечеткое отношение Q2:
Находим подмножество недоминируемых альтернатив множества
{А, 
}: 
(аi) = || 0,83 0,69 1 ||. Результирующее множество недоминируемых альтернатив — это пересечение множеств 
Следовательно, рациональным следует считать выбор альтернативы а3, имеющей максимальную степень недоминируемости.
|
|
|
Решение задачи с применением нечеткого логического вывода
На основании приведенных выше исходных данных о критериях и альтернативах экспертом сформулированы правила:
d1 : "Если с1 = ВЫСОКАЯ, и с2 = ХОРОШАЯ, и с3 = ПРИЕМЛЕМЫЕ, то Y = УДОВЛЕТВОРИТЕЛЬНЫЙ";
d2 : "Если c1 = ОЧЕНЬ ВЫСОКАЯ, и c2 = ХОРОШАЯ, и c3 = ПРИЕМЛЕМЫЕ, и c4 = НИЗКИЙ, и c5 = ОЧЕНЬ НИЗКИЙ,то Y = БЕЗУПРЕЧНЫЙ";
d3 : "Если c1 = НИЗКАЯ, и c2 = ПЛОХАЯ, и с3 = ВЫСОКИЙ, то Y = НЕУДОВЛЕТВОРИТЕЛЬНЫЙ".
Переменная Y задана на множестве J = {0; 0,1; 0,2; ...; 1}.
Значения переменной Y заданы с помощью следующих функций принадлежности:
S = УДОВЛЕТВОРИТЕЛЬНЫЙ, mS(x) =х,хÎ J;
US = НЕУДОВЛЕТВОРИТЕЛЬНЫЙ, mUS(x) = 1-х, x Î J. В рассматриваемой задаче оценки инвестиционныхпроектовзаданы следующими нечеткими множествами:
ВЫСОКАЯ (рентабельность) А = {0,5/а1; 0,1/а2; 1/а3};
ОЧЕНЬ ВЫСОКАЯ (рентабельность)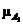 
(a) = 
(a);
НИЗКАЯ (рентабельность) 
(a) = 1 — 
(a);
ХОРОШАЯ (оценка рынков сбыта) В = {0,7/a1, 0,5/а2, 0,2/a3};
ПЛОХАЯ (оценка рынков сбыта) 
(a) = 1 - 
(a)
ПРИЕМЛЕМЫЕ (первичные средства) G = {0,3/a1, 0,5/a2,1/a3};
НИЗКИЙ (производственный риск) D = {0,5/a1, 0,3/а2, 0,9/a3};
НИЗКИЙ (инвестиционный риск) Е = {0,6/a1, 0,4/а2, 0,2/a3}
ОЧЕНЬ НИЗКИЙ (инвестиционный риск) 
(a) = 
(a);
|
|
|
ВЫСОКИЙ (инвестиционный риск) 
(a) = 1- 
(a).
Дополнительные градации лингвистических оценок (со словом ОЧЕНЬ) предназначены для учета наиболее важных критериев. В данном случае это рентабельность (c1) и инвестиционный риск (c5).
С учетом введенных обозначений правила d1, ..., d3 принимают вид:
Функции принадлежности 
для левых частей приведенных правил имеют вид:
Правила приобретут следующий вид:
Используя для преобразования правил импликацию Лукасевича, получим нечеткие отношения D1, ... D3 на U x J и в результате их пересечения функциональное решение D:
Для альтернатив вычислены следующие точечные оценки:
F(a1) = 0,500; F(a2) = 0,431; F(a3) = 0,600. Максимальную оценку имеет третья альтернатива, следовательно, она является наиболее предпочтительной.
Дата добавления: 2018-04-15; просмотров: 1891; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!