Понятие «итерационный (приближенный) численный метод.
Это приближённый метод. Он позволяет получить решение сис-темы линейных алгебраических уравнений с погрешностью, не превышающей заданную допустимую величину ε, за ограниченное количество итераций.
При этом может быть достигнута экономия машинного времени по сравнению с получением точного решения по методу Гаусса, требующему больших трудозатрат, резко возрастающих с увеличением порядка решаемой системы уравнений.
Имеем исходную систему уравнений:
(1.5)
Запишем систему (1.5) в матричной форме:
AX = B, (1.6)
где A (n´n) – матрица коэффициентов aij;
B(n) – вектор правых частей bi;
X(n) – вектор решений xj.
Можно представить исходную систему матричным уравнением
AX – B = 0 (1.7)
или в развёрнутой матричной форме
(1.8)
Вектор-столбец в правой части с нулевыми значениями элементов получается, когда векторX есть точное решение системы. В противном случае получим вектор-«невязок» Δx.
Обозначим через Z вектор приближённых значений решения системы. Вначале это будет нулевое приближение – вектор Z(0). В качестве начального приближения решения системы можно брать 
.
При подстановке в систему (1.8) на место X вектора Z(0) получим:
(1.9)
|
|
|
где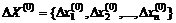 
– вектор-«невязок» начального (нулевого) приближения относительно точного решения.
Цель и суть метода простых итераций – сведение к нулю «невязок» в решении системы (1.9). Практически стремятся к выполнению условия
(1.10)
где S – номер итерации, S = 0, 1, 2, …
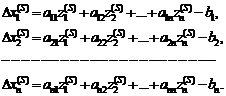
Величина 
получается из соответствующего i-го уравнения системы (1.9).
Общая формула
(1.11)
где j – номер слагаемого скалярного произведения i-той строки матрицы A на вектор Z.
Если хотя бы по одному условие (1.10) не выполняется, то производится корректировка начального и любого предыдущего приближения к точному решению, и получается новое приближение:
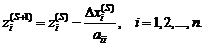(1.12)
Значение aii не равно нулю, что следует из условия сходимости.
Далее на следующей итерации вычисляются новые значения «невязок» 
.
Если для всех «невязок» условие (1.10) выполняется, то формируется вектор приближённых решений системы (1.1):
(1.13)
Условие сходимости метода простых итераций
Метод простых итераций сходится при условии, что диагональные коэффициенты матрицы A исходной системы по абсолютной величине больше суммы абсолютных величин других коэффициентов в своей строке:
|
|
|
Чем больше преимущество (доминирование) диагональных коэффициентов в своей строке (в этом случае говорят, что матрица хорошо обусловлена), тем меньше потребуется итераций для получения решения системы с той же точностью.
Трудоёмкость метода простых итераций
Количество действий этого метода на одной итерации
Qитер = 2n2 + 5n.
Однако надо иметь в виду, что решение по этому методу получается после выполнения нескольких итераций. Количество их зависит от требуемой точности.
Решение ОДУ модифицированным методом Эйлера: порядок точности, начальные условия, расчетная формула для получения решения, графическая интерпретация, вычисление погрешности по правилу Рунге.
В данном методе мы находим tg угла наклона касательной в точке:
x = x[m] + h/2; y = y[m] + (h/2)*y'[m]
Соотношения, описывающие модифицированный метод Эйлера имеют вид:
y[m+1] = y[m] + h*F(x[m],y[m],h) (7)
F(x[m],y[m],h) = f( x[m]+h/2, y[m]+(h/2)*y'[m] ) (8)
y'[m] = f(x[m],y[m]) (9)
Модифицированный метод Эйлера также согласуется с разложением в ряд Тейлора вплоть до членов степени h^2, и также является методом Рунге-Кутта второго порядка.
|
|
|
Дата добавления: 2018-04-15; просмотров: 454; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!