Понятие «численный метод эквивалентных преобразований».

⇐ ПредыдущаяСтр 10 из 12Следующая ⇒

Методы эквивалентных преобразований – это методы, позволяющие заменить исходную задачу другой, имеющей то же решение. Выполнение эквивалентных преобразований оказывается полезным, если новая задача проще исходной, или обладает лучшими свойствами, или для неё существует известный метод, а может быть, и готовая программа.

31.Понятие «численный метод аппроксимации (приближения)».

Понятие «аппроксимация» происходит от латинского «appro-ximo» – приближаюсь. Задача аппроксимации состоит в приближённом выражении одних величин или геометрических образов через другие более простые.

Существует два основных подхода к аппроксимации табличных данных непрерывными функциями.

1.При одном из них требуется, чтобы аппроксимирующая функция в узлах аппроксимации имела значения, равные табличным. Этого удается достичь с помощью методов интерполяции.

2.При другом подходе табличные данные аппроксимируют простой функцией, применимой во всем диапазоне данных, нонеобя-зательно совпадающей в узлах аппроксимации с табличнымизначе-ниями. При этом обычно стремятся свести к минимуму сумму квадратов отклонений.

Интерполяция данных осуществляется след ми методами: Метод Лагранжа,Метод Ньютона,Интерполяция с помощью сплайнов.методом наименьших квадратов.

32.Решение ОДУ обыкновенным методом Эйлера: порядок точности, начальные условия, расчетная формула для получения решения, графическая интерпретация, вычисление погрешности по правилу Рунге.

Дано ОДУ y′ = f(x, y), начальное условие x = x₀, y = y₀. Диффе-ренциальное уравнение графически задаёт наклон кривой решения y = y(x) в любой точке x, а физически характеризует скорость изме-нения функции y = y(x). В начальный момент известна точка x₀, y₀. В этой точке вычисляем по заданному дифференциальному уравне-нию производную функции y′ = f(x₀, y₀) и, принимая на шаге h эту величину постоянной, переходим в точку x₁ = x₀ + h, где получаем новое значение y₁ = y₀ + hf(x₀, y₀). Эту процедуру продолжаем дальше.

Расчётная формула метода Эйлера

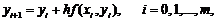
где m – количество точек решения.

Графическая интерпретация метода Эйлера дана на рис. 1.14.

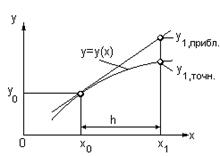
Рис. 1.14

Оценим погрешность метода Эйлера. Для этого разложим точ-ное решение в окрестности h от точки x_i в ряд Тейлора

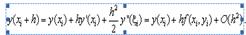Это разложение согласуется с формулой метода Эйлера до чле-нов первого порядка по h, а погрешность метода равна остаточному члену

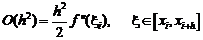Если расчётная формула численного метода согласуется с раз-ложением в ряд Тейлора до членов порядка 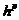, то число p называется порядком точности метода.

Таким образом, метод Эйлера является методом первого поряд-ка точности (p = 1).

Практическая оценка погрешности метода Эйлера может быть получена по правилу Рунге

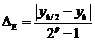где y_h, y_h_/2 – решения дифференциального уравнения, полученные на каждом отрезке интегрирования за один шагh и за два половинных шага h / 2.

При p = 1 получаем .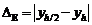

34. Решение ОДУ исправленным методом Эйлера: порядок точности, начальные условия, расчетная формула для получения решения, графическая интерпретация, вычисление погрешности по правилу Рунге

В исправленном методе Эйлера мы находим среднийtg угла наклона касательной для двух точек: x[m],y[m] и x[m+1],y[m]+h*y'[m]. Соотношения, описывающие данный метод, имеют вид:

y[m+1] = y[m] + h*F(x[m],y[m],h) (4)

F(x[m],y[m],h) = ( y'[m] + f(x[m]+h, y[m]+h*y'[m]) )/2 (5)

y'[m] = f(x[m],y[m]) (6)

Исправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h^2, являясь, т.о. методом Рунге-Кутта второго порядка.

Дата добавления: 2018-04-15; просмотров: 394; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 7 8 91011 12 Следующая ⇒

Мы поможем в написании ваших работ!