II. Общее уравнение плоскости

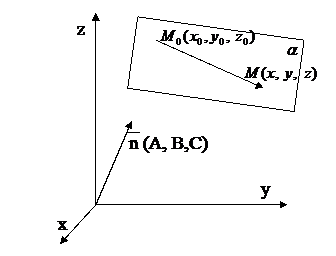
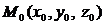Пусть плоскость проходит через точку перпендикулярно вектору .

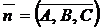Этими условиями определяется единственная плоскость в пространстве 0xyz.

Вектор 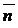называется нормальным вектором плоскости .

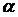Чтобы получить уравнение плоскости 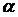, возьмем в плоскости 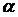точку 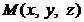. Тогда вектор 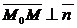, а значит, их скалярное произведение равна нулю, т.е. .

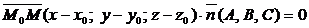Отсюда получаем уравнение вида

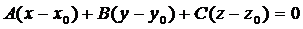
которое называют уравнением плоскости, проходящей через данную точку 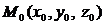перпендикулярно вектору.

Выполнив преобразования в этом уравнении и заменив 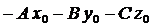на D, получим уравнение вида

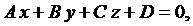
которое называют общим уравнением плоскости.

III. Виды уравнения плоскости в пространстве

В пространстве с заданной декартовой системой координат однозначное расположение плоскости можно задать различными способами, соответственно существуют различные уравнения плоскости в пространстве.

Уравнение плоскости, проходящей через три заданные точки

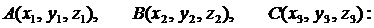
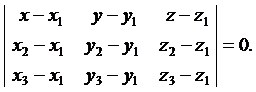(1)

Здесь x, y, z – текущие координаты точки плоскости.

1. Уравнение плоскости, проходящей через заданную точку 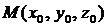перпендикулярно заданному вектору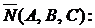

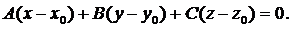(2)

2.Если в уравнении (2) раскрыть скобки и обозначить свободный член через D , получим общее уравнение плоскости:

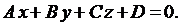(3)

Если в общем уравнении (3) один из коэффициентов А, В, С равен нулю, то плоскость проходит параллельно соответствующей оси. Если два коэффициента из А, В, С равны нулю, плоскость параллельна одной из координатной плоскости.

Например, плоскость 4x-5z-1= 0 проходит параллельно оси 0у,

плоскость у+3= 0 проходит параллельно координатной плоскости х0у через точку у = - 3 на оси 0у.

Коэффициенты А, В, С в общем уравнении плоскости являются одновременно координатами вектора, перпендикулярного плоскости.

4. Разделив уравнение (3) на (-D), получим уравнение плоскости в отрезках:

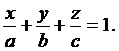                                                                          (4)

Здесь a, b, c – отрезки, отсекаемые плоскостью на осях координат.

Например, плоскость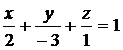

пересекает оси координат в точках x = 2, y = -3, z = 1.

IV. Прикладные задачи в пространстве

Также, по аналогии с аналитической геометрией на плоскости, возможно решение следующих прикладных задач:

2.Расстояние d от точки 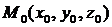в пространстведо плоскости Р, заданной уравнением (3), определяется по формуле:

3.

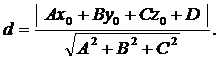                                                      (5)

4.Две плоскости перпендикулярны (параллельны) друг другу, если перпендикулярны (параллельны) их векторы-нормали. Поэтому, если даны две плоскости





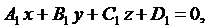
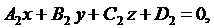
то:

условие перпендикулярности плоскостей:



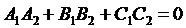
условие параллельности плоскостей:

                                 .

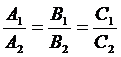3. Косинус угла между двумя плоскостями, заданными общими уравнениями 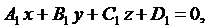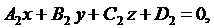находят по формуле:

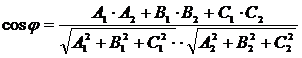
Пример:

Даны: четыре точки М₁(1, -1, -1), М₂(2, 1, 3), М₃(0, 1, -1), М₀(6, 8, 2). Требуется:

а) написать уравнение плоскости, проходящей через точки М₁, М₂ М₃ ;

б) преобразовать полученное уравнение плоскости Р в уравнение плоскости в отрезках и построить её ;

в) найти расстояние d от точки М₀ до плоскости Р.

Решение:

а) Подставим координаты точек М₁, М₂ М₃ в уравнение (1):

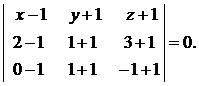
Раскрыв определитель, получим:

-8х-4у+4z+8=0 .

Разделим на (-4) и получим окончательное общее уравнение искомой плоскости Р:

2x+y-z-2=0 .

б) Перенесем свободный член в правую часть и, разделив на него обе части уравнения, получим уравнение плоскости в отрезках:

.

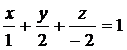Откладываем отрезки a=1; b=2; ç= -2 на осях 0x, 0y, 0z соответственно и строим плоскость Р (см. рис.)

в) Расстояние d от точки М₀ до плоскости Р найдем по формуле (5):

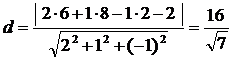                                 (ед. длины).

Дата добавления: 2018-04-05; просмотров: 463; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!