Основные свойства кватерниона
Сумма кватернионов
.
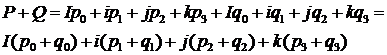Как следствие, можем записать свойство коммутативности
.
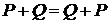и свойство ассоциативности
.
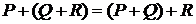2.Разность кватернионов
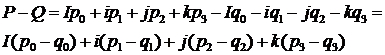
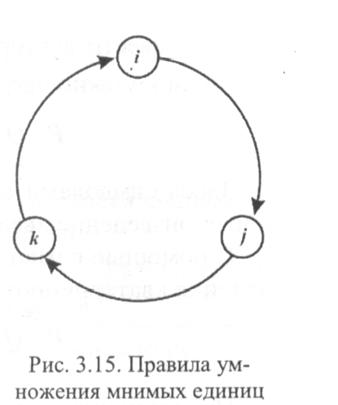
Произведениеобозначается символом«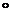 
»и определяется правилами перемножения мнимых единиц
, 
, 
, 
, 
, 
,
, 
, 
.
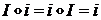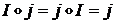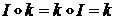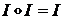
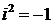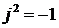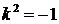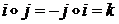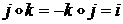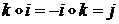Пример. Найти произведение двух кватернионов
, 
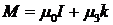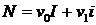
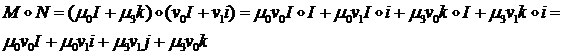
Можно показать, что если ввести в рассмотрение векторы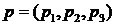 
и 
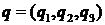, то произведение кватернионов представимо в виде
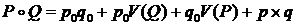
Можно также показать, что
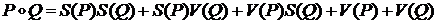
Как следствие также может быть записано
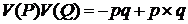
где правая часть содержит как скалярное, так и векторное произведение векторов.
Сопряженное произведение кватернионов
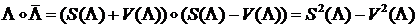
Так как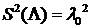 
,
,
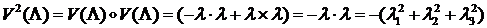то
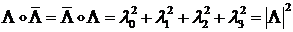
Число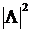 
называется нормой кватерниона и обозначается как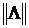 
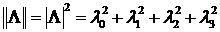
Произведение кватернионов, имеющих нулевые скалярные части
При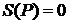 
, 
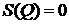имеем
.
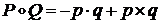
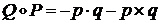Тогда
/
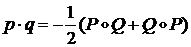
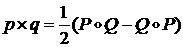Обратный кватернион
Обратный кватернион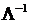 
определяется из условия
.
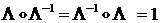Умножая справа это выражение на сопряженный кватернион, получим
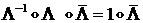
С учетом ассоциативности имеем
.
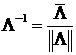Для нормированного кватерниона имеют место соотношения
, 
.
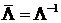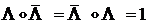Собственные кватернионы
-это кватернионы с параметрами Родрига-Гамильтона. Так как эти параметры связаны соотношением
,
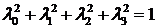то собственный кватернион является нормированным.
Найдем кватернионы для последовательности поворотов на угол рыскания , тангажа и крена.
Первый поворот на угол рыскания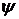 
(см. рисунок). Осью конечного поворота 
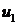является ось 
.
|
|
|
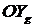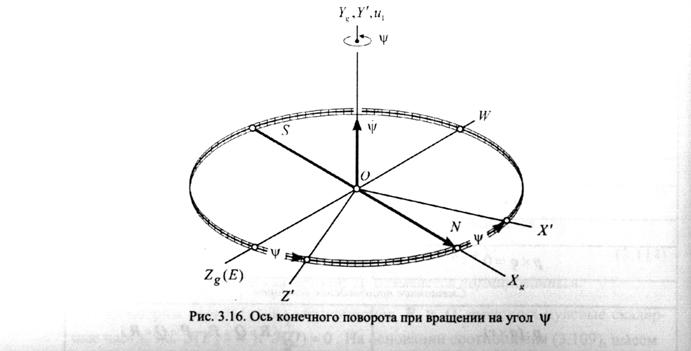
Найдем направляющие косинусы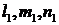 
,
,
,
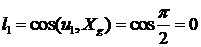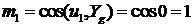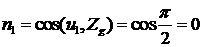и параметры Родрига- Гамильтона
, 
, 
, 
.
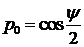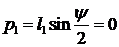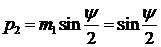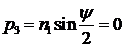Совокупности этих параметров поставим в соответствие собственный кватернион
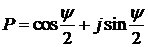
Аналогично могут быть получены кватернионы для других поворотов
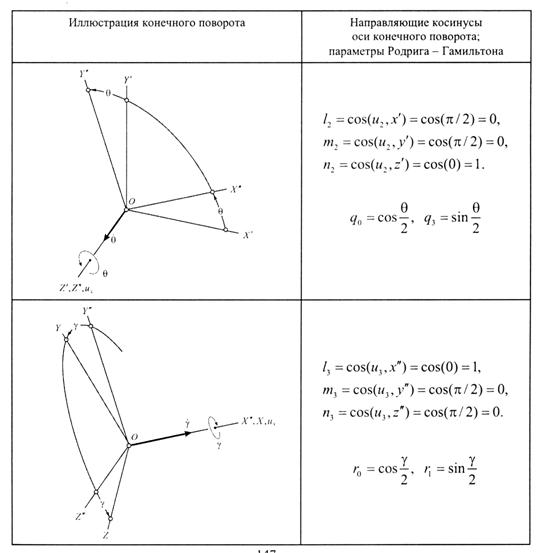
и могут быть записаны кватернионы
, 
.
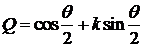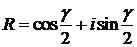Для того, чтобы определить результирующий кватернион
,
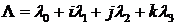характеризующий взаимное положение системы координат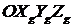 
и 
необходимо найти произведение
.
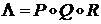Можно показать, что параметрами кватерниона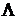 
будут параметры
,
,
,
.
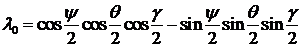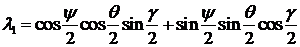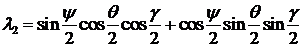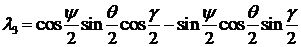Рассмотрим . как преобразуются компоненты некоторого вектора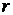 
при переходе от системы координат 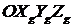к системе .
.
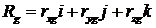
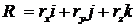Кватернионы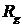 
и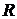 
называются гиперкомплексными отображениямивектора 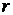на базисы 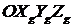и .
Если переход от системы координат 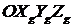в системе осуществляется с использованием кватерниона 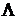, то имеет место следующее равенство
,
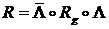называемое равенством перепроектирования
Умножая это равенство справа на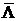 
, с учетом нормированности кватерниона можно также получить равенство
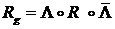
Кинематические уравнения для кватерниона
Заменим векторное уравнение линейной скорости объекта
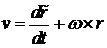
его кватернионным аналогом
|
|
|
, (*)
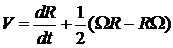где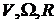 
-гиперкомплексные отображения вектора абсолютной линейной скорости 
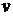, вектора угловой скорости 
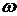и вектора .
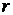Пусть переход от неподвижной системы координат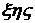 
к подвижной 
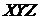осуществляется кватернионом 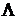. Тогда преобразование компонент вектора 
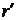из системы в компоненты вектора в системе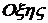 
подчиняется обратному равенству перепроектирования
.
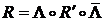Дифференцируя обе части уравнения получим
.
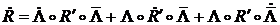Умножая слева на кватернион 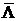получим
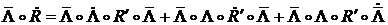
откуда
. (**)
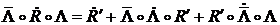В этом уравнении величина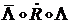 
есть абсолютная линейная скорость 
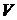, поэтому левые части равны
Получим
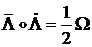
или
.
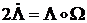Это уравнение и является кинематическим уравнением для кватерниона
Решая это уравнение , представленное в скалярном виде можно определить параметры Родрига –Гамильтона, через проекции угловой скорости , при этом эти параметры характеризуют положение подвижной системы координат относительно неподвижной .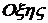
Дата добавления: 2018-04-05; просмотров: 1277; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!