БИНС с направляющими косинусами
Уравнение Пуассона
Одним из распространенных параметров ориентации являются направляющие косинусы
Определение направляющих косинусов через углы последовательных поворотов операция достаточно трудоемкая. Поэтому направляющие косинусы чаще используются в качестве самостоятельных параметров ориентации, поскольку они могут быть вычислены аналитически если известны их начальные значения и угловые скорости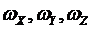 
с которой система 
вращается вокруг системы 
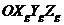Если матрица преобразования известна
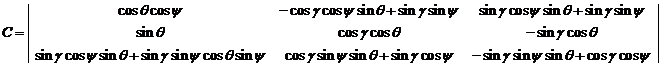
то углы рыскания тангажа и крена могут быть определены через элементы этой матрицы
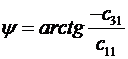
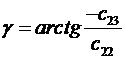
Из теоретической механики известно, что дифференцирование вектора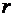 
, определяющего координаты кочек в некоторой системе координат (координаты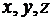 
) дает линейную скорость
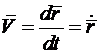
с проекциями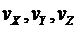 
на оси .
Если эта система вращается относительно некоторой неподвижной системы координат 
, то абсолютная линейная скорость точки определяется как
(*)
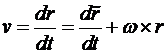В правой части этого равенства обозначение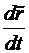 
представляет собой скорость точки в системе координат , а второе учитывает факт вращения 
этой системы относительно неподвижной системы координат . Векторному уравнению (*) соответствуют три скалярных уравнения
.
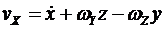
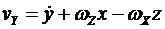
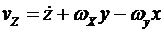В матричной форме эти уравнения можно записать как
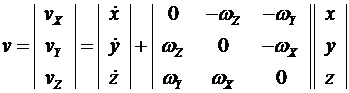
Координаты точки в подвижной и неподвижной системах координат связаны матричной зависимостью
|
|
|
,
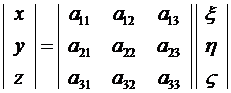которая характеризует преобразование координат, т.е переход от координат точки в неподвижной системе координат к координатам той же точки в подвижной системе координат.
При обратном переходе от координат точки в системе к координатам в системе используется матрица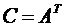 
.
Соответствующее преобразование координат выражается зависимостью
(**)
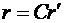где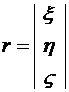 
, 
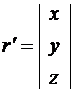
Для установления связей направляющих косинусов с угловыми скоростями 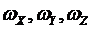, с которой подвижная система вращается относительно неподвижной продифференцируем по времени это выражение
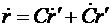
Умножим это выражение слева на матрицу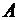 
.
.
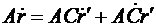Учитывая, что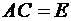 
, получим
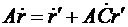
В этом уравнении левая часть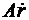 
представляет собой абсолютную линейную скорость точки 
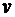в подвижной системе координат вследствие чего уравнения
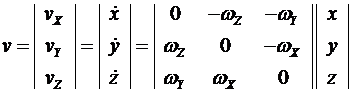и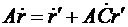
эквивалентны.
Из их сравнения следует, что
,
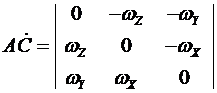или
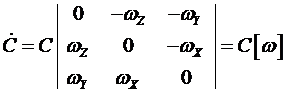
Аналогичное уравнение можно записать также относительно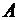
.
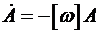Последнее уравнение в инерциальной навигации известно как уравнение Пуассона, связывающее производную от матрицы направляющих косинусов с самой матрицей и вектором угловой скорости с которыми система вращается относительно неподвижной системы координат .
|
|
|
Таким образом, направляющие косинусы могут быть определены через решение этого дифференциального уравнения.
Матричное уравнение эквивалентно девяти скалярным уравнениям
, 
, 
,
, 
, 
,
, 
, .
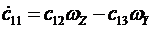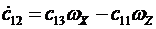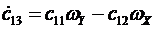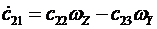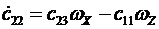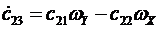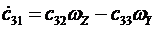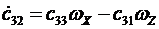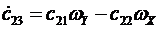Скалярный вид уравнений Пуассона показывает, что совокупность этих уравнений распадается на три отдельно интегрируемые системы из трех уравнений. Первая триада имеет переменные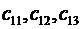 
, вторая- 
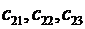, третья 
.
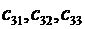Дата добавления: 2018-04-05; просмотров: 1360; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!