Комбінаційні арифметичні вузли 1 страница

 

7.3.1. Загальна характеристика арифметичних вузлів. Арифметично-логічний пристрій (АЛП) процесора виконує арифметичні і логічні операції над багаторозрядними двійковими словами. До складу АЛП входять блоки призначені для виконання арифметичних операцій над числами в форматах з фіксованою крапкою, плаваючою крапкою та десятковому форматі. Важливою частиною цих блоків є цифрові вузли, що виконують елементарні математичні операцій: додавання, віднімання, множення, ділення і порівняння двійкових чисел. Такі вузли будують на основі логічних елементів, як комбінаційні схеми, тому вони мають назву комбінаційні арифметичні вузли.

Особливістю двійкової арифметики є те, що чотири арифметичні дії в ній можна звести до двох операцій - додавання і зсуву. Тому основу арифметичних вузлів складають суматори. Суматором називають функціональний вузол комп’ютера, призначений для додавання двох n-розрядних двійкових слів (чисел). Такі вузли будують на базі елементарних цифрових вузлів, здатних виконувати операцію додавання в одному розряді двійкового числа, тобто додавати два однобітових числа. До таких однорозрядних арифметичних вузлів відносяться напівсуматор і повний суматор

За способом додавання суматори поділяють на паралельні, послідовні та паралельно-послідовні. У паралельних n-розрядних суматорах значення всіх розрядів операндів надходять у паралельному коді одночасно на відповідні входи суматора, кількість яких визначає розрядність двійкових чисел, що додаються. Послідовні суматори виконують операцію додавання операндів представлених у послідовному коді. Для виконання операції додавання вони використовують один однорозрядний суматор, на входи якого, в кожному  такті, поступають  значення розрядів  операндів послідовно в напрямку від молодших розрядів до старших, а перенесення, що запам’ятовується у попередньому такті за допомогою тригера, враховується при формуванні значення однорозрядної суми в поточному такті. Складовою частиною послідовних n-розрядних суматорів є регістри зсуву, тому такі суматори не є комбінаційними цифровими вузлами. В паралельно-послідовних суматорах n-розрядні числа розбиваються на частини по k розрядів. Кожна з цих частин подається у паралельному коді на входи k-розрядного суматора (одночасно у всіх розрядах), а самі частини – послідовно, роздільно у часі, в напрямку від молодших частин до старших з урахуванням перенесення, яке запам’ятовується.

За схемотехнічними ознаками і особливостями формування результату операції додавання суматори поділяють на комбінаційні і накопичувальні. Комбінаційні суматори не містять елементів пам’яті і реалізуються, як комбінаційні схеми. Накопичувальні суматори являють собою поєднання комбінаційного суматора і регістра. Такі суматори працюють згідно співвідношенню S := S+A („:=” – символ присвоювання), тобто до попереднього значення суми S, що зберігається у регістрі, додається черговий доданок А і результат заміщає старе значення суми у регістрі.

За способом організації перенесення між розрядами суматори поділяють на суматори з послідовним, паралельним, наскрізним та груповим перенесеннями. Спосіб перенесення визначає час виконання операції додавання. Суматори з послідовним перенесенням схемотехнічно організовані досить просто, але мають низьку швидкодію порівняно з суматорами з паралельним перенесенням, які схемотехнічно організовані значно складніше.

За системою числення суматори поділяють на двійкові і десяткові. Двійкові суматори виконують операцію складання двійкових операндів представлених у знаковому і беззнаковому форматі з фіксованою крапкою (див. підрозділ 7.2.8). В десяткових суматорах для подання операндів використовується двійково-десятковий код (див. підрозділ 1.2). Такі суматори будують з урахуванням правил десяткової арифметики на основі двійкових суматорів, які виконують операцію додавання двійкових тетрад, які відображують десяткові цифри в двійково-десятковому коді.

При побудові арифметичних вузлів комп’ютера на основі двійкових суматорів враховують, що операція віднімання може бути замінена додаванням двійкових операндів у оберненому або доповняльному коді, а операції множення та ділення можна звести до багаторазового додавання та зсування. Отже розглянемо принципи побудови арифметичних вузлів комп’ютерної електроніки.

7.3.2. Однорозрядні двійкові суматори. Такі суматори виконують додавання однорозрядних двійкових чисел. В залежності від можливості враховувати перенесення в результаті операції їх поділяють на напівсуматор і повний суматор.

	A B S P 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1
а	б
Рис. 7.29.  Напівсуматор:  умовне графічне зображення (а); таблиця справжності (б)

Напівсуматор не враховує перенесення. Він має два входи на які подаються однорозрядні операнди A і B та два виходи, на яких формується сума S і значення перенесення P. Такий елементарний суматор при побудові багаторозрядних суматорів може бути використаним тільки у молодшому розряді, де перенесення відсутнє. Умовне графічне зображення напівсуматора і його таблиця справжності, побудована з урахуванням правил двійкової арифметики, наведені на рис. 7.29. З таблиці справжності випливає, що функції виходів напівсуматора S і P описують логічні рівняння:

                     S = B + A 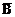 = AÅB; P = AB.   (7.34)

Схеми напівсуматора в булевому базисі і базисі Жегалкіна, побудовані на підставі (7.34), показані на рис. 7.30.

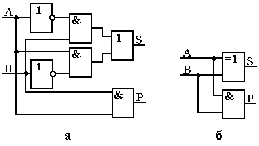
Рис. 7.30. Схеми напівсуматора в булевому базисі (а) та базисі Жегалкіна (б)

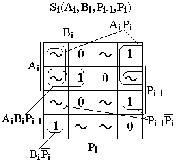
Повний суматор враховує перенесення, тому має три входи: А і B для однорозрядних операндів і вхід перенесення P₀. Як й напівсуматор, повний суматор на двох своїх виходах формує значення суми S і перенесення P від операції додавання, яку він виконує. Умовне зображення повного суматора показано на рис. 7.31а. Завдяки здатності враховувати перенесення повний суматор при побудові на його основі n-розрядних суматорів може бути використаний у будь-якому i-тому розряді такого суматора. В цьому випадку функції виходів повного суматора i-того розряду S_i і P_i залежать від значення розрядів A_i, B_i багаторозрядних операндів і значення перенесення P_i-1 з сусіднього молодшого i-1-го розряду (рис. 7.31а).

	Ai Bi Pi-1 Pi Si 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 1 0 1 1 1 0 1 1 0 1 0 0 1
а	б
Рис. 7.31. Повний суматор: умовне графічне зображення (а); таблиця справжності (б)

Таблиця справжності для функцій P_i(A_i,B_i,P_i-1), S_i(A_i,B_i,P_i-1), побудована з урахуванням правил двійкової арифметики, наведена на рис. 7.31б, а результати мінімізації методом Вейча показані на рис. 7.32а. З них випливає, що склеювання одиниць має місце тільки для функції P_i(A_i,B_i,P_i-1). Її логічне рівняння, отримане за результатами склеювання, має вигляд:

                           P_i = A_iB_i + B_iP_i-1 + A_iP_i-1,        (7.35)

а логічне рівняння для функції виходу S_i повного суматора у ДДНФ можна записати як

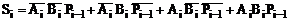     . (7.36)

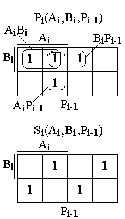
а	б
Рис. 7.32. Результати мінімізації методом Вейча функцій виходів повного суматора (а) і функції його виходу S, як булевої функції чотирьох змінних (б)

Із співвідношень (7.35), (7.36) випливає, що для побудови схеми повного суматора в булевому базисі потрібні 3 інвертори, чотири елемента 3І, три елемента 2І, один елемент 4АБО і один 3АБО, тобто всього 12 елементів. Схему повного суматора можна спростити, скоротивши кількість логічних елементів, якщо виконати мінімізацію S_i, розглянувши цю функцію як частково визначену БФ чотирьох змінних S_i(A_i,B_i,P_i-1,P_i). Результати такої мінімізації представлені на рис. 7.32б. З них випливає наступне логічне рівняння:

                 .  (7.37)

В цьому випадку, з урахуванням (7.35), для побудови схеми повного суматора потрібен тільки один інвертор, шість елементів 2І, один 3І, один елемент 4АБО і один 3АБО, тобто всього 10 логічних елементів. Така схема наведена на рис. 7.33. Її особливістю є наявність зворотного зв’язку між виходом перенесення P_i і схемою формування однорозрядної суми S_i. Наслідком цього є те, що швидкодія формування суми менша за швидкодію формування перенесення, оскільки час затримки сигналу P_i визначається тільки сумою затримок поширення сигналу елемента І та АБО, а час затримки формування суми S_i - сумою затримок перенесення P_i і поширення сигналу в логічних елементах НЕ, І та АБО. Тому параметри швидкодії повного суматора визначаються співвідношеннями:

           t_зпP = t_зпI + t_зпАБО; t_зпS = 2t_зпI + 2t_зпАБО + t_зпНЕ. (7.38)

Рис. 7.33. Схема повного суматора в булевому базисі

7.3.3. Багаторозрядні двійкові суматори. Розглянуті вище однорозрядні суматори використовують для побудови багаторозрядних суматорів, призначених для додавання n-розрядних двійкових чисел, які будемо позначати як: А = A_nA_n-1…A_i…A₂A₁, B = B_nB_n-1…B_i…B₂B₁. Звичайно такі суматори будують на основі повних суматорів, що дозволяють враховувати у сумі поточного розряду перенесення із сусіднього молодшого розряду. Для побудови n-розрядного паралельного суматора, очевидно, потрібно n однорозрядних повних суматорів.

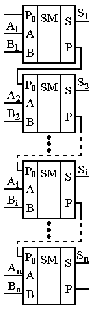
Найпростішим за схемотехнічною організацією є паралельний суматор з послідовним перенесенням, схема якого та умовне зображення показані на рис. 7.34.

Значення всіх розрядів чисел A і B поступають на входи відповідних однорозрядних суматорів одночасно, а сигнал перенесення передається від розряду до розряду послідовно у часі, починаючи від молодшого розряду суми S₁ до її старшого розряду S_n.

У паралельних суматорах з послідовним перенесенням час виконання операції складання t_S у найгіршому випадку, коли сигнал перенесення послідовно розповсюджується від першого до n-того розряду, визначається співвідношенням:

                                   t_S = (n-1)t_зпP + t_зпS,          (7.39)

де значенням t_зпP і t_зпS для повних суматорів реалізованих за схемою на рис. 7.33 задаються співвідношеннями (7.38).

а	б
Рис. 7.34.  Схема паралельного суматора з послідовним перенесенням (а) і умовне зображення n-розрядних суматорів(б)

Коли кількість розрядів n паралельних суматорів з послідовним перенесенням зростає їх швидкодія зменшується. Це недолік таких суматорів. Для підвищення швидкодії в суматорах застосовують схеми прискореного - паралельного перенесення, тому такі суматори називають паралельними суматорами з паралельним перенесенням.

Схеми прискорених переносів виробляють сигнали перенесення P_i одночасно для всіх розрядів суматора. Сигнал P_i для даного розряду формується такими схемами з урахуванням всіх змінних необхідних для вироблення перенесення, тобто тих, від яких залежить його наявність або відсутність. Такими змінними є зовнішнє перенесення P₀ та значення всіх розрядів доданків, які є молодшими відносно даного розряду. З урахуванням цього структура n-розрядного суматора з паралельним перенесенням має вигляд, показаний на рис. 7.35. Тут схеми прискорених переносів позначені як CR (від англійського слова carry - перенесення), а для повних суматорів SM вихід переносу не показаний, оскільки він не приймає участі у формуванні значення суми.

Для визначення логічної структури схем прискореного переносу CR_i використовують дві допоміжні функції: генерації і прозорості.

Функція генерації приймає одиничне значення, коли перенесення на виході даного розряду з’являється незалежно від наявності або відсутності вхідного перенесення. Це має місце колі обидва доданки A_i і B_i дорівнюють одиниці, тому функцію генерації можна представити кон’юнкцією g_i = A_i×B_i.

 

Рис. 7.35. Структура суматора з паралельним перенесенням

Функція прозорості приймає одиничне значення, коли перенесення в даному розряді з’являється тільки при наявності сигналу перенесення на вході повного суматора цього розряду. Це має місце, коли хоча б один з доданків A_i чи B_i приймає одиничне значення, тобто функцію прозорості можна представити у вигляді виключального АБО (суми за модулем 2) h_i = 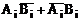 = A_i Å B_i. Аналіз можна спростити, якщо виключальне АБО замінити диз’юнкцією, тобто функцію прозорості записати у вигляді h_i = A_i + B_i. Підставою для такої заміни є те, що перенесення буде виникати і у випадку, коли обидва доданки дорівнюють одиниці.

З урахуванням викладеного вище вираз для функції перенесення P_i в будь-якому i-тому розряді суматора можна записати у вигляді:

                                     P_i = g_i + h_iP_i-1.               (7.40)

На підставі (7.40) для функцій перенесення різних розрядів суматора можна отримати наступну систему рівнянь:

P₁ = g₁ + h₁P₀;

P₂ =g₂ +h₂(g₁ + h₁P₀) = g₂ +h₂g₁ + h₂h₁P₀;

P₃ = g₃ + h₃(g₂ + h₂(g₁ + h₁P₀)) =

= g₃ + h₃g₂ + h₃h₂g₁ + h₃h₂h₁P₀;

 

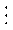                                                                               (7.41)

 

P_i = g_i + h_ig_i-1 + h_ih_i-1g_i-2 + h_ih_i-1h _i-2g_i-3 +…+h_ih_i-1…h₂g₁ +

+h_ih_i-1…h₂h₁P₀,

де P₀ – значення вхідного перенесення суматора.

Побудову схеми суматора з паралельним перенесенням розглянемо на прикладі чотирьохрозрядного суматора. Функції перенесення такого суматора описуються першими трьома рівняннями системи (7.41). На підставі закону де Моргана приведемо ці рівняння до базису І-НЕ:

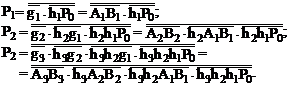     (7.42)

На рис. 7.36 показано варіант схеми паралельного суматора з паралельним перенесенням, яка побудована згідно (7.42), з урахуванням, що h_i = A_i + B_i (i = 1, 2, 3).

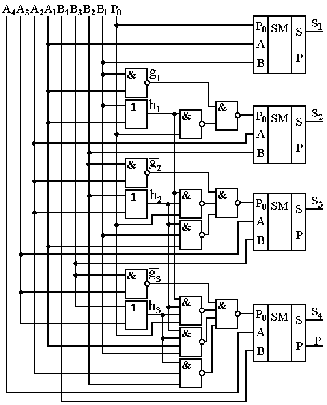
Рис. 7.36. Схема чотирьохрозрядного суматора з паралельним перенесенням

Хоча кількість логічних елементів схеми прискореного перенесення зростає в старших розрядах суматора, в будь-якому розряді вона має три рівня затримки. Це означає, що на відміну від суматора з послідовним перенесенням значення бітів суми формуються одночасно для всіх двійкових розрядів, тому час виконання операції складання t_S не залежить від кількості розрядів суматора і визначається співвідношенням:

                                     t_S = 3t_зп + t_зпS,               (7.43)

де t_зп - час затримки поширення сигналу логічних елементів АБО та І-НЕ схеми прискореного перенесення (для спрощення прийнято, що ці елементи мають однакову затримку поширення сигналу, яка дорівнює t_зп), t_зпS – час затримки поширення повного суматора.

Отже перевагою суматорів з паралельним перенесенням є висока швидкодія, що не залежить від кількості розрядів суматора. Недолік полягає в ускладненні схеми, порівняно з суматорами з послідовним перенесенням (рис. 7.34а). Окрім того із зростанням кількості розрядів суматора, зростає кількість входів логічних елементів І-НЕ схеми прискореного перенесення, а оскільки вона обмежена значенням K_об = 8, суматори, побудовані за схемою, яка наведена на рис. 7.36, не можуть мати більше восьми розрядів. При побудові суматорів з більшою розрядністю використовують комбіноване паралельно-послідовне перенесення.

---

Дата добавления: 2018-04-05; просмотров: 715; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!