Классификация наиболее важных статистических методов

Статистические методы сравнения 2-х выборок

Вид тестовых шкал	Вид данных	Зависимые выборки		Независимые выборки
		Параметрический	Непараметрический	Параметрический	Непараметрический
Номинальная (наименований)	Качественные: номинальные категориальные (nominal, categorical)	-	Критерий МакНемара	-	Критерий хи-квадрат Пирсона (критерий согласия)
Порядковая (ранговая, ординальная)	Качественные: порядковые, ранговые, ординальные (ordinal)	-	Критерий знаков Вилкоксона	-	U-критерий Манна-Уитни Критерий ранговых сумм Вилкоксона Критерий Колмогорова-Смирнова
Интервальная (разностей)	Количественные: дискретные (descrete), непрерывные (continious)	t-критерий Стьюдента (независимые выборки)	Критерий знаков Вилкоксона	t-критерий Стьюдента (независимые выборки)	U-критерий Манна-Уитни Критерий ранговых сумм Вилкоксона Критерий Колмогорова-Смирнова
Абсолютная (отношений)

 

Алгоритм выбора статистического критерия

- Нормальное распределение

–Параметрические методы:

- Количественные переменные: критерий Стьюдента для зависимых или независимых    выборок (ограничение по равенству дисперсий в выборках).

- Распределение, отличающееся от нормального

       -Непараметрические методы:

- Бинарные переменные:

       - ожидаемые значения менее 5 – тест Фишера (параметр.).

       - ожидаемые значения более 5:

                   - независимые выборки: тест хи-квадрат.

                   - зависимые выборки: тест МакНемара.

- Непрерывные данные:

       - Непрерывные данные:

                   - Зависимые выборки: знаковый ранговый тест Вилкоксона.

                   - Независимые выборки: тест Манна-Уитни.

 

                                                                                                          

Сравнение 2-х выборок по 1-му признаку

 

А. Параметрические критерии – количественные нормально распределённые данные

Критерий Стьюдента (t-критерий Стьюдента)

t-критерий Стьюдента (псевдоним У. Госсета) является наиболее распространённым параметрическим критерием. Позволяет проверить гипотезу о статистической значимости разности двух арифметических средних в 2-х зависимых или независимых выборках.

Нулевая гипотеза – отсутствие различий средних арифметических значений переменной в двух выборках. В нулевой гипотезе используемая статистика соответствует t-распределению.

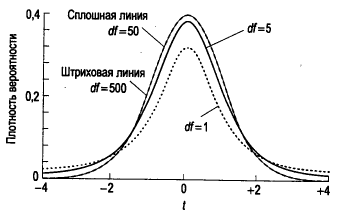
Характеристики t-распределения:

· близко к нормальному, но кривая более приплюснута, с более длинными «хвостами»;

· характеризуется степенями свободы, форма приближается к нормальной по мере увеличения степеней свободы.

 

Требования к выборкам (математические допущения)

· Нормальность распределения переменных в обеих выборках.

· Одинаковость дисперсии (стандартного отклонения).

· Допускается сравнение не более 2-х групп.

· Группы могут большие (n>30), малые или не равными по размеру. Однако, в маленьких выборках трудно установить характер распределения.

t-критерий Стьюдента имеется в 2-х вариантах: для зависимых и для независимых выборок. В статистических программах и калькуляторах используются соответствующие варианты теста.

 

Алгоритм выполнения теста

· Необходимо проверить выборки на нормальность и равенство дисперсий.

· В меню выбирается соответствующий вид теста:

o для зависимых или независимых выборок (парный или непарный тест).

o двусторонний или односторонний.

· Задаётся критический уровень значимости.

· Вводятся варианты.

· Программа рассчитывает число степеней свободы, полученное (расчётное) значение t-критерия и точное значение достигнутого уровня значимости р. В независимых выборках число степеней свободы равно: df =  п_э + п_к - 2, где п_э и п_к - общее число инди­видуальных результатов в 2-х группах. В зависимых выборках df = n – 1, где n – число сопряженных пар.

· Оценка.

o полученное (расчётное, эмпирическое) значение tсравнивается с граничным значением (критическим значением) при 5 %-ном (или другом заданном) уровне значимости (t₀,₀₅) при имеющемся числе степеней свободы. Возможно прямое сравнение достигнутого уровня статистической значимости (р) с критическим.

o Если расчётное tбольше граничного значения, то различия между средними арифметическими двух групп считаются статистически значимыми при 5%-ном уровне значимости (p < a).

o В случае когда полученное t расчётное меньше граничного значения t_0,05, считается, что раз­личия статистически не значимы и разница в среднеарифметических показате­лях групп имеет случайный характер (p > a).

 

В. Сравнение 2-х групп – качественные данные

---

Дата добавления: 2018-04-05; просмотров: 480; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!