Сравнение 2-х независимых групп – критерий хи-квадрат Пирсона
· Назначение. Коэффициент согласия (goodness for fit нет) Пирсона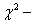 
применяется для проверки эмпирического и теоретического (либо другого эмпирического) распределений одного признака. Применяется в двух случаях:
o Для сопоставления эмпирического распределения признака с теоретическим распределением (нормальным, показательным, равномерным либо каким-то иным законом);
o Для сопоставления двух эмпирических распределений одного и того же признака.
· Нулевая гипотеза Hо: два распределения практически не различаются между собой; альтернативная гипотеза H1: расхождение между распределениями существенно.
· Допущения
o Категориальные данные, шкала наименований.
o Независимые выборки. Данные не зависимы, например пол и привычка курить.
o Частота значений в каждой из клеток не менее 5 (для четырёхпольной таблицы).
· Исходными данными являются частоты, которые вводятся в таблицу сопряжения; четырёхпольная таблица 2 х 2. Частоты являются исходными цифрами, а не процентами.
· Многополосные таблицы (5 х 5 и меньше).
Определение статистической значимости различий данных, измеренных в порядковой (ранговой) шкале
Пример – порядковая шкала с различными баллами в 2-х независимых выборках..
Тест – критерий однородности хи-квадрат.
ЛЕКЦИЯ 8
СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ КОРРЕЛЯЦИОННЫЙ, ДИСПЕРСИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
|
|
|
Содержание
1. Введение. Понятие и виды зависимостей между переменными.
Корреляционный анализ. Виды корреляции.
3. Способы выражения корреляции – корреляционное поле.
4.Способы выражения корреляции – коэффициент корреляции.
5. Регрессионный анализ.
Введение. Понятие и виды зависимостей между переменными
Функциональная и статистическая зависимость
· Функциональная зависимость (взаимосвязь) - каждому значению одной переменной соответствует строго определенное значение другой. Например, в функции у = 2 * х каждому значению х соответствует в два раза большее значение у (определение ускорения по известным данным скорости и т.д.
· Статистическая зависимость –каждому значению одного параметра может соответствовать несколько значений другого; с изменением одного признака изменяется и другой.
Для определения статистической зависимости применяют
· корреляционный и дисперсный анализ - для установления факта наличия/отсутствия зависимости между переменными (характер и силу зависимости)
· регрессионный анализ - для нахождения количественной зависимости между переменными.
Корреляционный анализ. Виды корреляции
|
|
|
Корреляционный анализ – применение статистических методов для исследования взаимосвязи между переменными, т.е. насколько согласованно они меняются. Основной задачей корреляционного анализа является определение тесноты (силы) и направленности статистической зависимости изучаемых показателей. Следует помнить, что корреляция не есть причинность.
Виды корреляции
· По направлению
o Прямая (положительная) -с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого.
o Обратная (отрицательная) -с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого.
· По форме
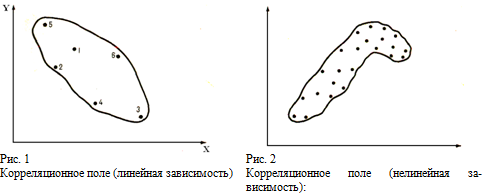
o Линейная- изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину(график представляет прямую линию).
o Нелинейная – любая другая.
Способы выражения корреляции – корреляционное поле
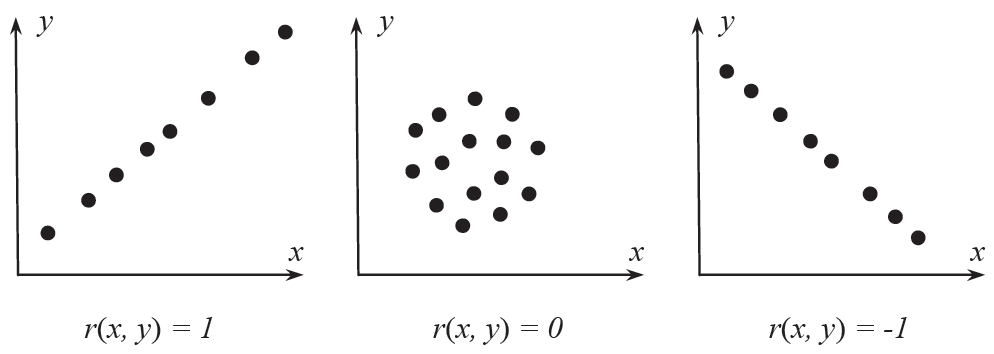
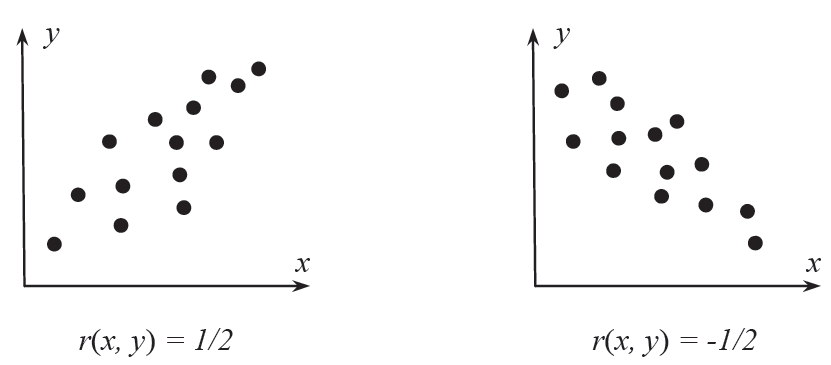
Корреляционное поле (диаграмма рассеивания)
· Графическое представление данных в прямоугольной система координат, при котором каждой паре переменных соответствует одна точка (зона разброса).
· Используется для предварительного визуального анализа корреляционной связи.
|
|
|
· Позволяет оценить наличие корреляции (группировка точек вдоль одной линии), направление корреляции и её силу (по плотности точек).
Дата добавления: 2018-04-05; просмотров: 499; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!