Формула «перемножения» трапеций, формула Симпсона
Рассмотрим интегрирование по способу Симпсона функции, описываемой кубической параболой, приведенной на рис.1.

Рис.1
Формула, которой предлагается пользоваться в этом случае, имеет вид:
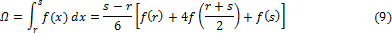
На рис.1 приведены грузовая (а) и единичная (б) эпюры изгибающих моментов для одного участка.

Рис.2
Буквами А, С и В обозначены изгибающие моменты на левом конце участка, посредине и на правом конце участка на грузовой эпюре. Буквами а, c и b обозначены изгибающие моменты на левом конце участка, посредине и на правом конце участка на единичной эпюре.
Интеграл Мора для одного участка имеет вид:

Произведение моментов под интегралом обозначим:

Применяя формулу Симпсона к интегралу Мора после соответствующих замен и подстановок, получим:
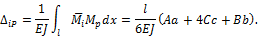
При решении задач с несколькими участками формула Мора-Симпсона принимает вид:

В том случае, если обе эпюры изгибающих моментов, грузовая и единичная, меняются по линейному закону и представляют собой на каждом из участков трапеции, можно исключить средние значения моментов С и с, учитывая, что они могут быть вычислены из выражений:

Подставляя эти значения в формулу (12), получаем формулу трапеций:
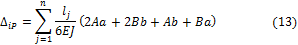
Расчет статически неопределимых стержневых систем
Степень статической неопределенности
Степень статической неопределимости n определяется по формуле:
n=k-m
где,
k – количество неизвестных усилий (реакций связи),
m – количество уравнений равновесия которые можно составить для данной системы.
Системы, для которых n=1 называют однажды статически неопределимыми, n=2 – дважды СН и т.д.
Основная система метода сил
Основной системой метода сил (ОСМС) называется система, образованная из заданной расчётной схемы сооружения удалением лишних связей . Если удаляются все лишние связи, то заданное статически неопределимое сооружение преобразуется в статически определимое. В этом случае, вычислив каким-либо способом реакции в лишних связях от заданных воздействий, мы задачу расчёта статически неопределимого сооружения сведём к известной задаче по определению напряжённо-деформированного состояния в статически определимом сооружении








Основные системы метода сил из заданных статически неопределимых рам можно получить различными способами: удалением опорных связей (рис. 16.1,в; рис. 16.2,в; рис. 16.3,б; рис. 16.4,б), введением простых или кратных цилиндрических шарниров (рис. 16,1,б; рис. 16.3,в; рис. 16.4,в; рис. 16.5,б; рис. 16.7,б), введением поступательных шарниров, как правило, в элементы, имеющие по своим концам цилиндрические шарниры (рис. 16,1,б; рис. 16.2,б,в; рис. 16.7,б,в), удалением всех или части внутренних связей в цилиндрических шарнирах (рис. 16.8,б), разрезом по "живому" сечению (рис. 16.6,в) и другими способами, включая различные сочетания вышеперечисленных.
Для заданной расчётной схемы статически неопределимого сооружения существует множество вариантов основных систем метода сил. Для расчёта принимается вариант, удовлетворяющий ряду требований, среди которых обязательным является требование геометрической неизменяемости основной системы метода сил. С этой точки зрения основные системы метода сил, показанные на рис. 16.1,в и рис. 16.2,в не могут быть использованы для расчёта заданных статически неопределимых рам. Основная система метода сил, изображённая на рис. 16.1,в, по своей структуре геометрически изменяема, так как состоит из двух дисков А и В, соединённых между собой тремя параллельными связями ab, cd, ef одинаковой длины. На рис. 16.2,в показан вариант мгновенно изменяемой основной системы метода сил. Действительно, в этом варианте диск А и диск "земля" В соединяются между собой цилиндрическим шарниром К и связью mn, ось которой проходит через шарнир К.
Выполнение некоторых желательных требований при выборе основной системы метода сил способствует сокращению времени на расчёт статически неопределимого сооружения. Это, прежде всего, образование простых по структуре основных систем методом сил, где чётко просматриваются рабочие схемы (главные и второстепенные части), легко определяются реакции опорных связей и внутренние усилия. С этой точки зрения основная система метода сил, показанная на рис. 16.3,б, предпочтительнее, чем другая основная система (рис. 16.3,в) для этой же рамы.
Важно, чтобы в используемой для расчёта основной системе метода сил эпюры внутренних усилий не "растекались" по всем элементам, т.е. были бы локализованы, и имели бы возможно меньшие по абсолютной величине ординаты. Часто выполнению этого условия способствует введение цилиндрических шарниров в узлы статически неопределимых систем (рис. 16.4,в и рис. 16.6,б).
Для симметричных статически неопределимых сооружений основную систему метода сил следует выбирать также симметричной (рис. 16.6,б,в и рис. 16.7,б).
Дата добавления: 2018-04-04; просмотров: 1182; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
