Касательные напряжения в поперечных сечениях стержня круглого и кольцевого сечений

касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения. При получим . Наибольшие напряжения возникают в точках контура сечения при :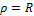

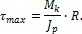
Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления

Для сплошного круглого сечения

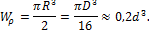
Для кольцевого сечения

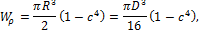
где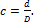

 

Тогда максимальные касательные напряжения равны

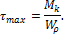
Деформации сдвига и углы закручивания стержня круглого и кольцевого сечений. Расчеты на прочность и жесткость стержня круглого и кольцевого поперечных сечений

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его проч­ности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение, например по формуле (5.9), ;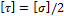

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

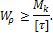
Для сплошного круглого сечения , отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

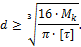
Для кольцевого сечения

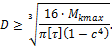
Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания 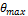, был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

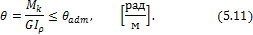
Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

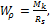но Wp = 0,2d³, поэтому

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

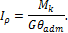
В этой формуле допускаемый относительный угол закручивания 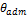должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p будет выглядеть следующим образом:

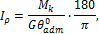
но I_p = 0,1d ⁴ , поэтому

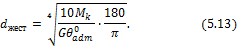
Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d_вн и наружного диаметров d, т.е. при заданном параметре k = d_вн /d, формулы (5.12) и (5.13) принимают вид:

---

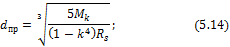
Дата добавления: 2018-04-04; просмотров: 1300; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!