Кинематический анализ сооружений ( стержневых систем)

Геометрически изменяемые, неизменяемые и мгновенно-изменяемые системы

Строительная механика рассматривает геометрически неизменяемые системы (ГНС) (сооружения), то есть такие, перемещения точек которых возможны только в результате деформации системы.

Наипростейшей неизменяемой системой является шарнирный треугольник (рис.1).

Рис.1

Шарнирно-стержневой прямоугольник АВСД, показанный на рис.2, является геометрически изменяемой системой (ГИС), так как приходит в движение без изменения длины и искривления стержней даже при бесконечно малых нагрузках.

Рис.2

Мгновенно изменяемая система (МИС) – система, способная получать лишь мгновенные перемещения (рис. 3).

Рис.3

Кроме уже известных понятий «геометрическая неизменяемость» (и соответственно геометрически неизменяемая система – ГНС), «геометрическая изменяемость» (геометрически изменяемая система – ГИС), «мгновенная изменяемость» (мгновенно изменяемая система – МИС), базовыми понятиями кинематического анализа являются диск, связь и степень свободы.

Степень свободы. Степень статической неопределенности.

Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы в пространстве.

Статически неопределимые системы характеризуются степенью статической неопределимости, которая равна числу «лишних» связей и может быть вычислена как разность между числом неизвестных сил и числом независимых уравнений равновесия. По числу единиц этой разности системы бывают 1,2,3….n раз статически неопределимыми.

Для расчетов составляется силовая схема заданной системы, на которой указываются все известные и неизвестные силовые факторы.

Принципы формирования геометрически неизменяемых систем.

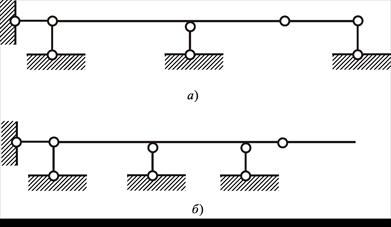
Рис. 1

Так, на Рис.16 системы и имеют одинаковое число дисков, шарниров и опорных стержней, ᴛ.ᴇ. но система действительно неизменяема и неподвижна, а имеет в левой части лишний опорный стержень, а в правой части – одну степень свободы.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, операция определœения числа степеней свободы системы должна быть дополнена анализом геометрической неизменяемости структуры системы.

Простейшие законы образования геометрически неизменяемых систем таковы:

Рис. 2

К двум дискам 1 и 2, связанных друг с другом шарниром присоединœен при помощи шарниров и диск 3, причём прямая не проходит через точку (Рис. 2).

Рис. 3

К диску I (геометрически неизменяемой системе) присоединяется при помощи двух стержней новый узел так, что три шарнира , и не лежат на одной прямой (Рис. 3)

Рис. 4

Два диска (1 и 2) связаны между собой тремя стержнями, оси которых не пересекаются в одной точке (Рис. 4) и не параллельны друг другу.

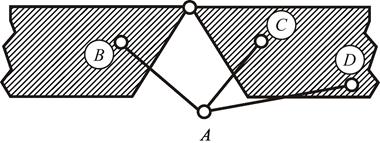
Рис. 5

К геометрически изменяемой фигуре, имеющей одну степень изменяемости, шарнирно присоединяется новая точка тремя стержнями (Рис. 5), причём все три шарнира , и не принадлежат к одному и тому же звену.

Дата добавления: 2018-04-04; просмотров: 920; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12 13 14 15 161718 19 20 21 Следующая ⇒

Мы поможем в написании ваших работ!